机器学习：5.线性回归算法

1.本节重点知识点用自己的话总结出来，可以配上图片，以及说明该知识点的重要性

　　在本节课主要学习了线性回归算法，理解了算法的定义：线性回归是基于已有数据对未知的数据进行预测的。比如：①房价预测，如图1-1、数据可视化如图1-2；

图1-1 通过房面积来预测价格

图1-2 画出面积与房价的线性关系图

②销售额预测，如图1-3；

图1-3 通过历年销售额来预测

③额度贷款预测，如图1-4。等等。。。

图1-4 根据个人诚信度对贷款额度进行预测

线性回归算法优缺点：

优点：

　　①思想简单，实现容易。建模迅速，对于小数据量、简单的关系很有效；

　　②是许多强大的非线性模型的基础。

　　③线性回归模型十分容易理解，结果具有很好的可解释性，有利于决策分析。

　　④蕴含机器学习中的很多重要思想。

　　⑤能解决回归问题。

缺点：

　　①对于非线性数据或者数据特征间具有相关性多项式回归难以建模.

　　②难以很好地表达高度复杂的数据。

 

机器预测和真实值也是有一定的误差的，那就需要利用算法尽量减少误差比如：正规方程、梯度下降法。

 

 

方法一：正规方程

方法二：梯度下降

2.思考线性回归算法可以用来做什么？

　　课堂实例：房价预测、销售额预测、额度贷款预测

PS：生活中还有许多可以利用线性回归算法来预测未知数据的实例：

　　①预测天气情况；

　　②企业的销售收入与广告支出的预测；

　　③根据某地犯案情况预测犯罪率

 

3.自主编写线性回归算法 ，数据可以自己造，或者从网上获取。（加分题）

 算法案例：预测商品的销售额。

　　详情：商品的销售额可能因电视、广播、报纸等广告投入的关系而受影响，分析这些因素来预测商品的销售额。

　　数据来源：　　

　　　　链接：https://pan.baidu.com/s/1DY8SQ7AZZDnHQM-HCbSn6w
　　　　提取码：f1im

 　　部分数据截图：

 实现代码如下：

import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
import pandas as pd
from sklearn.linear_model import LinearRegression
import numpy as np
plt.rcParams['font.sans-serif'] = 'SimHei'  # 设置中文显示
# 读取数据
data = pd.read_csv('../data/advertising.csv')
# data = pd.read_csv('./machine_learning/data/advertising.csv')
df = pd.DataFrame(data)

# 数据预处理
# 选择特征列表
df1 = df[['TV', 'radio', 'newspaper']]
df2 = df['sales']
# 选择DataFrame-df的子集
X = df1
y = df2
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=6, test_size=0.2)  # 分为训练集和测试集，训练集占0.8

# 训练模型
Lrn = LinearRegression()  # 尝试了下不能直接使用LinearRegression()来进行拟合
Lrn_model = Lrn.fit(X_train, y_train)
print('截距项：', Lrn_model.intercept_)
print('回归系数：', Lrn_model.coef_)
# 预测结果
Lrn_pre = Lrn.predict(X_test)
print("预测结果:", Lrn_pre)
# 测试准确度
print('\n模型的准确率：', Lrn_model.score(X_test, y_test))

# 绘制ROC曲线
plt.figure(figsize=(8, 6))  # 创建一个画布
plt.plot(range(len(Lrn_pre)), Lrn_pre, 'b', label='预测值:Lrn_pre')
plt.plot(range(len(y_test)), y_test, 'r', label='真实值:y_test')
# 显示图中的标签
plt.legend()
plt.title("预测值与真实值的ROC曲线")
plt.xlabel('销售量')  # 横坐标
plt.ylabel('销售额')  # 纵坐标
plt.show()

测试结果如下：

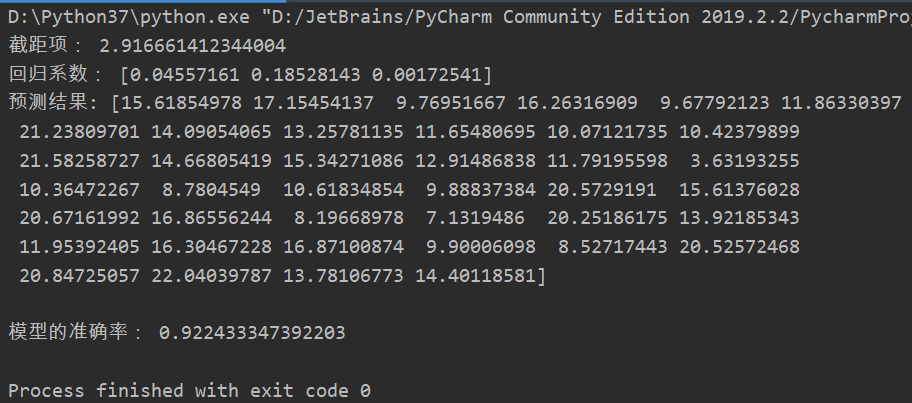
 可以看出这个数据训练出来的准确率是很高了，证明预测出来的结果误差很小。模型的三个回归系数分别对应：TV、radio、newspaper，TV的回归系数最大，说明TV对商品的销售额影响最大。

 

ROC曲线图：

 

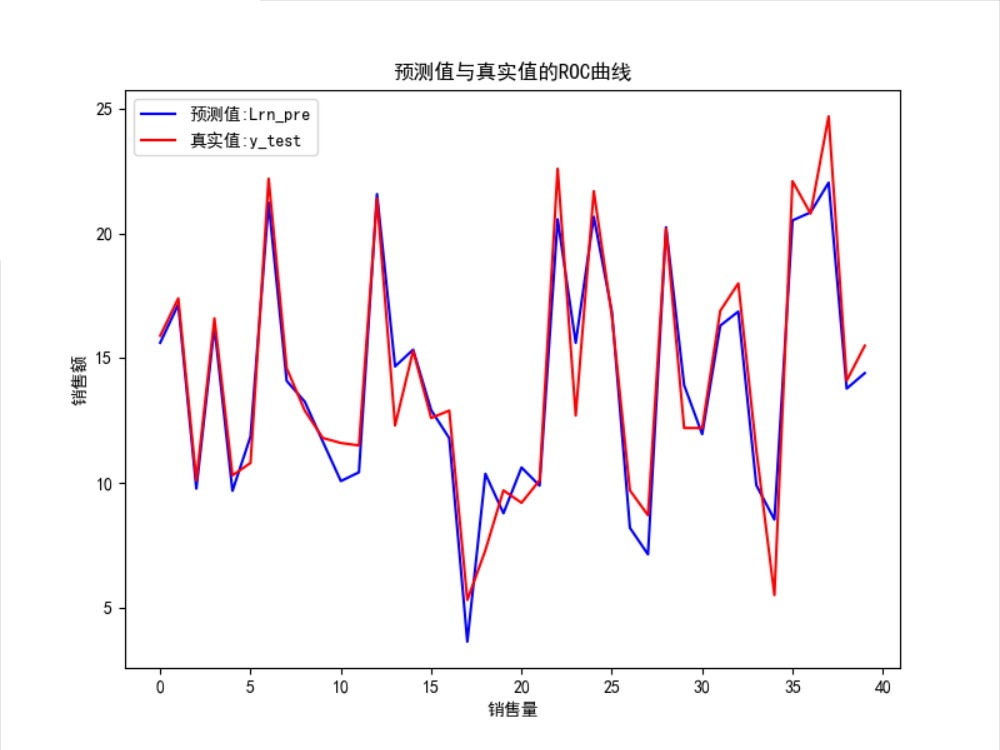
从上图可以看模型的测试集的预测的出的结果(Lrn_pre)与真实的测试值(y_test)误差很小，说明整个数据拟合出的模型还是很不错，不过也是因为训练模型的数据以及所考虑的影响因素不够多的原因。