SOS DP学习笔记

Sum over Subsets(SOS) DP

一、引入

给出一个长度为\(2^n\)的数组\(A\)，对于每一个\(mask< 2^n\)要求计算出\(f[mask]=\sum_{sub\in mask}A[sub]\)
(其中\(sub\in mask\)表示\(sub\&mask=sub\))

二、解法

1.暴力

for(int mask = 0; mask < (1<<n); mask++)
    for(int sub = 0; sub <= mask; sub++)
        if((sub & mask) == sub)
            f[mask] += A[sub];

根据定义直接做，枚举所有小于\(mask\)的集合，判断\(sub\)是否是\(mask\)的子集

复杂度\(O(4^n)\)

2.子集枚举

for(int mask = 0; mask < (1<<n); mask++){
    for(int sub = mask; ; sub = mask&(sub-1)){
        f[mask] += A[sub];
        if(!sub) break;
    }
}

子集枚举优化之后
总复杂度是\(\sum_{m=0}^{n}C(n,m)\cdot 2^m = \sum_{m=0}^{n}C(n,m)\cdot 2^m\cdot 1^{n-m}=(1+2)^n\)
复杂度\(O(3^n)\)

3.SOSDP

考虑在计算当前的状态的\(f[mask]\)的时候，能否利用之前计算的结果来优化复杂度，并且不会重复计算
那就要定义新的状态：\(f[mask][bit]\)表示对于集合\(mask\)，在子集\(sub\)和\(mask\)只有最后\(bit\)位存在不同的情况下的答案
可以发现\(f[mask][bit]= \begin{cases} A[mask] & bit=-1 \\ f[mask][bit-1] & mask\&(1<<bit)=0 \\ f[mask][bit-1]+f[mask \bigoplus (1<<bit)][bit-1] & mask\&(1<<bit)!=0 \end{cases}\)

当前位是\(1\)的情况下有两个分支，这个位置是\(1\)或者\(0\)，并且从只改变之后的位的状态转移过来，能保证不重复
当前位是\(0\)的情况下这个位不能改变，所以只能选这位是\(0\)的之后的状态转换过来

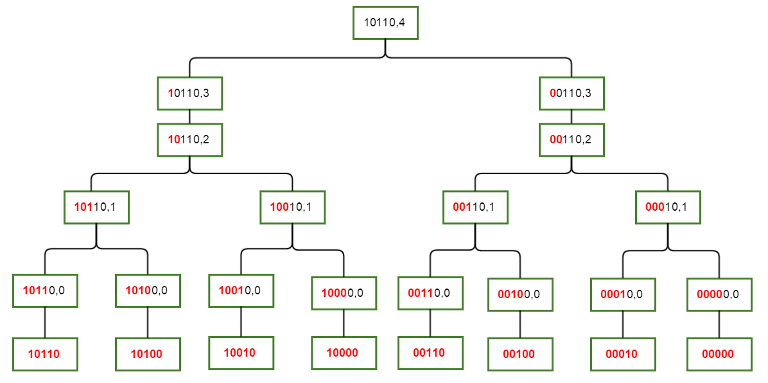
空间压缩一下，代码如下

for(int mask = 0; mask < (1<<n); mask++) f[mask] = A[mask];
for(int bit = 0; bit < n; bit++)
    for(int mask = 0; mask < (1<<n); mask++)
        if(mask&(1<<bit)) f[mask] += f[mask^(1<<bit)];

复杂度\(O(n2^n)\)

考虑一下如何计算\(f[sub]=\sum_{sub \in mask} A[mask]\)

可以发现把所有集合取反，\(f[\overline{sub}] = \sum_{\overline{mask}\in \overline{sub}}A[\overline{mask}]\)
就相当于把\(0\)变成\(1\)来处理，代码基本相同

for(int mask = 0; mask < (1<<n); mask++) f[mask] = A[mask];
for(int bit = 0; bit < n; bit++)
    for(int mask = 0; mask < (1<<n); mask++)
        if(!(mask&(1<<bit))) f[mask] += f[mask^(1<<bit)];            // 只有这里的if改了

三、例题

1. Codeforces165E 🔗 代码
2. Codeforces383E 🔗 代码
3. Codeforces449D 🔗 代码
4. Codeforces1208F 🔗 代码
5. Hdu5977 🔗 代码

参考CF博客🔗