ACM-ICPC 2018 焦作赛区网络预赛
\(A. Magic Mirror\)
签到
//#pragma GCC optimize("O3")
//#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<bits/stdc++.h>
using namespace std;
int main(){
int T;
for(cin >> T; T; T--){
string s;
cin >> s;
for(int i = 0; i < (int)s.length(); i++) s[i] = tolower(s[i]);
if(s=="jessie") cout << "Good guy!" << endl;
else cout << "Dare you say that again?" << endl;
}
return 0;
}
\(B. Mathematical Curse\)
\(dp[i][j]\)表示当前到第\(i\)个巫师,消除标记到\(j\)的最大值和最小值
因为有正有负,两个负数相乘变成正数可能变化比较大,所以要存正负的极值
//#pragma GCC optimize("O3")
//#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<bits/stdc++.h>
using namespace std;
function<void(void)> ____ = [](){ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0);};
const int MAXN = 1111;
using LL = int_fast64_t;
const LL INF = 0x3f3f3f3f3f3f3f3f;
LL ope(LL x, char op, LL y){
if(op=='-') return x - y;
if(op=='+') return x + y;
if(op=='*') return x * y;
return x / y;
}
char s[MAXN];
LL f[2][MAXN][6];
int n,m,A[MAXN],K;
void solve(){
cin >> n >> m >> K;
memset(f[0],0x3f,sizeof(f[0]));
memset(f[1],-0x3f,sizeof(f[1]));
for(int i = 0; i <= n; i++) f[0][i][0] = f[1][i][0] = K;
for(int i = 1; i <= n; i++) cin >> A[i];
cin >> (s+1);
for(int i = 1; i <= n; i++) for(int j = 1; j <= min(i,m); j++){
f[0][i][j] = f[0][i-1][j];
f[1][i][j] = f[1][i-1][j];
if(f[0][i-1][j-1]!=INF){
f[0][i][j] = min(f[0][i][j],ope(f[0][i-1][j-1],s[j],A[i]));
f[1][i][j] = max(f[1][i][j],ope(f[0][i-1][j-1],s[j],A[i]));
}
if(f[1][i-1][j-1]!=-INF){
f[0][i][j] = min(f[0][i][j],ope(f[1][i-1][j-1],s[j],A[i]));
f[1][i][j] = max(f[1][i][j],ope(f[1][i-1][j-1],s[j],A[i]));
}
}
LL ret = -INF;
for(int i = m; i <= n; i++) ret = max(ret,f[1][i][m]);
cout << ret << endl;
}
int main(){
int T;
____();
for(cin >> T; T; T--) solve();
return 0;
}
\(C. Password\)
\(D. Sequence\)
\(E. Jiu Yuan Wants to Eat\)
如果只有\(1,2,4\)操作那就是树剖的模板题了,现在多了一个操作\(3\)
其实还是模板题,因为是对\(2^{64}\)取模,那么每个数按位取反就相当于每个数被\(2^{64}-1\)减,那就相当于每个数先减去\(2^{64}-1\)然后再取负,那么这题就出来了
//#pragma GCC optimize("O3")
//#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<bits/stdc++.h>
using namespace std;
function<void(void)> ____ = [](){ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0);};
using ull = uint_fast64_t;
const int MAXN = 1e5+7;
struct SegmentTree{
ull w[MAXN<<2],lmul[MAXN<<2],ladd[MAXN<<2];
int l[MAXN<<2],r[MAXN<<2];
#define ls(rt) rt << 1
#define rs(rt) rt << 1 | 1
#define pushup(rt) w[rt] = w[ls(rt)] + w[rs(rt)]
void build(int L, int R, int rt = 1){
l[rt] = L, r[rt] = R; w[rt] = 0ull;
lmul[rt] = 1ull; ladd[rt] = 0ull;
if(L+1==R) return;
int mid = (L + R) >> 1;
build(L,mid,ls(rt)); build(mid,R,rs(rt));
}
void pushdown(int rt){
if(lmul[rt]!=1ull){
lmul[ls(rt)] *= lmul[rt]; ladd[ls(rt)] *= lmul[rt]; w[ls(rt)] *= lmul[rt];
lmul[rs(rt)] *= lmul[rt]; ladd[rs(rt)] *= lmul[rt]; w[rs(rt)] *= lmul[rt];
lmul[rt] = 1ull;
}
if(ladd[rt]){
ladd[ls(rt)] += ladd[rt];
ladd[rs(rt)] += ladd[rt];
w[ls(rt)] += ladd[rt] * (r[ls(rt)] - l[ls(rt)]);
w[rs(rt)] += ladd[rt] * (r[rs(rt)] - l[rs(rt)]);
ladd[rt] = 0ull;
}
}
void update(int L, int R, int op, ull x, int rt = 1){
if(l[rt]>=R or L>=r[rt]) return;
if(L<=l[rt] and r[rt]<=R){
if(op==3){
w[rt] -= -1ull * (r[rt] - l[rt]);
ladd[rt] -= -1ull;
w[rt] = -w[rt], lmul[rt] = -lmul[rt], ladd[rt] = -ladd[rt];
}
else if(op==2) w[rt] += x * (r[rt] - l[rt]), ladd[rt] += x;
else if(op==1) w[rt] *= x, ladd[rt] *= x, lmul[rt] *= x;
return;
}
pushdown(rt);
update(L,R,op,x,ls(rt)); update(L,R,op,x,rs(rt));
pushup(rt);
}
ull qsum(int L, int R, int rt = 1){
if(l[rt]>=R or L>=r[rt]) return 0;
if(L<=l[rt] and r[rt]<=R) return w[rt];
pushdown(rt);
return qsum(L,R,ls(rt)) + qsum(L,R,rs(rt));
}
}ST;
int n,m,dfn[MAXN],num,tp[MAXN],sz[MAXN],son[MAXN],depth[MAXN],par[MAXN];
vector<int> G[MAXN];
void dfs1(int u){
depth[u] = depth[par[u]] + 1;
sz[u] = 1; son[u] = 0;
for(int v : G[u]){
dfs1(v);
sz[u] += sz[v];
if(sz[son[u]]<sz[v]) son[u] = v;
}
}
void dfs2(int u, int top){
tp[u] = top;
dfn[u] = ++num;
if(son[u]) dfs2(son[u],top);
for(int v : G[u]){
if(v==son[u]) continue;
dfs2(v,v);
}
}
void modify(int u, int v, int op, ull x = 0ull){
while(tp[u]!=tp[v]){
if(depth[tp[u]]<depth[tp[v]]) swap(u,v);
ST.update(dfn[tp[u]],dfn[u]+1,op,x);
u = par[tp[u]];
}
if(depth[u]<depth[v]) swap(u,v);
ST.update(dfn[v],dfn[u]+1,op,x);
}
ull qsum(int u, int v){
ull ret = 0;
while(tp[u]!=tp[v]){
if(depth[tp[u]]<depth[tp[v]]) swap(u,v);
ret += ST.qsum(dfn[tp[u]],dfn[u]+1);
u = par[tp[u]];
}
if(depth[u]<depth[v]) swap(u,v);
return ret + ST.qsum(dfn[v],dfn[u]+1);
}
int main(){
while(scanf("%d",&n)!=EOF){
num = 0;
for(int i = 1; i <= n; i++) G[i].clear();
for(int i = 2; i <= n; i++){
scanf("%d",&par[i]);
G[par[i]].push_back(i);
}
dfs1(1); dfs2(1,1);
ST.build(1,n+1);
scanf("%d",&m);
while(m--){
int op; scanf("%d",&op);
if(op<=2){
int u, v; ull x;
scanf("%d %d %llu",&u,&v,&x);
modify(u,v,op,x);
}
else if(op==3){
int u, v;
scanf("%d %d",&u,&v);
modify(u,v,op);
}
else{
int u, v;
scanf("%d %d",&u,&v);
printf("%llu\n",qsum(u,v));
}
}
}
return 0;
}
\(F. Modular Production Line\)
K次区间覆盖问题,边权取负最小费用流
//#pragma GCC optimize("O3")
//#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<bits/stdc++.h>
using namespace std;
function<void(void)> ____ = [](){ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0);};
const int MAXN = 1111;
const int INF = 0x3f3f3f3f;
#define S 0
#define T MAXN - 1
int k,m,n,flow[MAXN],dist[MAXN],pre[MAXN],preid[MAXN],vis[MAXN];
pair<pair<int,int>,int> work[MAXN];
struct EDGE{
int to,cap,fee,rev;
EDGE(){}
EDGE(int _to, int _cap, int _fee, int _rev){
to = _to; cap = _cap;
fee = _fee; rev = _rev;
}
};
vector<EDGE> G[MAXN];
void ADDEDGE(int u, int v, int cap, int fee){
G[u].emplace_back(EDGE(v,cap,fee,(int)G[v].size()));
G[v].emplace_back(EDGE(u,0,-fee,(int)G[u].size()-1));
}
void build(){
for(int i = 0; i < MAXN; i++) G[i].clear();
for(int i = 0; i < n; i++) ADDEDGE(i,i+1,k,0);
ADDEDGE(n,T,k,0);
for(int i = 1; i <= m; i++) ADDEDGE(work[i].first.first,work[i].first.second,1,-work[i].second);
}
bool spfa(){
memset(dist,0x3f,sizeof(dist));
dist[S] = 0;
flow[S] = INF;
memset(vis,0,sizeof(vis));
queue<int> que;
que.push(S);
while(!que.empty()){
int u = que.front();
que.pop();
vis[u] = 0;
for(int i = 0; i < (int)G[u].size(); i++){
auto e = G[u][i];
if(!e.cap or dist[e.to]<=dist[u]+e.fee) continue;
dist[e.to] = dist[u] + e.fee;
flow[e.to] = min(e.cap,flow[u]);
pre[e.to] = u; preid[e.to] = i;
if(!vis[e.to]){
vis[e.to] = 1;
que.push(e.to);
}
}
}
return dist[T]!=INF;
}
int mcmf(){
int cost = 0;
while(spfa()){
int u = T;
cost += dist[T] * flow[T];
while(u!=S){
int p = pre[u], id = preid[u];
G[p][id].cap -= flow[T];
G[u][G[p][id].rev].cap += flow[T];
u = pre[u];
}
}
return cost;
}
void solve(){
cin >> n >> k >> m;
vector<int> vec;
for(int i = 1; i <= m; i++){
cin >> work[i].first.first >> work[i].first.second >> work[i].second;
work[i].first.second++;
vec.push_back(work[i].first.first); vec.push_back(work[i].first.second);
}
sort(vec.begin(),vec.end());
vec.erase(unique(vec.begin(),vec.end()),vec.end());
for(int i = 1; i <= m; i++){
work[i].first.first = lower_bound(vec.begin(),vec.end(),work[i].first.first) - vec.begin() + 1;
work[i].first.second = lower_bound(vec.begin(),vec.end(),work[i].first.second) - vec.begin() + 1;
}
n = vec.size();
build();
cout << -mcmf() << endl;
}
int main(){
int t;
____();
for(cin >> t; t; t--) solve();
return 0;
}
\(G. Give Candies\)
计算\(2^n\),利用费马小定理降幂,然后快速幂
//#pragma GCC optimize("O3")
//#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<bits/stdc++.h>
using namespace std;
void ____(){ ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0); }
const int MAXN = 2e5+7;
typedef long long int LL;
const LL MOD = 1e9+7;
char s[MAXN];
LL qpow(LL a, LL b){
LL ret = 1;
while(b){
if(b&1) ret = ret * a % MOD;
b >>= 1;
a = a * a % MOD;
}
return ret;
}
void solve(){
cin >> s;
LL pw = 0;
for(int i = 0, len = strlen(s); i < len; i++) pw = (pw*10+s[i]-'0')%(MOD-1);
pw = (pw-1+MOD)%MOD;
cout << qpow(2,pw) << endl;
}
int main(){
____();
int T;
for(cin >> T; T; T--) solve();
return 0;
}
\(H. String and Times\)
SAM,找\(right\)集合大小在\([L,R]\)的子串有多少个
//#pragma GCC optimize("O3")
//#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<bits/stdc++.h>
using namespace std;
function<void(void)> ____ = [](){ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0);};
const int MAXN = 4e5+7;
struct SAM{
int tot,ch[MAXN][26],link[MAXN],last,cnt[MAXN],c[MAXN],sa[MAXN],len[MAXN];
void clear(){ last = tot = 1; memset(ch[tot],0,sizeof(ch[tot])); link[1] = 0; cnt[1] = 0; }
int newnode(){ tot++; memset(ch[tot],0,sizeof(ch[tot])); cnt[tot] = 0; return tot; }
void extend(char car){
int c = car - 'A';
int np = newnode(), p = last;
len[np] = len[last] + 1; cnt[np] = 1;
while(p and !ch[p][c]){
ch[p][c] = np;
p = link[p];
}
if(!p) link[np] = 1;
else{
int q = ch[p][c];
if(len[p]+1==len[q]) link[np] = q;
else{
int clone = newnode();
link[clone] = link[q];
memcpy(ch[clone],ch[q],sizeof(ch[q]));
len[clone] = len[p] + 1;
while(p and ch[p][c]==q){
ch[p][c] = clone;
p = link[p];
}
link[q] = link[np] = clone;
}
}
last = np;
}
long long int query(int L, int R){
for(int i = 0; i <= tot; i++) c[i] = 0;
for(int i = 1; i <= tot; i++) c[len[i]]++;
for(int i = 1; i <= tot; i++) c[i] += c[i-1];
for(int i = tot; i >= 1; i--) sa[c[len[i]]--] = i;
for(int i = tot; i >= 1; i--){
int u = sa[i];
cnt[link[u]] += cnt[u];
}
long long int ret = 0;
for(int i = 2; i <= tot; i++) if(cnt[i]>=L and cnt[i]<=R) ret += len[i] - len[link[i]];
return ret;
}
}sam;
char s[MAXN];
int main(){
while(scanf("%s",s)!=EOF){
int l, r;
scanf("%d %d",&l,&r);
sam.clear();
for(int i = 0, len = strlen(s); i < len; i++) sam.extend(s[i]);
printf("%lld\n",sam.query(l,r));
}
return 0;
}
\(I. Save the Room\)
签到
//#pragma GCC optimize("O3")
//#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<bits/stdc++.h>
using namespace std;
int main(){
int a,b,c;
while(cin >> a >> b >> c){
if((a&1) and (b&1) and (c&1)) cout << "No" << endl;
else cout << "Yes" << endl;
}
return 0;
}
\(J. Participate in E-sports\)
\(K. Transport Ship\)
二进制拆解+完全背包
//#pragma GCC optimize("O3")
//#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<bits/stdc++.h>
using namespace std;
function<void(void)> ____ = [](){ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0);};
typedef long long int LL;
const int MAXN = 1e4+7;
const LL MOD = 1e9+7;
int n,q,Q[MAXN],f[MAXN];
vector<int> vec;
void solve(){
scanf("%d %d",&n,&q);
vec.clear();
for(int i = 1; i <= n; i++){
int v, c;
scanf("%d %d",&v,&c);
c = (1<<c) - 1;
for(int bit = 0; c&(1<<bit); bit++) vec.emplace_back(v*(1<<bit));
}
memset(f,255,sizeof(f));
for(int i = 1; i <= q; i++) scanf("%d",&Q[i]);
int maxx = *max_element(Q+1,Q+1+q);
f[0] = 1;
for(int p : vec){
for(int i = maxx; i >= p; i--){
if(f[i-p]!=-1){
if(f[i]==-1) f[i] = f[i-p];
else f[i] = (f[i]+f[i-p])%MOD;
}
}
}
for(int i = 1; i <= q; i++) printf("%d\n",(f[Q[i]]==-1?0:f[Q[i]]));
}
int main(){
int T;
for(scanf("%d",&T); T; T--) solve();
return 0;
}
\(L. Poor God Water\)
矩阵快速幂优化DP
把三种东西看作\(A,B,C\),然后两两组合,构造一个\(9\cdot 9\)的矩阵来求解
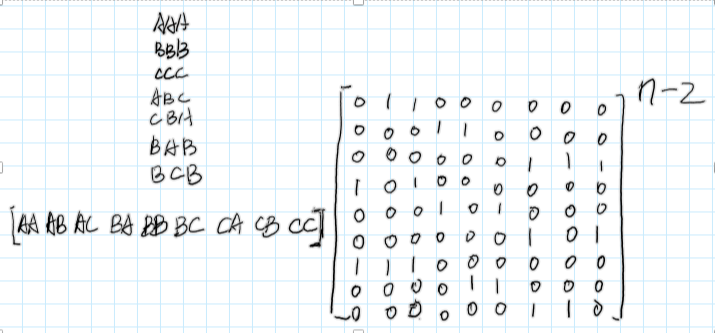
//#pragma GCC optimize("O3")
//#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<bits/stdc++.h>
using namespace std;
void ____(){ ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0); }
typedef long long int LL;
const LL MOD = 1e9+7;
struct Matrix{
LL m[9][9];
Matrix(int tag = 0){
for(int i = 0; i < 9; i++) for(int j = 0; j < 9; j++){
if(i==j) m[i][j] = tag;
else m[i][j] = 0;
}
}
void set(int x, int y){ m[x][y] = 1; }
Matrix operator * (const Matrix rhs){
Matrix ret(0);
for(int i = 0; i < 9; i++) for(int j = 0; j < 9; j++){
for(int k = 0; k < 9; k++) ret.m[i][j] = (ret.m[i][j] + m[i][k] * rhs.m[k][j]) %MOD;
}
return ret;
}
};
Matrix qpow(Matrix A, LL b){
Matrix ret(1);
while(b){
if(b&1) ret = ret * A;
b >>= 1;
A = A * A;
}
return ret;
}
LL n;
Matrix init(0);
void solve(){
cin >> n;
if(n==1){
cout << 3 << endl;
return;
}
Matrix ret = qpow(init,n-2);
LL res = 0;
for(int i = 0; i < 9; i++) for(int j = 0; j < 9; j++) res = (res + ret.m[i][j]) % MOD;
cout << res << endl;
}
int main(){
____();
init.set(0,1); init.set(0,2);
init.set(1,3); init.set(1,4);
init.set(2,6); init.set(2,7); init.set(2,8);
init.set(3,0); init.set(3,2);
init.set(4,3); init.set(4,5);
init.set(5,6); init.set(5,8);
init.set(6,0); init.set(6,1); init.set(6,2);
init.set(7,4); init.set(7,5);
init.set(8,6); init.set(8,7);
int T; for(cin >> T; T; T--) solve();
return 0;
}

