2019-2020 ACM-ICPC Brazil Subregional Programming Contest (11/13)
\(2019-2020\ ACM-ICPC\ Brazil\ Subregional\ Programming\ Contest\)
\(A.Artwork\)
并查集,把检测区域能在一起的检测器放在一个并查集里,然后判断是否有一个集合能够封住左边和上边的其中一个还有右边和下边的其中一个即可
//#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<bits/stdc++.h>
using namespace std;
function<void(void)> ____ = [](){ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0);};
const int MAXN = 1111;
const int INF = 0x3f3f3f3f;
int n,m,k,root[MAXN],tot;
pair<pair<int,int>,int> sensor[MAXN];
vector<int> SET[MAXN];
map<int,int> mp;
int findx(int x){
if(x!=root[x]) root[x] = findx(root[x]);
return root[x];
}
int dist(const pair<int,int> &A, const pair<int,int> &B){
return (A.first-B.first)*(A.first-B.first)+(A.second-B.second)*(A.second-B.second);
}
int main(){
scanf("%d %d %d",&n,&m,&k);
for(int i = 1; i <= k; i++) scanf("%d %d %d",&sensor[i].first.first,&sensor[i].first.second,&sensor[i].second);
for(int i = 1; i <= k; i++) root[i] = i;
for(int i = 1; i <= k; i++) for(int j = i+1; j <= k; j++){
int fa = findx(i);
int fb = findx(j);
if(fa==fb) continue;
if((sensor[i].second+sensor[j].second)*(sensor[i].second+sensor[j].second)>=dist(sensor[i].first,sensor[j].first)){
root[fa] = fb;
}
}
for(int i = 1; i <= k; i++){
if(!mp.count(findx(i))) mp.insert(make_pair(findx(i),++tot));
SET[mp.at(findx(i))].emplace_back(i);
}
bool ok = true;
for(int i = 1; i <= tot; i++){
int u = -INF, d = INF, l = INF, r = -INF;
for(auto p : SET[i]){
u = max(u,sensor[p].first.second+sensor[p].second);
d = min(d,sensor[p].first.second-sensor[p].second);
l = min(l,sensor[p].first.first-sensor[p].second);
r = max(r,sensor[p].first.first+sensor[p].second);
}
if((u>=m||l<=0)&&(d<=0||r>=n)){
ok = false;
break;
}
}
puts(ok?"S":"N");
return 0;
}
\(B.Buffoon\)
签到
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+10;
int a[N],n,maxi;
int main(){
cin>>n;
for(int i=1;i<=n;++i) cin >> a[i], maxi = max(maxi,a[i]);
if(maxi==a[1]) cout << "S";
else cout << "N";
return 0;
}
\(C.Crossings\ With\ Danger\)
\(D.Denouncing Mafia\)
树形DP+优先队列 对于每个节点记录它的最深节点的位置,把链长为关键字丢到优先队列中,每次找最长的没有被遍历过的链
//#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<bits/stdc++.h>
using namespace std;
function<void(void)> ____ = [](){ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0);};
const int MAXN = 1e5+7;
int n,m,par[MAXN],depth[MAXN],vis[MAXN];
vector<int> G[MAXN];
priority_queue<pair<int,pair<int,int>>,vector<pair<int,pair<int,int>>>,less<pair<int,pair<int,int>>>> que;
int dfs(int u){
depth[u] = depth[par[u]]+1;
int maxdep = u;
for(int v : G[u]){
int p = dfs(v);
maxdep = depth[maxdep]<depth[p]?p:maxdep;
}
que.push(make_pair(depth[maxdep]-depth[u]+1,make_pair(maxdep,u)));
return maxdep;
}
int main(){
scanf("%d %d",&n,&m);
for(int i = 2; i <= n; i++){
scanf("%d",&par[i]);
G[par[i]].emplace_back(i);
}
dfs(1);
int ans = 0;
while(!que.empty()&&m){
auto p = que.top();
que.pop();
if(vis[p.second.second]) continue;
m--;
ans += p.first;
while(p.second.first!=par[p.second.second]){
vis[p.second.first] = 1;
p.second.first = par[p.second.first];
}
}
printf("%d\n",ans);
return 0;
}
\(E.Exhibition\ of\ Clownfish\)
\(F.Forests\ in\ Danger\)
二分河流宽度,然后得到的矩形先和大矩形求交,再把所有矩形求面积并即可
//#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<bits/stdc++.h>
using namespace std;
function<void(void)> ____ = [](){ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0);};
using LL = int_fast64_t;
const int MAXN = 1e5+7;
struct Rectangle{
int x1,y1,x2,y2;
Rectangle (int _x1 = 0, int _y1 = 0, int _x2 = 0, int _y2 = 0){
x1 = _x1; y1 = _y1;
x2 = _x2; y2 = _y2;
}
Rectangle intersect(const Rectangle &rhs){
int nx1 = max(x1,rhs.x1);
int ny1 = max(y1,rhs.y1);
int nx2 = min(x2,rhs.x2);
int ny2 = min(y2,rhs.y2);
return Rectangle(nx1,ny1,nx2,ny2);
}
}river[MAXN],Forest;
vector<pair<pair<int,int>,int> > line[MAXN];
int n,p;
struct SegmentTree{
int sz[MAXN<<2],cover[MAXN<<2],l[MAXN<<2],r[MAXN<<2];
#define ls(rt) rt << 1
#define rs(rt) rt << 1 | 1
void pushup(int rt){
if(l[rt]+1==r[rt]){
if(cover[rt]) sz[rt] = 1;
else sz[rt] = 0;
return;
}
if(cover[rt]) sz[rt] = r[rt] - l[rt];
else sz[rt] = sz[ls(rt)] + sz[rs(rt)];
}
void build(int L, int R, int rt){
l[rt] = L, r[rt] = R;
sz[rt] = cover[rt] = 0;
if(L+1==R) return;
int mid = (L+R) >> 1;
build(L,mid,ls(rt));
build(mid,R,rs(rt));
}
void update(int L, int R, int rt, int x){
if(l[rt]>=R || L>=r[rt]) return;
if(L<=l[rt] && r[rt]<=R){
cover[rt] += x;
pushup(rt);
return;
}
update(L,R,ls(rt),x);
update(L,R,rs(rt),x);
pushup(rt);
}
int query(){ return sz[1]; }
}ST;
bool check(int mid){
for(int i = 0; i < MAXN; i++) line[i].clear();
for(int i = 1; i <= n; i++){
Rectangle tp(river[i].x1-mid,river[i].y1-mid,river[i].x2+mid,river[i].y2+mid);
tp = tp.intersect(Forest);
line[tp.y1].emplace_back(make_pair(make_pair(tp.x1,tp.x2),1));
line[tp.y2].emplace_back(make_pair(make_pair(tp.x1,tp.x2),-1));
}
LL area = 0;
ST.build(0,Forest.x2+1,1);
for(int i = Forest.y1; i <= Forest.y2; i++){
area += ST.query();
for(auto p : line[i]) ST.update(p.first.first,p.first.second,1,p.second);
}
return area*100 >= (LL(Forest.x2)-Forest.x1)*(Forest.y2-Forest.y1)*p;
}
int solve(){
int l = 1, r = MAXN;
while(l<=r){
int mid = (l+r) >> 1;
if(check(mid)) r = mid - 1;
else l = mid + 1;
}
return l;
}
int main(){
scanf("%d",&n);
for(int i = 1; i <= n; i++){
scanf("%d %d %d %d",&river[i].x1,&river[i].y1,&river[i].x2,&river[i].y2);
if(river[i].x1>river[i].x2) swap(river[i].x1,river[i].x2);
if(river[i].y1>river[i].y2) swap(river[i].y1,river[i].y2);
}
scanf("%d",&p);
scanf("%d %d %d %d",&Forest.x1,&Forest.y1,&Forest.x2,&Forest.y2);
if(Forest.x1>Forest.x2) swap(Forest.x1,Forest.x2);
if(Forest.y1>Forest.y2) swap(Forest.y1,Forest.y2);
printf("%d\n",solve());
return 0;
}
\(G.Getting\ Confidence\)
将乘法变成对数的加法然后就是KM匹配的模板了
//#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<bits/stdc++.h>
using namespace std;
function<void(void)> ____ = [](){ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0);};
const int MAXN = 111;
const int INF = 0x3f3f3f3f;
int n,LX[MAXN],LY[MAXN],visx[MAXN],visy[MAXN],match[MAXN],slack[MAXN],G[MAXN][MAXN];
bool dfs(int x){
visx[x] = 1;
for(int y = 1; y <= n; y++){
if(visy[y]) continue;
int gap = LX[x] + LY[y] - G[x][y];
if(!gap){
visy[y] = 1;
if(match[y]==-1||(!visx[match[y]]&&dfs(match[y]))){
match[y] = x;
return true;
}
}
else slack[y] = min(slack[y],gap);
}
return false;
}
void KM_match(){
memset(match,255,sizeof(match));
for(int i = 1; i <= n; i++) LX[i] = *max_element(G[i]+1,G[i]+1+n);
memset(LY,0,sizeof(LY));
for(int i = 1; i <= n; i++){
memset(slack,INF,sizeof(slack));
while(true){
memset(visx,0,sizeof(visx));
memset(visy,0,sizeof(visy));
if(dfs(i)) break;
int d = INF;
for(int j = 1; j <= n; j++) if(!visy[j]) d = min(d,slack[j]);
for(int j = 1; j <= n; j++) if(visx[j]) LX[j]-=d;
for(int j = 1; j <= n ;j++) if(visy[j]) LY[j]+=d;
else slack[j]-=d;
}
}
for(int i = 1; i <= n; i++) printf("%d ",match[i]);
}
int main(){
scanf("%d",&n);
for(int i = 1; i <= n; i++) for(int j = 1; j <= n; j++){
scanf("%d",&G[i][j]);
G[i][j] = log(G[i][j])*1000000;
}
KM_match();
puts("");
return 0;
}
\(H.Hour\ for\ a\ Run\)
签到
//#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<bits/stdc++.h>
using namespace std;
function<void(void)> ____ = [](){ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0);};
int n,m;
int main(){
____();
cin >> n >> m;
for(int i = 1; i < 10; i++) cout << int(ceil((n*m*i)/10.0)) << ' '; cout << endl;
return 0;
}
\(I.Interplanetary\)
离线之后按顺序加点跑floyd
//#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<bits/stdc++.h>
using namespace std;
function<void(void)> ____ = [](){ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0);};
const int MAXN = 1e5+7;
const int INF = 0x3f3f3f3f;
struct Query{
int u,v,k,id;
Query(){}
Query(int u, int v, int k, int id){
this->u = u;
this->v = v;
this->k = k;
this->id = id;
}
}Q[2][MAXN];
int n,m,qs,res[MAXN],temp[MAXN],initG[444][444],q[2],G[444][444];
void solve(){
vector<int> tmp(n),nodes(n);
for(int i = 0; i < n; i++){
tmp[i]=temp[i+1];
nodes[i]=i+1;
}
sort(tmp.begin(),tmp.end());
tmp.erase(unique(tmp.begin(),tmp.end()),tmp.end());
function<bool(int,int)> cmp[2] = {
[](int x, int y){ return temp[x] < temp[y]; },
[](int x, int y){ return temp[x] > temp[y]; }
};
for(int op = 0; op <= 1; op++){
for(int i = 1; i <= n; i++) for(int j = 1; j <= n; j++) G[i][j] = initG[i][j];
sort(nodes.begin(),nodes.end(),cmp[op]);
if(!op) sort(tmp.begin(),tmp.end(),less<int>());
else sort(tmp.begin(),tmp.end(),greater<int>());
sort(Q[op]+1,Q[op]+1+q[op],[](const Query &x, const Query &y){ return x.k < y.k; });
for(int i = 1, cur = 0; i <= q[op]; i++){
while(cur<n){
if((!op&&temp[nodes[cur]]>tmp[Q[op][i].k-1])||(op&&temp[nodes[cur]]<tmp[Q[op][i].k-1])) break;
int node = nodes[cur++];
for(int u = 1; u <= n; u++) for(int v = 1; v <= n; v++)
G[u][v] = G[v][u] = min(G[u][v],G[u][node]+G[node][v]);
}
int u = Q[op][i].u, v = Q[op][i].v, ID = Q[op][i].id;
res[ID] = G[u][v]==INF?-1:G[u][v];
}
}
}
int main(){
scanf("%d %d",&n,&m);
for(int i = 1; i <= n; i++) scanf("%d",&temp[i]);
memset(initG,INF,sizeof(initG));
for(int i = 1; i <= n; i++) initG[i][i] = 0;
for(int i = 1; i <= m; i++){
int u, v, d;
scanf("%d %d %d",&u,&v,&d);
initG[u][v] = initG[v][u] = d;
}
scanf("%d",&qs);
for(int i = 1; i <= qs; i++){
int u, v, k, op;
scanf("%d %d %d %d",&u,&v,&k,&op);
Q[op][++q[op]] = Query(u,v,k,i);
}
solve();
for(int i = 1; i <= qs; i++) printf("%d\n",res[i]);
return 0;
}
\(J.Jar\ of\ Water\ Game\)
按题意模拟即可
//#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<bits/stdc++.h>
using namespace std;
function<void(void)> ____ = [](){ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0);};
int n,m;
int dec(char ch){
if(ch=='A') return 1;
else if(ch=='D') return 10;
else if(ch=='Q') return 11;
else if(ch=='J') return 12;
else if(ch=='K') return 13;
else return ch-'0';
}
struct P{
bool wildcard,tag;
vector<int> card;
int get(){
if(wildcard){
if(tag) tag = false;
else{
wildcard = false;
return -1;
}
}
map<int,int> cards;
for(int c : card) cards[c]++;
int minn = 6;
for(auto p : cards) minn = min(minn,p.second);
for(auto p : cards){
if(p.second!=minn) continue;
card.erase(find(card.begin(),card.end(),p.first));
return p.first;
}
}
void insert(int c){
if(c==-1) wildcard = tag = true;
else card.emplace_back(c);
}
}player[20];
bool check(int ID){
if(player[ID].wildcard) return false;
if(player[ID].card[0]!=player[ID].card[1]) return false;
if(player[ID].card[1]!=player[ID].card[2]) return false;
if(player[ID].card[2]!=player[ID].card[3]) return false;
return true;
}
int main(){
scanf("%d %d",&n,&m);
for(int i = 1; i <= n; i++){
char cd[10];
scanf("%s",cd);
player[i].card.resize(4);
for(int k = 0; k < 4; k++) player[i].card[k] = dec(cd[k]);
if(i==m) player[i].wildcard = player[i].tag = true;
else player[i].wildcard = player[i].tag = false;
}
for(int i = 1; i <= n; i++) if(check(i)) return printf("%d\n",i),0;
int now = m;
while(true){
int nxt = now+1==n+1?1:now+1;
player[nxt].insert(player[now].get());
if(check(now)) break;
now = nxt;
}
printf("%d\n",now);
return 0;
}
\(K.Keep\ Calm\ and\ Sell\ Balloons\)
矩阵快速幂,要找出递推公式
首先我们令\(f[n]\)表示\(2·n\)的矩阵从一个角开始走回到它垂直位置的方案数,可以发现\(f[n]=2·f[n-1], f[1]=1\),即\(f[n]=2^{n-1}\)
现在我们定义\(g[n]\)为从矩阵的一个角开始走走完整个矩阵的方案数,模拟一下方案数可以找到递推式:\(g[n]=f[n]+2·g[n-1]+4·g[n-2]\)
即\(g[n]\ =\ 2·g[n-1]+4·g[n-2]+2^{n-1},g[0]=0,g[1]=1\)
\(f[n]\)容易得出,\(2·g[n-1]\)的情况在第一张图,\(4·g[n-2]\)的情况在第二张图
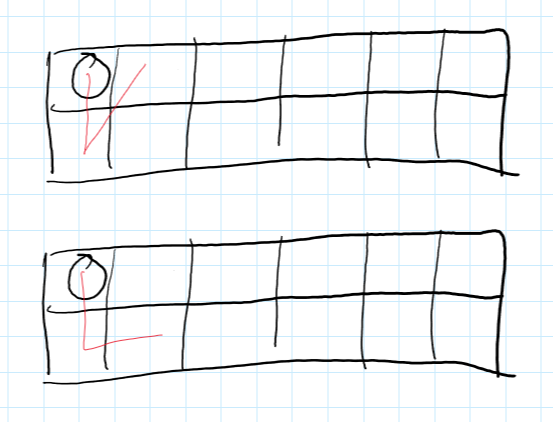
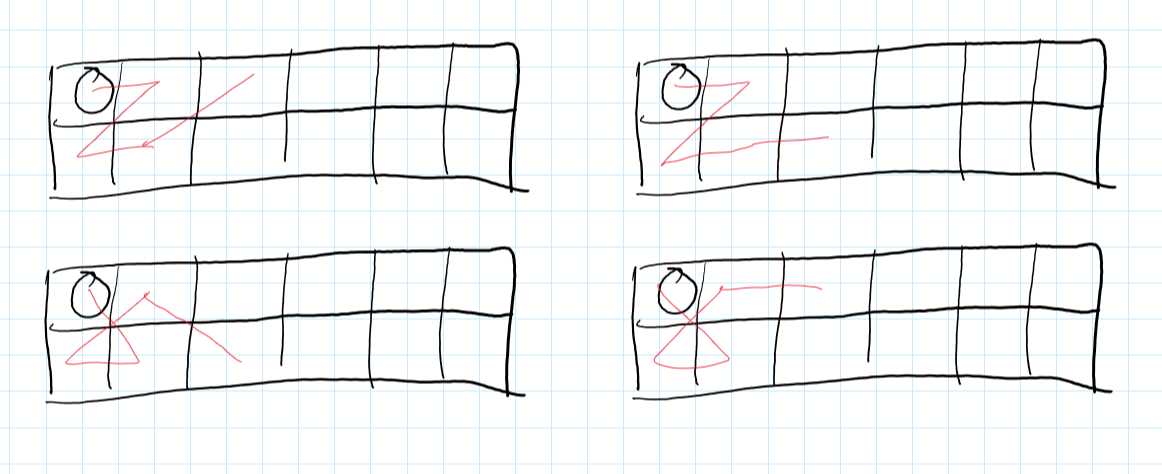
接下来我们定义\(h[n]\)为从矩阵的中间出发走完整个矩阵的方案数,可以把从中间出发走完整个矩阵分成两部分:
- 先从一边走回到垂直位置
- 再走完另一边
可以得到如下递推式:
其中第一个\(2\)是因为有上下两块,第二个\(2\)是因为可以先向右回到垂直位置再走完左边,也可以先向左回到垂直位置再走完右边,方案是对称的
然后找一下\(h[n]\)和\(h[n-1]\)的关系
所以最后答案就是\(h[n]+4·g[n]\)
!注意啊要从\(2\)开始递推,\(g[2] \ne 2·g[1]+4·g[0]+f[2]\)
//#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<bits/stdc++.h>
using namespace std;
function<void(void)> ____ = [](){ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0);};
using LL = int_fast64_t;
const LL MOD = 1e9+7;
struct Matrix{
LL m[6][6];
Matrix(int init = 1){
for(int i = 1; i <= 5; i++) for(int j = 1; j <= 5; j++){
if(i!=j) m[i][j] = 0;
else m[i][j] = init;
}
}
Matrix operator*(const Matrix rhs){
Matrix res(0);
for(int i = 1; i <= 5; i++){
for(int j = 1; j <= 5; j++){
for(int k = 1; k <= 5; k++)
res.m[i][j] = (res.m[i][j]+m[i][k]*rhs.m[k][j])%MOD;
}
}
return res;
}
Matrix operator*=(const Matrix rhs){
return *this = (*this)*rhs;
}
};
Matrix qpow(Matrix A, LL b){
Matrix res(1);
while(b){
if(b&1) res*=A;
b >>= 1;
A*=A;
}
return res;
}
LL n;
int main(){
scanf("%I64d",&n);
if(n==1) return puts("2"),0;
Matrix mat(0);
mat.m[1][1] = 2;
mat.m[1][3] = 16;
mat.m[2][2] = 2;
mat.m[2][3] = 4;
mat.m[2][4] = 2;
mat.m[3][2] = 1;
mat.m[4][4] = 2;
mat.m[5][5] = 1;
mat = qpow(mat,n-2);
printf("%I64d\n",(6*mat.m[1][2]+mat.m[1][3]+2*mat.m[1][4]+mat.m[1][5]+4*(6*mat.m[2][2]+mat.m[2][3]+2*mat.m[2][4]+mat.m[2][5]))%MOD);
return 0;
}
\(L.Less\ Coin\ Tosses\)
答案就是\(C(n,0)%2+C(n,1)%2+...+C(n,n-1)%2+C(n,n-1)%2\)
根据卢卡斯定理,答案就是2的\(N\)二进制位中1的个数次幂
//#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<bits/stdc++.h>
using namespace std;
function<void(void)> ____ = [](){ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0);};
int_fast64_t n;
#define lowbit(x) ((x)&(-x))
int main(){
scanf("%I64d",&n);
int_fast64_t res = 1;
while(n) res <<= 1,n-=lowbit(n);
printf("%I64d\n",res);
return 0;
}
\(M.Maratona\ Brasileira\ de\ Popcorn\)
二分答案判定即可
//#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<bits/stdc++.h>
using namespace std;
function<void(void)> ____ = [](){ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0);};
const int MAXN = 1e5+7;
using LL = int_fast64_t;
int n,c,t,A[MAXN];
bool check(int mid){
int cur = 0, tot = 1;
for(int i = 1; i <= n; i++){
if(mid*1ll*t<A[i]) return false;
if(mid*1ll*t>=cur+A[i]) cur+=A[i];
else{
tot++;
cur = A[i];
}
}
return tot<=c;
}
int solve(){
int l = 1, r = 1e9+7;
while(l<=r){
int mid = (l+r) >> 1;
if(check(mid)) r = mid - 1;
else l = mid + 1;
}
return l;
}
int main(){
scanf("%d %d %d",&n,&c,&t);
for(int i = 1; i <= n; i++) scanf("%d",&A[i]);
printf("%d\n",solve());
return 0;
}

