树的存储结构
三种表示方法
- 双亲表示法
- 孩子表示法
- 孩子兄弟表示法
一、双亲表示法
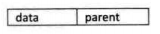
data:数据域,存储结点的数据信息
parent:指针域,存储结点的双亲在数组中的下标
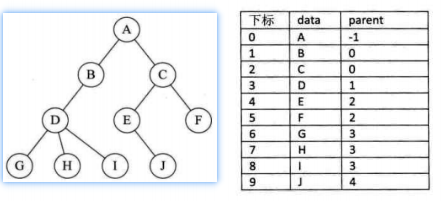
查找结点的双亲的时间复杂度:O(1)
查找结点的孩子的时间复杂度:需要遍历整个结构 //因为需要遍历所有结点的双亲,找到双亲相同的所有结点
改进:增加长子域(firstchild)
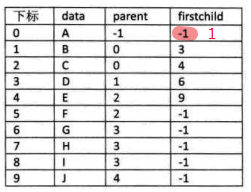
对于只有0个或者1个孩子的结点,这样的结构就可以找到结点的孩子了;
对于2个孩子的结点,这样的结构知道了长子是谁,另一个当然就是次子了
另外,可以增加一个右兄弟域来体现兄弟关系
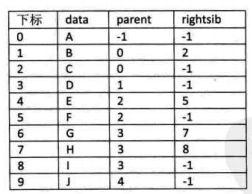
每一个结点,如果右兄弟存在,就记录右兄弟的坐标,如果右兄弟不存在,就赋值为-1
二、孩子表示法
多重链表表示法:每个结点有多个指针域,其中每个指针指向一棵子树的根节点。
由于每个结点的度,也就是它的孩子个数是不同的,所以这里有两种方案来解决。
- 方案一:每个结点指针域的个数等于树的度

data :数据域
child1~childd:指针域,指向该结点的各个孩子的结点
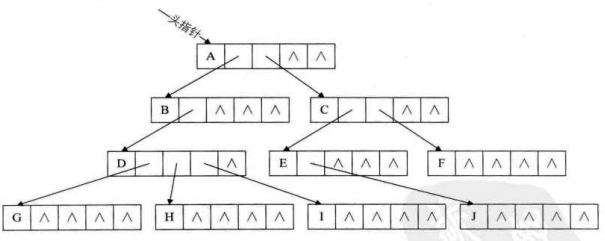
缺点:这种方法对于树中各节点的度相差很大时,显然是很浪费空间的,因为有很多的结点它的指针域是空的。
改进:既然很多指针域可能为空,那么可以按需分配空间
- 方案二:每个结点指针域的个数等于该结点的度,再专门取一个位置来存储结点指针的个数

data :数据域
degree :度域,也就是存储该结点的孩子结点的个数
child1~childd:指针域,指向该结点的各个孩子的结点
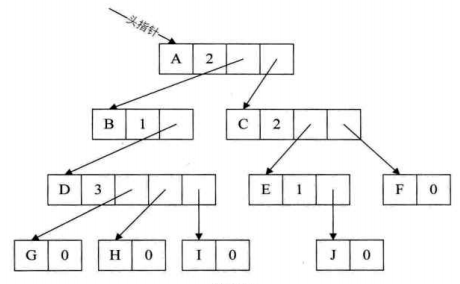
优点:克服了浪费空间的缺点,对于空间利用率是提高了。
缺点:由于各个结点的链表是不同的结构,加上要维护结点的度的数值,在运算上就会带来时间上的损耗。
改进:既减少空指针的浪费,又能使结点结构相同
- 方案二改进版,就是孩子表示法
把每个结点的孩子结点排列起来,以单链表作存储结构,则n个结点有n个孩子链表,如果是叶子结点则此单链表为空。
然后,n个头指针又组成一个线性表,采用顺序存储结构,存放进一个一维数组中。






