机器学习中常见优化方法汇总
机器学习中数学优化专门用于解决寻找一个函数的最小值的问题。这里的函数被称为cost function或者objective function,或者energy:损失函数或者目标函数。
更进一步,在机器学习优化中,我们并不依赖于被优化的函数的数学解析表达式,我们通过使用$scipy.optimize$从而实现类似黑盒优化。
了解你的优化问题本身
并不是所有的优化问题都是一样的,如果你能对你待优化的问题本身有一个深刻的理解,这样可以选择正确的优化方法。
1.其中非常重要的一点就是要考察问题本身的维数。问题本身数据的维数(标量变量的个数)决定了优化问题的规模。
2.convex和non-convex优化
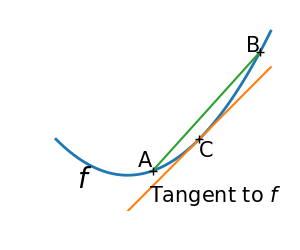
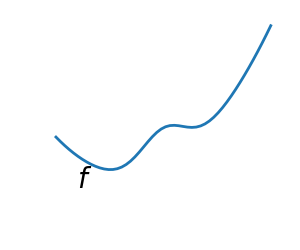
凸函数的特征:
- $f$总是在其切线之上
- 或者说,对于两个点$A,B$,如果$A<C<B$,则$f(C)$总是在线段$f(A),f(B)$之间
凸函数优化相对非常简单。
3.函数光滑与否(是否处处可导)
4. loss函数以及gradient函数是否存在噪声
如果gradient没有解析式,那么我们都须通过计算式计算,这必然导致误差。
5. 是否有限制条件
比如,下图中就要求优化只能在$x_1,x_2 \in (-1,1)$间优化

常见的优化方法
Brent’s method
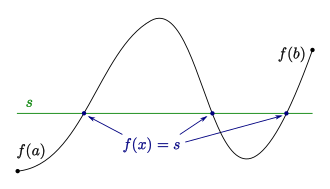
理论依据是中值定理,对于一个连续函数,$f$,如果两个端点a,b的函数值$f(a)f(b)<0$,则$(a,b)$之间必然存在一个驻点(导数为0),我们可以不断迭代最终求得驻点;
from scipy import optimize def f(x): return -np.exp(-(x - 0.7)**2) result = optimize.minimize_scalar(f) result.success # check if solver was successful x_min = result.x
gradient based methods
简单梯度下降法
原理如教科书的描述,根据梯度下降的方向去做数值变更和迭代,最终求得驻点。
存在的问题是:参数调整时可能反复跨过驻点从而形成震荡,虽然减少参数调整的布幅可以减轻这个问题,但是无法彻底解决。
共轭梯度下降
共轭算法在简单梯度下降基础上增加一个摩擦项(friction term),每个step依赖于梯度最近的两个值,这样可以有效解决反复震荡问题。
def f(x): # The rosenbrock function return .5*(1 - x[0])**2 + (x[1] - x[0]**2)**2 optimize.minimize(f, [2, -1], method="CG")
梯度优化方法需要loss函数的雅可比(梯度)值,虽然即使你不传入导数(雅可比矩阵是针对y值为向量的情况下的梯度向量),算法也能够通过数值计算方法算出来,但是如果有解析表达式,我们传入这个值会大大提升收敛效率.
def jacobian(x): return np.array((-2*.5*(1 - x[0]) - 4*x[0]*(x[1] - x[0]**2), 2*(x[1] - x[0]**2))) optimize.minimize(f, [2, 1], method="CG", jac=jacobian)
注意:通过传入解析表达式后,只需要28次就能收敛,而之前需要108次迭代才能收敛。
牛顿梯度法(Newton and quasi-newton methods)
def f(x): # The rosenbrock function return .5*(1 - x[0])**2 + (x[1] - x[0]**2)**2 def jacobian(x): return np.array((-2*.5*(1 - x[0]) - 4*x[0]*(x[1] - x[0]**2), 2*(x[1] - x[0]**2))) optimize.minimize(f, [2,-1], method="Newton-CG", jac=jacobian)
BFGS
BFGS在牛顿法基础上细调了Hessian矩阵的估算方法
L-BFGS
L-BFGS位于BFGS和共轭梯度法之间。对于非常高维(大于250个)的loss函数,Hessian矩阵的计算是非常耗时的,L-BFGS keeps a low-rank version.
非梯度优化方法
Powell算法
Nelder-Mead
带约束条件的函数优化
盒子边界
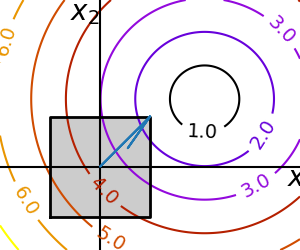
def f(x): return np.sqrt((x[0] - 3)**2 + (x[1] - 2)**2) optimize.minimize(f, np.array([0, 0]), bounds=((-1.5, 1.5), (-1.5, 1.5)))
通用约束:拉格朗日乘数法化约束为对偶无约束的优化问题
def f(x): return np.sqrt((x[0] - 3)**2 + (x[1] - 2)**2) def constraint(x): return np.atleast_1d(1.5 - np.sum(np.abs(x))) x0 = np.array([0, 0]) optimize.minimize(f, x0, constraints={"fun": constraint, "type": "ineq"})

