机器学习数学知识积累之高等数学微积分
正余弦等三角函数定义及基本性质回顾
定义:

运算性质:

泰勒展开式
泰勒公式是将一个在x=x0处具有n阶导数的函数f(x)利用关于(x-x0)的n次多项式来逼近函数的方法。
$$f(x) = \frac{f(x_0)}{0!} + \frac{f^{'}(x_0)}{1!}(x-x_0) + \frac{f^{''}(x_0)}{2!}(x-x_0)^{2} + \frac{f^{'''}(x_0)}{3!}(x-x_0)^{3}+... + \frac{f^{n}(x_0)}{n!}(x-x_0)^{n}+R_n(x)$$
其中$R_n(x)$是$(x-x_0)^{n}$的高阶无穷小
通常,我们在x0 = 0 处展开,将$f(x_0),f^{'}(x_0),...,f^{n}(x_0)$的值带入泰勒展开式就得到
$$f(x) = \frac{f(0)}{0!} + \frac{f^{'}(0)}{1!}x + \frac{f^{''}(0)}{2!}x^{2} + \frac{f^{'''}(0)}{3!}x^{3}+... + \frac{f^{n}(0)}{n!}x^{n}+R_n(x)$$
在实际科学计算中,我们通过二阶泰勒展开,就可以对$f(x)$实现近似计算
常用函数的泰勒展开
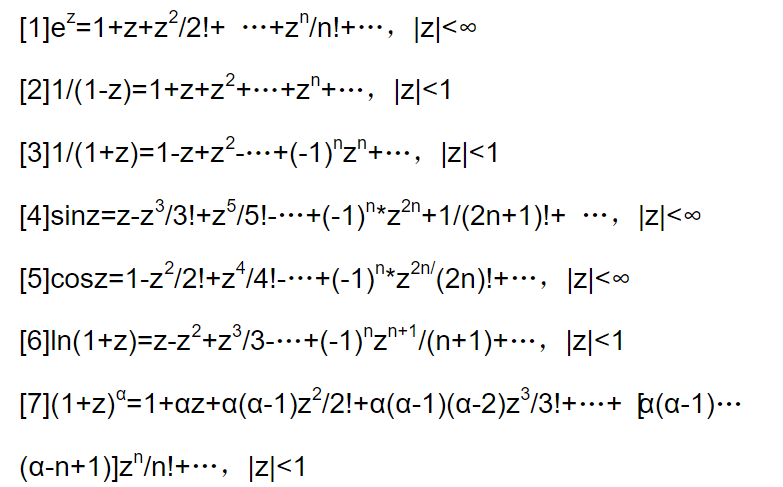
拉格朗日乘数法优化有约束条件的函数
我们知道机器学习本质上是给定一组数据集后对损失函数进行优化求解。优化的方法最常见的是随机梯度下降法,而神经网络中的优化更进一步使用后向传播的梯度下降方法。但是对于有约束条件的函数优化问题,直接使用梯度下降是有困难的。这时,拉格朗日乘数法就能有效实现这类问题的优化。
https://blog.csdn.net/WuSnake123/article/details/58635726
拉格朗日优化基本思想
作为一种优化算法,拉格朗日乘子法主要用于解决约束优化问题,它的基本思想就是通过引入拉格朗日乘子来将含有n个变量和k个约束条件的约束优化问题转化为含有(n+k)个变量的无约束优化问题。拉格朗日乘子背后的数学意义是其为约束方程梯度线性组合中每个向量的系数。
如何将一个含有n个变量和k个约束条件的约束优化问题转化为含有(n+k)个变量的无约束优化问题?拉格朗日乘数法从数学意义入手,通过引入拉格朗日乘子建立极值条件,对n个变量分别求偏导对应了n个方程,然后加上k个约束条件(对应k个拉格朗日乘子)一起构成包含了(n+k)变量的(n+k)个方程的方程组问题,这样就能根据求方程组的方法对其进行求解。
解决的问题模型为约束优化问题:
min/max a function f(x,y,z), where x,y,z are not independent and g(x,y,z)=0.
即:min/max f(x,y,z)
s.t: g(x,y,z)=0
数学实例
求双曲线xy=3上离远点最近的点。
我们先根据上述问题描述提炼出问题对应的数学模型,即:
$min f(x,y) = x^2+y^2 \: s.t.: xy=3 $
这是一个典型的约束优化问题,其实最简单的方法是将变量进行替换,随后使用传统的求导取0来优化。但是我们还是通过使用拉格朗日乘数法的思想来求解用于理解拉格朗日乘数法的核心。
我们将$x^2+y^2=c$的曲线族画出来,当曲线族中的圆与双曲线$xy=3$相切时,切点到原点的距离是最短的。也就是说当f(x,y)=c的等高线与双曲线相切时,我们可以得到上述优化问题的极值。
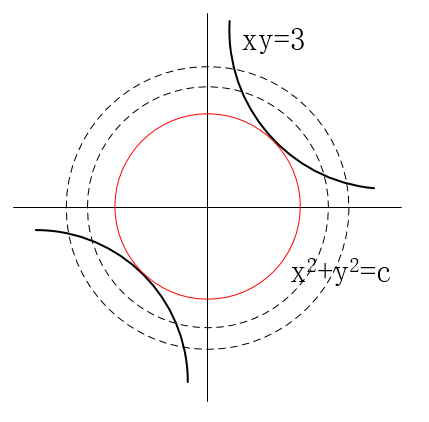
现在原来的优化问题就可以等价为:求当f(x,y)和g(x,y)相切时,x,y的值是多少?
如果两个曲线相切,那么他们的切线在切点必然相同,即法向量是相互平行的.$\triangledown f // \triangledown g $,也就是说存在一个标量$\lambda$使得 $\triangledown f = \lambda * \triangledown g $。这时,我们就将原来的约束优化问题转化为了一种对偶等价的无约束的优化问题,如下:
$f_x'=\lambda*g_x';f_y'=\lambda*g_y';xy=3$
通过求解以下方程组:
$$\left\{\begin{matrix}2x = \lambda*y\\ 2y = \lambda*x\\ xy = 3\end{matrix}\right.$$
求得:$\lambda=2;\lambda=-2$,当$\lambda=2$时,$(x,y)=(\sqrt3,\sqrt3)$,当$\lambda=-2$时,无解。
通过这个例子,我们就可以体会到拉格朗日乘数法通过引入拉格朗日乘子($\lambda$)将原来的约束优化问题转换为无约束的方程组问题。
拉格朗日乘数法的基本形态:
求函数 在满足
在满足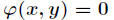 下的条件极值,可以转化为函数
下的条件极值,可以转化为函数 的无条件极值问题。
的无条件极值问题。
当取得最优解时
▽[f(x,y)+λ(g(x,y)−1)]=0, λ≠0
一旦通过上述方程求出$\lambda$的值,便容易求出无约束极值和极值对应的点:
F(x,y)=f(x,y)+λ(g(x,y)−c)
新方程F(x,y)在达到极值时与f(x,y)相等,因为F(x,y)达到极值时g(x,y)−c总等于零。
上述式子取得极小值时其导数为0,即▽f(x)+▽∑λigi(x)=0,也就是说f(x)和g(x)的梯度共线
例题:
给定椭球

求这个椭球的内接长方体的最大体积。这个问题实际上就是条件极值问题,即在条件
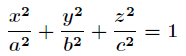
下,求 的最大值。
的最大值。
当然这个问题实际可以先根据条件消去 ,然后带入转化为无条件极值问题来处理。但是有时候这样做很困难,甚至是做不到的,这时候就需要用拉格朗日乘数法了。通过拉格朗日乘数法将问题转化为
,然后带入转化为无条件极值问题来处理。但是有时候这样做很困难,甚至是做不到的,这时候就需要用拉格朗日乘数法了。通过拉格朗日乘数法将问题转化为

对 求偏导得到
求偏导得到

联立前面三个方程得到 和
和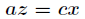 ,带入第四个方程解之
,带入第四个方程解之

带入解得最大体积为

拉格朗日乘数法对一般多元函数在多个附加条件下的条件极值问题也适用。
积分的降幂分布积分法
$\int_{a}^{b}udv = \left [ uv \right ]^b_a-\int_{a}^{b}vdu$



