机器学习数学知识积累之概率论
排列组合遵循的加法原理和乘法原理
加法原理
设完成一件事有m种方式，第一种方式有$n_1$种方法，第二种方式有$n_2$种方法，...，第m种方式有$n_m$种方法，
则完成这件事儿，一共就有$n_1+n_2+n_3+..+n_m$种方法
乘法原理
设完成一件事儿有$ r $个步骤，第一个步骤有$ n_1 $ 种方法，第二个步骤有$ n_2 $ 种方法，第三个步骤有$ n_3 $ 种方法，...第n个步骤有$ n_r $ 种方法，
则完成这件事儿一共就有 $ n_1 \times n_2 \times n_3 \times ... \times n_r $种方法
排列与组合
排列的定义
从n个不同元素中，任取m(m≤n,m与n均为自然数,下同）个元素按照一定的顺序排成一列，叫做从n个不同元素中取出m个元素的一个排列；从n个不同元素中取出m(m≤n）个元素的所有排列的个数，叫做从n个不同元素中取出m个元素的排列数，用符号 A(n,m）表示。
组合的定义
从n个不同元素中，任取m(m≤n）个元素并成一组，叫做从n个不同元素中取出m个元素的一个组合；从n个不同元素中取出m(m≤n）个元素的所有组合的个数，叫做从n个不同元素中取出m个元素的组合数。用符号 C(n,m) 表示。
如何判断是排列还是组合问题？排列和组合的共同点是从n个不同元素中取出m个元素，不同点是是否和顺序有关，和顺序有关就是排列问题，和顺序无关就是组合问题。一般地组合数等于排列数除以次序
样本空间
实验的所有基本结果的集合被称为样本空间，一般记为$S$,样本空间中的每一个实验结果被称为样本点，每一个基本的实验结果单个构成的事件被称为基本事件，基本事件必然两两互斥。样本点的数目可以是有限的，也可能是无限的？？？
样本空间抽象示例(二维随机变量联合分布)
事件(集合)的计算性质
由于概率论中的事件实际上就是样本空间中样本值(结果)的集合，很多概率计算也会应用到集合的性质，下面罗列出来常用的计算性质,其中对偶律对于多个集合都是满足的。
事件往往用语言来描述，但是我们需要具有将语言描述映射为集合的抽象能力。比如$E=投骰子出现偶数$的事件等价于$E=\{ 2,4,6 \}$
事件空间是由样本空间中的值(结果)任意组合形成的所有集合集,比如执公平骰子的点数形成的样本空间为｛1｝,｛2｝,｛3｝,｛4｝,｛5｝,｛6｝。那么一个事件:$E(骰子的结果是偶数)={2,4,6}$，这里的骰子数值任意组合可以形成相应的事件空间,比如$E(骰子的结果<3)={1,2}，E(骰子的结果不大于5)={1,2，3，4}$等。。
$\overline{ABC} = \bar A \bigcup \bar B \bigcup \bar C$
$\overline{A \bigcup B \bigcup C} = \bar A \bar B \bar C$
概率
概率反映了人们对某些事件的了解程度。以下几个原因导致为什么会产生概率这个学科：
1. 人们对这个世界的无知。由于世界太复杂，人类并不能很好的把握事件发生的因果关系，这时就只能通过观察来发现事件发生的机会，比如新生儿是男孩还是女孩，暑假天气超过35度的会是哪些天。。。像这类问题，人们可能对影响结果的因素并无准确把握，因此只能通过观察来总结事件发生的规律来认识世界；
2. 某些事件本身就具有随机性，即使"相同"的测试条件，结果却具有不确定性，不可预测性，比如我们抽奖时具体会抽到哪一张票这个也是完全随机的，受票箱中票的分布，抽奖人当时的心情，抽的地点等多重影响，这就表现出其随机的特性。再比如执骰子，本身出来的是1，2，3，4，5，6哪一个点本身就是随机的，结果受我们出力大小，投掷方向，地面光滑，空气湿度等等因素所影响，在投骰子之前我们无法预知结果。
3.即便有时对于某些事件发生的规律有了本质了解，但是联合起来研究非常复杂，我们可能倾向于结合起来当作随机现象去研究。比如研究热运动的现象，虽然每个分子热运动的规律有成熟的理论模型，但是我们往往关心的是物质(巨量分子)的热运动规律，而不是单个分子的情况，理论上虽然可以通过建立每个分子的热运动方程去研究，但是数量太过巨大，每个分子的运动又具有独立性，这时我们可能希望从宏观层面通过随机现象来研究。
正因为这两个原因，我们使用统计学的方法去了解这类随机现象具有的统计特征，从而从概率上来把握这些现象
在个别实验中结果的出现具有不确定性，但在大量重复试验中又呈现规律性的非确定性现象称为随机现象
大量同类随机现象所呈现的固有规律(不以人们的主观意志而改变)为随机现象的统计规律性
概率论与数理统计就是研究揭示随机现象的统计规律性的数学学科。
概率定义的演变
频率学派:概率表征为大量实验观察后得到的事件发生的频率
贝叶斯学派:概率为根据以往的资料或者经验，形成的关于随机事件发生可能性的主观印象--是一个先验信息，比如:考察某地区男婴的出身概率;考察某人是某案件嫌疑人的概率
如果既没有办法做大量随机实验，又没有任何主观印象，这时也就是说我们对待研究的现象是无信息的，这种情况下贝叶斯假设基本事件发生是没有任何偏好的，都是等可能的。
概率的公理化定义:
频率学派和贝叶斯学派都是有道理的，但是没有将概率提升到数学理论的高度，前苏联科学家柯尔莫哥洛夫做了更进一步的抽象：
概率为一个函数
非负性： $1>P>0$
规范性：$P(S)=1$
可加性： $P(A+B+C) = P(A)+P(B)+P(C)， A,B,C两两互斥$
概率和频率
频率是n次实验中事件发生的次数除以总的实验次数，频率是一个随机变量，其值随着实验次数不同而不同。
概率是随机事件发生可能性大小的客观度量！！概率具有客观性和唯一性
依据大数定律，当实验次数趋于无穷大时，频率趋近于概率
随机试验
为了研究随机现象的统计规律性，需要对随机现象进行观察和实验。随机实验具有以下特点：
1. 可以在 " 相同 " 条件下重复进行: 可重复性
2.可以弄清实验的全部结果： 结果可知性
3. 实验前不能预言将出现哪个结果： 不可预言性
随机事件，样本空间
随机实验中可能发生也可能不发生的事情称为随机事件。比如，执硬币观察正反面出现的情况这个实验，"出现正面"和出现反面这两种结果都可以看成随机事件。需要注意的是如果出现与实验目的无关的情况，也不能称之为事件。比如抛硬币时骰子可能既没不是正面也不是反面而是树立起来不倒，这个结果不是我们关心的结果，因此不作为事件。
$A=\{出现正面\}, B=\{出现反面\}$
再例如：$E3$:记录某电话总台一天接到的呼叫次数这个实验中，以下都为事件:
$A =\{呼叫次数为偶数\} $ 复合事件：由若干基本事件组合而成的事件,是样本空间的子集
$B =\{呼叫次数为奇数\} $
$C =\{呼叫次数大于3\} $
$A_i =\{呼叫次数为i\} , i = 0,1,2,3,4.. $ 基本事件:必然发生一个并且仅发生一个的最简单互斥事件，为单点集，$A_0,A_1,A_2,A_3,..A_i$
$\Omega =\{呼叫次数为0或者正整数\} $ 必然事件对应着样本空间这个全集
样本空间是所有基本事件组成的集合，通过将事件和集合做了一一对应，我们就可以使用集合论的知识方便对随机现象进行数学研究。
概率的度量
概率大于0并且小于1，其值可以和幸运大转盘上面的画出的周长长度来度量
等可能概型:只要假设基本事件发生的机会均等，我们就称为等可能概型，分为:古典概型(有限个样本点:离散变量)和几何概型(无限个样本点：连续变量)
古典概率的性质
1. $0\leqslant P(A) \leqslant 1$
2. P(S) = 1
3. 若事件A,B互斥，则
$P(A+B) = P(A)+P(B)$
4. $P(\bar{A}) = 1-P(A)$
5. $P(\varnothing)=0$
6. $若 A\subset B ,则 P(A)\leqslant P(B)并且 P(B-A)=P(B)-P(A)$
7. $P(A-B) = P(A) - P(AB)$
古典概率的算法
$$P(A) = \frac{k}{n} = \frac{A中包含的基本事件数}{S中基本事件总数}$$
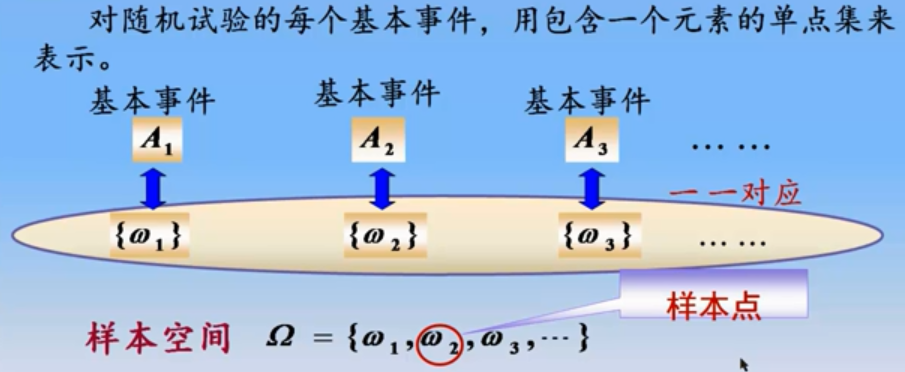
条件概率$P(A|B)$
上面我们提到概率反映了人们对某些事件的了解程度。比如对于同一个选择题，如果让一个完全不懂行的学渣来做，那么其由于完全不懂，正解是A的概率就是0.25。但是对于一个学霸来说，他可能已经完全可以排除其中的C,D项，但是对于A,B两项却拿不准，那么对该学霸来说，正解是A的概率就等于0.5了。从这里也可以看出当得知某些事情发生之后，我们对事情的了解也可能会发生改变。
这也可以引入下面的条件概率
$P(A|B) = P(AB)/P(B)$ B发生的前提下A发生的概率为B这个样本空间中A的样本数比率
条件概率也可以理解成A在B中所占有的比例
条件概率样本空间降低直观理解
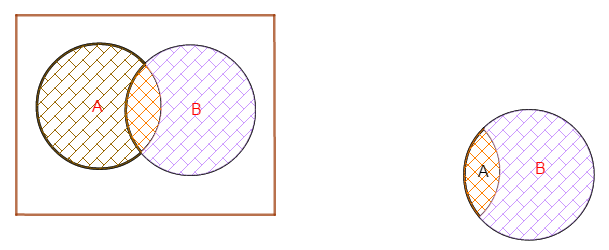
在古典条件概率$P(A|B)$的计算中，由于基本事件等概率，我们可以直接把条件事件B当作新的样本空间按照无条件概率的方式来计算，随后使用$E=AB$的样本点数除以新的样本空间样本总数。但是对于非古典概率，由于事件发生的可能性并不均等，故而不能用这个思路，而必须用条件概率定义来计算。
条件概率也满足概率的三条公理化定义，因此条件概率也具有古典概率的所有属性。就是$P(.|B)$可以认为是一种新的运算定义，满足：
$$P((A-B)|C) = P(A|C) - P(AB|C)$$
若$A_1,A_2,..A_n$互斥，则条件概率$P((A_1+A_2+...+A_n)|B) = P(A_1|B) + P(A_2|B) +...+ P(A_n|B) $
$$P(\bar{A}|B) = 1-P(A|B)$$
$$P(A_1-A_2|B) = P(A_1|B) - P(A_1A_2|B)$$
$$P(A_1\bigcup A_2|B) = P(A_1|B) + P(A_2|B) - P(A_1A_2|B)$$
乘法定理
$P(AB)=P(A)P(B|A)=P(B)P(A|B)$
全概率公式
$$P(B) = P(B\bigcap S) = P(B\bigcap \{A_1,A_2,..,A_n\}) = P(BA_1)+P(BA_2)+..+P(BA_n) = \sum P_{A_i}P_{B|A_i}$$
$ A_1,A_2,..A_n为S的一个划分，每个B总会伴随A_i发生而发生$
全概率可以理解为：先将导致B发生的所有条件都找全了，$A_1,A_2 ... A_n$， 然后将这些发生条件下的条件概率全部加起来就会得到B的总体概率，其中$A_1,A_2,...A_n$是所有能够导致B发生的事件集合，并且两两互斥。 这就是为什么叫做全概率的原因。
如下图所示，$ A_1,A_2,..A_6$是能够导致B发生的所有原因，B的概率就等于B在$ A_1,A_2,..A_6$条件下的条件概率的和集。全概率公式适合于事件还未发生，求解目标事件发生的概率预测，知因求果型问题的概率预测
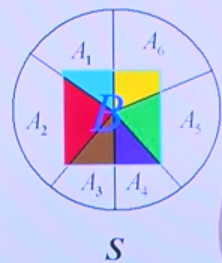
可以用下图更清楚地看出，使用一个$S$的有限划分，将样本空间分割，这些子空间和我们关注的事件交集比较好求解，注意本例是非古典概率计算(发生概率不均等)。其思想是化整为零
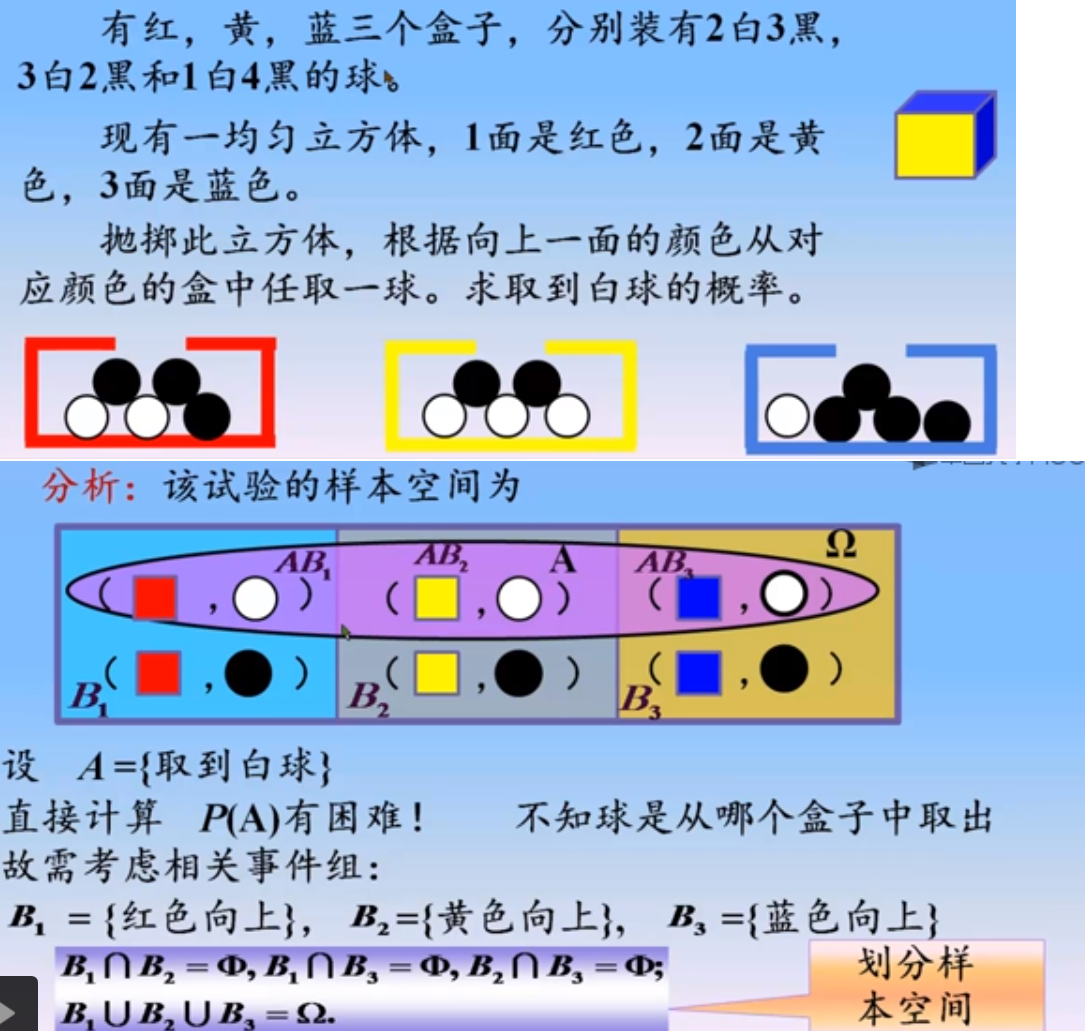
贝叶斯定理
$$P(A_i|B)=\frac{P(A_iB)}{P(B)} = \frac {P(A_i)P(B|A_i)}{\sum P(A_j)P(B|A_j)}$$
注意其数学含义可以理解为所有导致B发生的原因中$A_i$项所占的比例，
$P(A_i)$被称为验前概率，$P(A_i|B)$被称为验后概率。贝叶斯公式可以认为是使用$A_i$事件的验前概率来求解已知实际事件发生结果后的验后概率
贝叶斯定理解决的是已知结果，去找导致这个结果的原因的概率的问题。贝叶斯定理的两种应用：
1. 执果寻因型的原因事件概率计算
2. 基于新信息（事件已经发生）修正先验概率（计算后验概率）
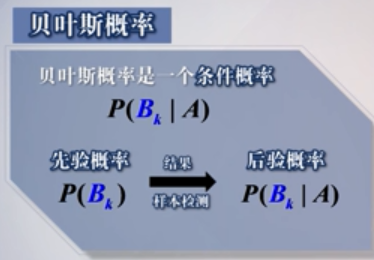
贝叶斯概率是一个条件概率，他的重要性是在于将先验概率和后验概率有机地结合起来。用实验获得的数据实现对原因$A_k$的重新认识。在实验之前，对$A_k$的认识$P(A_k)$为先验概率，
在实验之后，在$B$发生的条件下的$A_k$的条件概率$P(A_k|B)$为后验概率，后验概率的更新加深了对该原因$A_k$的认识。在随后，一般会使用这个新的后验概率作为新的先验概率使用，再次实验
会根据新的实验数据再次对这个先验概率做修正，形成新的先验概率。
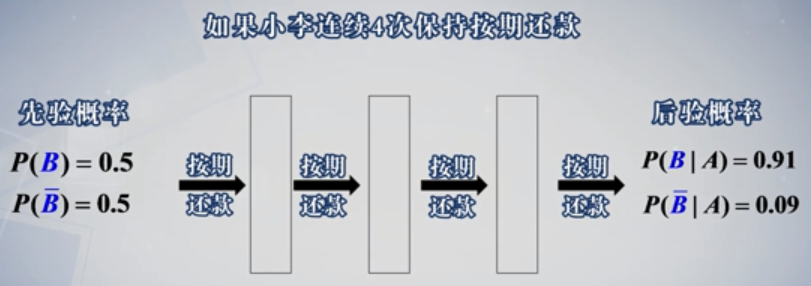
以银行信用评估模为例子，银行在对一个新的客户评估是否放贷时，由于对该客户无任何认识，会给他设定一个初始信用等级，后续通过还款记录不断更新对该客户的信用登记评估。
设 $B="小李守信", P(B)为小李守信的概率$，银行可能会给小李一个初始信用等级，假设$P(B)=P(\bar B) = 0.5 A="小李按期还款事件", P(A|B) = 0.9, P(A|\bar B) = 0.5$,
1. 根据以上假设，使用全概率公式计算初始按期还款的概率
$P(A)= P(B)P(A|B)+P(\bar B)P(A|\bar B)=0.7$
2.银行检测到小李第一次按时还款，也就是$A$事件发生了，该事件发生，银行从中对小你有什么新的后验认识呢？根据贝叶斯定理，我们来计算后验概率(在$A$发生的条件下，$B$事件的条件概率)
$P(B|A) = \frac{P(B)P(A|B)}{P(B)P(A|B)+P(\bar B)P(A|\bar B)}=0.64$
注意:银行从小李的一次按期还款事件就有充足的信心将小李守信等级从先验的守信概率0.5提高到后验的0.64！！
银行会使用新的后验概率作为后续信用评估模型中使用的先验概率，更新信用数据如下: $P(B) = P(B|A)= 0.64, P(\bar B) = 0.36$
3.这时如果小李再次提出贷款申请，银行将使用全概率公式重新计算其按期还款的概率
$P(A)= P(B)P(A|B)+P(\bar B)P(A|\bar B)=0.756$,这里也可以看到银行重新计算的还款概率也得到有效提升从0.7上升到0.756
4. 如果小李再次有按时还款的记录，银行进一步依据贝叶斯公式，重新计算其信用概率$P(B|A) = 0.76$,进一步提高。
后验概率密度:
$$f_{X\mid Y=y}(x) = {f_X(x) L_{X\mid Y=y}(x) \over {\int_{- \infty}^\infty f_X(x) L_{X\mid Y=y}(x)\,dx}}$$
注意:
LX | Y = y(x) = fY | X = x(y) 是似然函数
似然函数
似然函数是一种关于统计模型参数$\theta$, (比如$\theta$可能是概率$p$)的函数。给定输出x时，关于参数θ的似然函数L(θ|x)（在数值上）等于给定参数θ后变量X的概率：
$$L(\theta|x) = P(X=x|\theta)$$
概率（probability)和似然（likelihood)，都是指可能性，都可以被称为概率，但在统计应用中有所区别。概率是给定某一参数值，求某一结果的可能性的函数。似然函数往往用于给定了某一结果，去求解某一参数值的可能性。往往我们认为使得似然函数取得最大值的统计模型参数最为合理，最有说服力
例子:
考虑投掷一枚硬币的实验。通常来说，已知投出的硬币正面朝上和反面朝上的概率各自是pH = 0.5，便可以知道投掷若干次后出现各种结果的可能性。比如说，投两次都是正面朝上的概率是0.25。用条件概率表示，就是：
其中H表示正面朝上。
在统计学中，我们关心的是在已知一系列投掷的结果时，关于硬币投掷时正面朝上的可能性的信息。我们可以建立一个统计模型：假设硬币投出时会有pH 的概率正面朝上，而有1 − pH 的概率反面朝上。这时，条件概率可以改写成似然函数：
也就是说，对于取定的似然函数，在观测到两次投掷都是正面朝上时，pH = 0.5 的似然性是0.25（这并不表示当观测到两次正面朝上时pH = 0.5 的概率是0.25）。
如果考虑pH = 0.6，那么似然函数的值也会改变。
注意到似然函数的值变大了。这说明，如果参数pH 的取值变成0.6的话，结果观测到连续两次正面朝上的概率要比假设pH = 0.5时更大。也就是说，参数pH 取成0.6 要比取成0.5 更有说服力，更为“合理”。总之，似然函数的重要性不是它的具体取值，而是当参数变化时函数到底变小还是变大。对同一个似然函数，如果存在一个参数值，使得它的函数值达到最大的话，那么这个值就是最为“合理”的参数值。这就是最大似然估计的本质思想。
在这个例子中，似然函数实际上等于：
， 其中
。
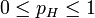如果取pH = 1，那么似然函数达到最大值1。也就是说，当连续观测到两次正面朝上时，假设硬币投掷时正面朝上的概率为1是最合理的。
类似地，如果观测到的是三次投掷硬币，头两次正面朝上，第三次反面朝上，那么似然函数将会是：
， 其中T表示反面朝上，。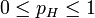
这时候，似然函数的最大值将会在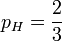
的时候取到。也就是说，当观测到三次投掷中前两次正面朝上而后一次反面朝上时，估计硬币投掷时正面朝上的概率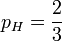是最合理的。
再比如，如果两次投掷取得的结果是$\{H,T\}$，则似然函数是:
$L(\theta | HT) = p(1-p)$,该函数取得极大值的点在0.5，也就是说硬币正反面等概率时最有可能出现$\{H,T\}$的实验结果,这和我们的直观相符。
概率论中的独立事件(independent)vs互斥（不相容）事件(disjoint)
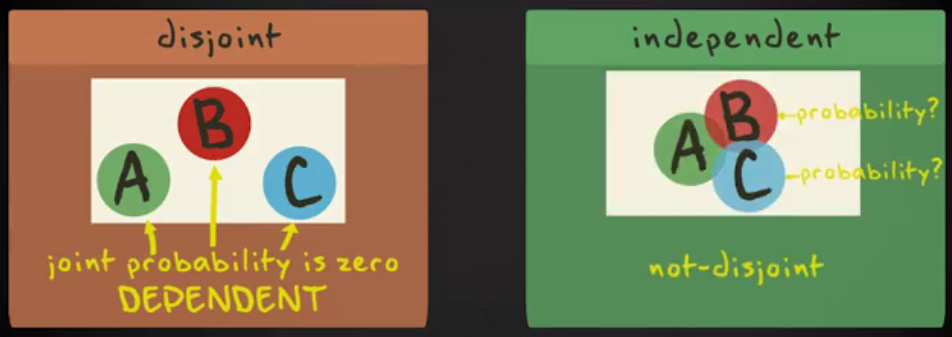
互斥事件/不相容事件（disjoint）
事件互不相容又叫互斥(disjoint),即两个事件不能同时发生.正是因为这一点实际上所有互斥事件都不是相互独立的（dependent），因为假设事件A发生，那么B必然不发生，反之亦然。或者说如果A发生，那么B发生的概率必然为0 $P(A|B) = 0$;也可以说A和B同时发生的概率为0， $P(AB)=0$
逆事件(对立事件,互补)(complemetary)
如果$A\bigcup B = S 并且A \bigcap B = 0$,则称$A和B$为逆事件，互补事件。也就是说互补事件必然是互斥事件，不可能同时发生。并且两个事件必然充满整个样本空间，两个互补事件概率之和为1
独立事件(independent)
事件相互独立指两个事件各自的发生与否与另一个事件的发生与否没有任何关系；比如：A与B独立,那么如果A发生,B可能发生也可能不发生，B是否发生以及发生的概率和A是否发生没有任何关系。
相互独立的事件可能是互斥的，也可能不互斥. $P(A∩B) = P(A)P(B)$ 是事件独立的充分必要条件. $P(A|B)=P(A)$
在现实生活中，事件之间相互独立并不是非常普遍的事情，很多时候由于我们未知的影响因子的存在会去影响着A发生后对B发生概率（只是我们并没有办法找出来或者解释清除是什么因素而已），而这或许就是我们机器学习需要去发现的规律所在
二项概率公式(n重伯努利实验A或者$\bar A$发生k次的概率)
$$P_n(k) = \binom{n}{k}p^k(1-p)^{n-k}$$
常见例子：掷骰子n次，出现k次6点的概率多少？连续射击目标50次，每次击中的概率0.08,那么至少命中两次的概率多少？这两个问题都可以看作n重伯努利实验，并使用上述公式
二项概率泊松逼近定理:
当$n\geq 10, p \leq 0.1$时可以使用以下公式，当$n\geq 10, p \geq 0.9$时可以使用逆事件
$$P_n(k) = \binom{n}{k}p^k(1-p)^{n-k} \approx \frac{\lambda ^k}{k!} e^{-\lambda} 其中 \lambda = np$$
什么是mosaic plot?
mosaic plot对于研究两个及两个以上categorical变量之间关系具有非常直观的优点:
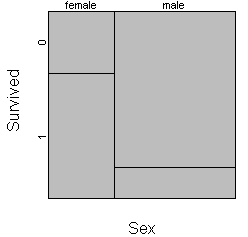
比如上面图中就可以明显看到titanic号上面大部分是男性，大约占63%， 而针对男女两类人分别考察其死亡率，可以看到男性死亡率远远高于女性，这一点实际上还原了当时撞山事故后的一个救生原则：妇女和儿童优先上救生船。
http://www.pmean.com/definitions/mosaic.htm
先验概率vs后验概率
http://blog.sina.com.cn/s/blog_4ce95d300100fwz3.html
验前概率（先验概率）就是通常说的概率，验后概率(后验概率)是一种条件概率，但条件概率不一定是验后概率。贝叶斯公式是由验前概率求验后概率的公式。
举一个简单的例子：一口袋里有3只红球、2只白球，采用不放回方式摸取，求：
⑴ 第一次摸到红球（记作A）的概率；验前概率
⑵ 第二次摸到红球（记作B）的概率；验前概率
⑶ 已知第二次摸到了红球，求第一次摸到的是红球的概率。验后概率
解：⑴ P(A)=3/5，这就是验前概率；
⑵ P(B)=P(A)P(B|A)+P(A逆)P(B|A逆)=3/5
⑶ P(A|B)=P(A)P(B|A)/P(B)=1/2，这就是验后概率。
随机变量及其意义
引入随机变量是为了把实验结果用数字化的方式来表达，$X=x$实际上对应着样本空间中的事件，其代表了编码为数值$x$对应的那个事件。随机变量的本质实际上是一个函数，$X:S - R$将文字描述的事件映射为便于数学表达和运算的数字。比如“骰子投掷得到大于3这个点数”这是一个事件，文字描述非常繁琐，但是如果用X这个随机变量代表骰子点数的话，则很容易得到用随机变量表达式替代的等价事件。($X>3$)。再比如下面的$X$映射函数
$X(骰子点数为5)=5，X(骰子点数为1)=1$
随机变量的概率分布律(概率密度)对应着事件的概率，求一个事件的概率就等于求随机变量取某些值的概率，
这样就将随机事件及其概率的研究就演变为随机变量及其取值规律的研究。
随机变量的种类
按照随机变量映射取值的形式分类为离散随机变量和连续随机变量
离散随机变量的值是有限的或可数的或无限个离散数字；$X(迟到)=0,X(早退)=1,X(正常)=2,X(缺席)=3$。甚至即便映射后的值可能是无数多个，但是只要其值是一个离散的数字也归类为离散随机变量，比如$X(经过多少次实验才能最终成功)=1，2，3，。。。$
连续型随机变量：只要映射后的数字为不可数的无穷多个数值，那么就是连续随机变量。比如$X(幸运之轮的结果)=(0,1)$
可数vs不可数
比如偶数集合$\{2,4,6,8,10,12....\}$虽然是无穷大， 但是只要你有恒心，该集合中的任何一个数字总归能被数到；
再比如$(0,1)$之间的实数的集合，你是无法穷尽数到所有的数字的，这个就是不可数
概率累积函数CDF
$F_X(x) = P(X \leq x)$
CDF很重要的作用是计算随机变量落在某个范围内的概率
CDF有个重要的特点是$- \infty$为0，在$+ \infty$为1
离散型概率分布列(PMF)
对于离散型变量，PMF描述变量在各个离散值上的概率分布
常用的离散分布
0-1分布(两点分布，伯努利分布) $X\sim B(1,p)$ 1 表示为1次伯努利实验， p为成功的概率
概率密度
$$P(X=k) = p^k(1-p)^{1-k} , k=0,1, 0 < p <1$$
二项分布（Binomial distribution）($X\sim B(n,p)$)
概率密度：
$$P(X = k) = \binom{n}{k}p^kq^{n-k}, k = 0,1,...,n, 0 < p <1 ,q = 1 - p$$
注意当n=1的时候二项分布就成为两点分布,也就是只做1次伯努利实验其结果就是两点分布
描述有放回抽样
概率累计函数(CDF):
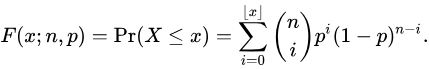
二项分布描述n重伯努利试验中"成功"出现次数X的概率分布
泊松分布($X\sim P(\lambda)$)
$$P(X=k)= \frac{\lambda ^ke^{-\lambda}}{k!} , \lambda > 0, k = 0,1,2,...$$
参数λ是单位时间（或单位面积）内随机事件的平均发生率
它多出现在当X表示在一定的时间或空间内出现的事件个数这种场合。在一定时间内某交通路口所发生的事故个数，是一个典型的例子。
常见应用：某电话交换台收到的呼叫、来到某公共汽车站的乘客、某放射性物质发射出的粒子、显微镜下某区域中的白血球等等，以固定的平均瞬时速率λ（或称密度）随机且独立地出现时，那么这个事件在单位时间（面积或体积）内出现的次数或个数就近似地服从泊松分布P(λ)。
泊松分布可作为二项分布的极限而得到。一般的说，若
,其中n很大，p很小，因而
不太大时，X的分布接近于泊松分布
。
几何分布($X\simeq G(p)$)
$$P(X=k)= q^{k-1}p , \lambda > 0, k = 0,1,2,..., 0 < p < 1, q = 1-p$$
常见应用：在伯努利实验中，设每次实验成功的概率均为p($0<p<1$),独立重复实验直到首次出现成功为止，所需实验的次数X服从几何分布
几何分布具有无记忆性的特点$P(X> n + m|X>n) = P(X>m)$
超几何分布描述不放回抽样，当抽样数很大而抽样数n很小时可以用二项分布来逼近超几何分布
数理统计中常用做置信估计的概率分布模型:卡方分布，t分布, F分布
卡方分布
分布（chi-square distribution），其中参数 
称为自由度，正如正态分布中均数或方差不同就是另一个正态分布一样，自由度不同就是另一个
分布。记为 
或者 
（其中 
， 
为限制条件数）。
很大时， 分布近似为正态分布。
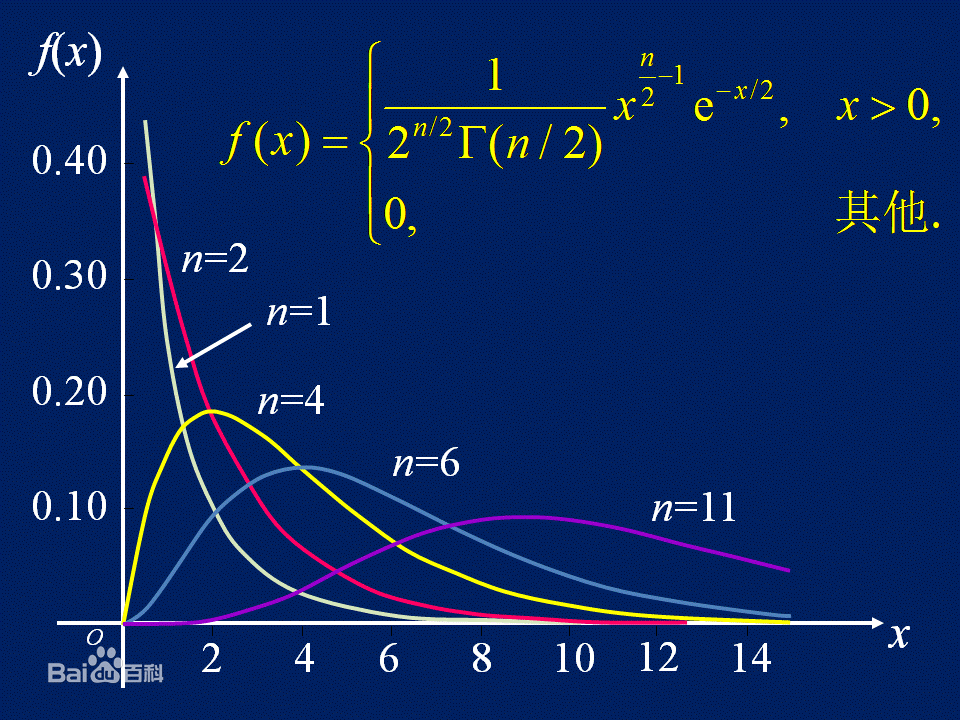
t分布
如果一个随机变量是由一个服从正态分布的随机变量除以一个服从卡方分布的变量组成的，则该变量服从t分布，t分布是正态分布的小样本形态。
比如对于正态分布样本的均值变换为$t = \frac{\bar X - \mu}{S_{\bar X}} = \frac{\bar X - \mu}{S/ \sqrt n}$后就服从自由度为n-1的t分布
t分布是于自由度$v$有关的一组曲线，随着$v$的增大接近标准正态分布
F分布
设$X,Y$是两个相互独立的遵循卡方分布的随机变量$X \sim \chi ^2(n_1),Y \sim \chi ^2(n_2)$,则
$F = \frac{X/n_1}{Y/n_2} = \frac {n2}{n1} \cdot \frac {X}{Y} \sim F(n_1,n_2)$服从自由度为n1,n2的F分布
为什么我们要学习概率分布？
1. 很多事物背后的概率模型($P(X)$)我们是不知道的，因此很难对这类事物的概率做有效研究；
2. 但是如果我们对事物的运作方式及其本质弄清楚后，我们会发现那些事物可能与已知的概率分布的本质相同或者接近，那么我们便可以采用该已知的概率分布去近似模拟该事物的运作，
3.利用我们已知熟悉的概率分布模型去计算各式各样事件的概率
连续型随机变量的概率密度
和离散型随机变量的PMF对应，连续型变量我们用PDF：概率密度来描述概率的分布。
连续性随机变量几个常用概率分布
均匀分布(等可能)(Uniform) $X\sim U(a,b) $
$$f(x) = \left\{\begin{matrix}\frac{1}{b-a},a\leq x\leq b\\ 0, other \end{matrix}\right.$$
指数分布$X\sim E(\lambda)$
$$f(x) = \left\{\begin{matrix} \lambda e^{-\lambda x},0 < x \\ 0, 0 \leq x \end{matrix}\right.$$
指数分布往往用于描述"寿命"衰减等现象
正态分布$X\sim N(\mu, \sigma ^2)$
$$f(x) = \frac{1}{\sigma \sqrt{2\pi }}e^{-\frac{(x-\mu )^2}{2\sigma ^2}} ,( - \infty < x < + \infty )$$
当$\mu=0, \sigma =1$时为标准正态分布。标准正态分布具有以下特殊性质:
1. 概率密度函数是偶函数$\varphi (-x) = \varphi (x) $
2. 概率分布函数具有以下性质$\phi (-x) = 1 - \phi (x)$
一般正态分布$X\sim N(\mu, \sigma ^2)$的CDF函数$F(x)$和标准正态分布的CDF函数$\phi(x)$之间的关系为:
$$F(x) = \phi(\frac{x-\mu}{\sigma})$$
也就是说任何普通正态分布都可以变换为标准正态分布，这一点在机器学习的特征变换中经常使用
$$\frac{X-\mu}{\sigma} \sim N(0,1)$$
我们也可以利用这一点来计算正态分布某范围的概率值：
$若X \sim N(\mu,\sigma^2), \forall a < b，有:$
$P(a <X<b)=F(b) - F(a) = \phi(\frac{b-\mu}{\sigma}) - \phi(\frac{a-\mu}{\sigma})$
经过变换后，我们只要查找标准正态分布表就可以求得对应的概率了。
正态分布下随机变量$X$的中心化/标准化变换:
中心化:
$X_* = X-E(X); E(X_*) = 0, D(X_*) = D(X)$
标准化:
$X_* = \frac{X-E(X)}{\sqrt {D(X)}}; E(X_*) = 0, D(X_*) = 1$
正态分布的应用：
测量一个物体长度的误差，打靶偏离中心点的距离，电子管噪声电压和电流，飞机材料的疲劳应力等
随机变量函数$g(X)$的概率密度
我们这里只罗列一个正态分布变量的线性变换函数的概率密度性质，非常重要，可以直接使用:正态分布的随机变量线性变换后依然服从正态分布!
若$ X \sim N(\mu,\sigma^2)$则，
$Y=aX+b \sim N(a\mu+b,a^2\sigma^2)$
可以推广n个独立的正态分布变量的线性组合仍为正态分布，即:
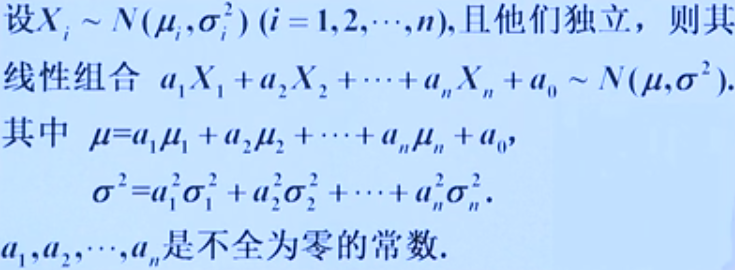
下面给出随机变量函数的概率密度计算一般方法（适用于连续性和离散型变量）
多纬联合分布率
很多随机现象需要多个随机变量来描述，比如打靶时，命中点的位置需要用坐标X,Y来表示，研究天气现象时，描述天气需要气温X，气压Y，风速Z等变量来表示。
二维随机变量$(X,Y)$的分布函数
$F(X,Y)=P(X\leq x, Y \leq y) -\infty < x,y<+\infty$
几何意义:
边缘分布函数:
我们只列出一个实用的离散型二维随机变量联合分布列，可以看到两个变量的表横向纵向概率之和都为0，这在pandas中的crosstab考察概率是相对应的。
$p_{X,Y}(x,y)= P(X=x, Y =y)$
二维正态分布$(X,Y) \sim N(\mu_1,\mu_2,\sigma_1^2,\sigma_2^2,\rho )$
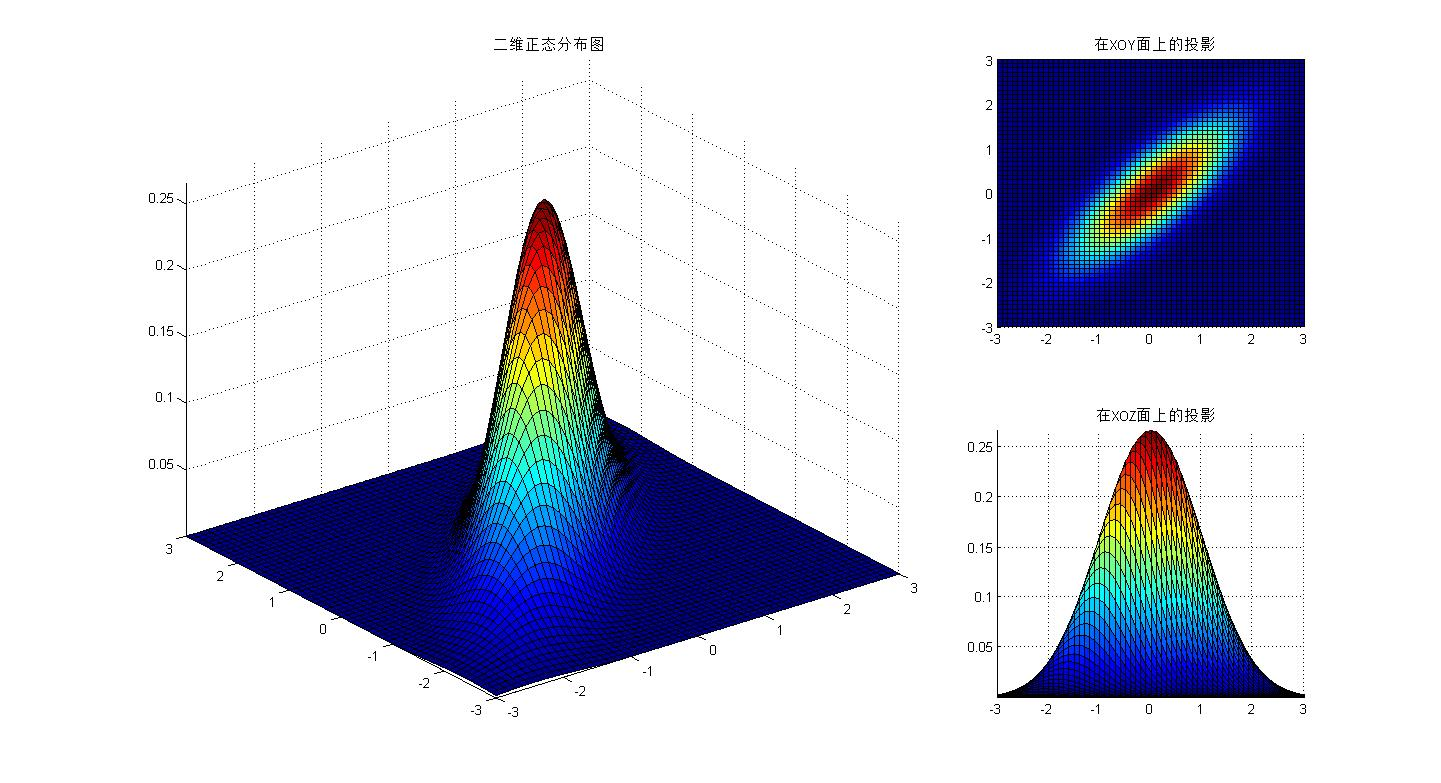
统计量
统计量依赖且只依赖于样本x1,x2,…xn；它不含总体分布的任何未知参数。从样本推断总体（见统计推断）通常是通过统计量进行的。例如x1,x2，…，xn是从正态总体N(μ,1）（见正态分布）中抽出的简单随机样本，其中总体均值（见数学期望）μ是未知的，为了对μ作出推断，计算样本均值。可以证明，在一定意义下，包含样本中有关μ的全部信息，因而能对μ作出良好的推断。这里只依赖于样本x1,x2，…，xn，是一个统计量。
期望($E[X]$）和均值
均值是一个统计学概念，是后验数据，是对统计得到的样本取均值；
期望是概率与数理统计的概念，是先验数据，是根据经验的概率分布“预测"的样本均值。
如果我们的概率分布是正确的假设的话，那么当实验次数足够大时，样本的均值就趋向于期望。
数学期望的计算性质
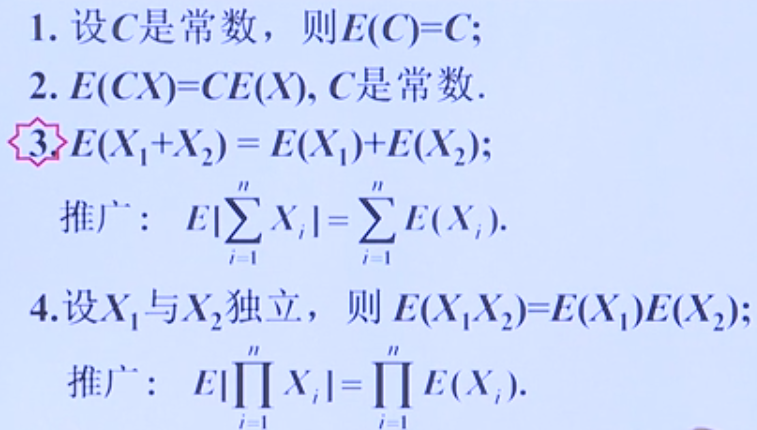
离散型随机变量的期望：
$$E[X]=\sum p_ix_i$$
如果说概率是频率随样本趋于无穷的极限，那么期望就是平均数随样本趋于无穷的极限
常用分布的数学期望和方差:
连续型随机变量的期望：
$$E(X) = \int_{-\infty }^{+\infty}x \cdot f(x)dx$$
可以看到实际上就是用x代替离散型定义的$x_i$，用$f(x)dx$代替离散型定义的$p_i$,其中$f(x)$是随机变量x的概率密度函数
随机变量函数的期望
设$Y = g(x)$,则：
1. 如果x是离散型变量:
$$E(Y)=E[g(X)]=\sum g(x_i)p_i$$
2. 如果x是连续型变量:
$$E(Y) = E(g(x)) = \int_{-\infty }^{+\infty}g(x) \cdot f(x)dx$$
方差$D(X)$
定义：$D(X) = E[X-E(X)]^{2} $ 也就是说方差是$[X-E(X)]^{2}$的数学期望(均值)
常用计算公式 $D(X) = E(X^{2}) - (E(X))^{2}$
方差$D(X)$的性质
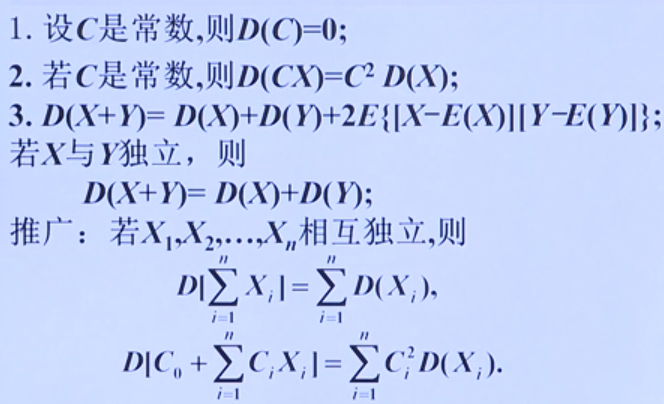
协方差及相关系数
先假设有两个随机变量$X,Y及其均值分别为\bar X, \bar Y$,这两个随机变量容量为n的样本，我们由$X,Y$构造两个向量(可以这么认为，对于随机变量组成的向量，其均值才是原点):
$\vec{x} = (X_1-\bar X, X_2-\bar X,..,X_i - \bar X,..X_n-\bar X); \vec{y} = (Y_1-\bar Y, Y_2-\bar Y,..,Y_i - \bar Y,..Y_n-\bar Y)$
协方差是随机变量的波动之乘积的期望
样本方差
$S_X^{2} = \frac{1}{n-1}\sum_{i=1}^{n}(X_i-\bar X)^2 = \frac{\vec{x} \cdot \vec{x}}{n-1}$
$S_Y^{2} = \frac{1}{n-1}\sum_{i=1}^{n}(Y_i-\bar Y)^2 = \frac{\vec{y} \cdot \vec{y}}{n-1}$
样本协方差:
样本计算式:$S_{XY} = \frac{1}{n-1}\sum_{i=1}^{n}(X_i-\bar X)(Y_i-\bar Y) = \frac{\vec{x} \cdot \vec{y}}{n-1}$
理论定义式:$Cov(X,Y) = E([X-E(X)][Y-E(Y)]) = E(XY) - E(X)E(Y)$
若X,Y互相独立，则$S_{XY},Cov(X,Y) = 0$ ，协方差为0；$S_{XY},Cov(X,Y) > 0 $ 则称X,Y是正相关($X - \bar X与 Y- \bar Y$同大同小的概率比较大);若$ S_{XY},Cov(X,Y) < 0 $ 则称X,Y是负相关（$X - \bar X与 Y- \bar Y$大小相反的概率比较大）
若协方差为0，不能推出$X,Y$独立，也就是说虽然线性无关，但是有可能非线性方式相关。独立是一个强条件，是没有任何关系
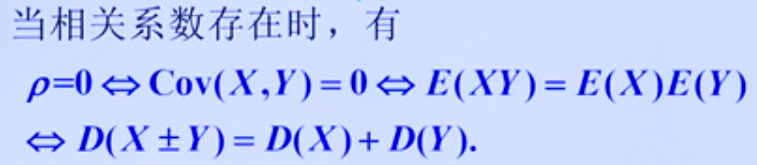
特征工程中，如果两个变量的协方差绝对值比较大的话，则说明X,Y是线性相关的，那么就应该剔除掉一个，否则出现"多重共线性"
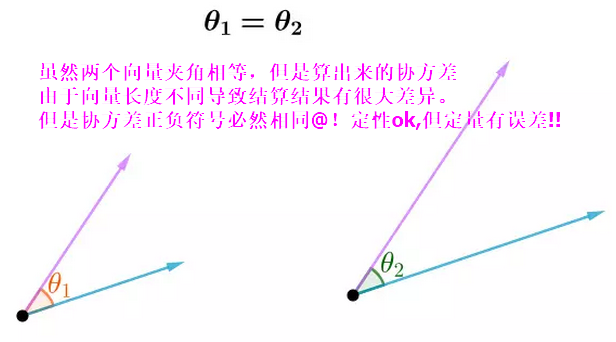
一般来说通过协方差就能描述两个向量之间的关系了，但是由于协方差的值会受到向量长度本身的影响，因此很难判断其相关的程度，为解决该问题，我们引入相关系数这个概念以消除向量长度的影响。
给定一个特征向量$(X_1,X_2,...,X_n)$两两计算其协方差会形成一个nxn的协方差矩阵，这个矩阵在PCA降纬时使用.
$$C= \begin{bmatrix} c_{11} & c_{12} & ... & c_{1n}\\ c_{21} & c_{22} & ... & c_{2n}\\ ... & ... & ... & ...\\ c_{n1} & c_{n2} & ... & c_{nn} \end{bmatrix}$$
相关系数:
样本计算式:$r = \frac{\vec{x}\cdot \vec{y}}{|\vec{x}|\times |\vec{y}|}=cos(\theta)$
从这个定义中我们看出，相关系数实际上是描述$X,Y$分别相均值平移后的向量夹角的余弦值，范围为$(-1,+1)$，如果为0表示向量正交垂直，说明两向量无关，如果为1，则线性正相关，如果为-1则线性负相关。
相关系数又称为标准协方差
理论定义式:$\rho _{XY} = \frac{Cov(X,Y)}{\sqrt{D(X)}\sqrt {D(Y)}}$
当$\rho _{XY}$ 为1时，说明完全线性相关，如果比较小，则说明线性相关程度越低
散点图和相关系数值的直观映射
协方差的性质
- $cov(X,Y)=cov(Y,X)$
- $cov(X,C) = 0$
- $cov(kX,lY) = klcov(X,Y)$
- $cov(\sum_{i=1}^{m} X_i, \sum_{j=1}^{n} Y_j) = \sum_{i=1}^{m}\sum_{j=1}^{n}cov(X_i,Y_j)$
- $D(X\pm Y) = D(X)+D(Y)\pm 2E((X-E(X)(Y- E(Y)) = D(X)+D(Y)\pm 2 \rho (X,Y) \sqrt {D(X)D(Y)}$
两个随机变量的相关vs独立
一般情况下不相关是无法得出独立的结论的，但是，对于二维正态分布$(X,Y) \sim N(\mu_1,\mu_2,\sigma_1^2,\sigma_2^2,\rho )$，不独立和不相关是等价的！！！
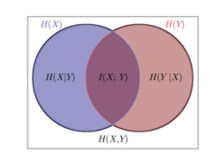
互信息$I(X,Y)$
https://baike.baidu.com/item/%E4%BA%92%E4%BF%A1%E6%81%AF
http://www.cnblogs.com/liugl7/p/5385061.html
决定系数(coefficient of Determination)和相关系数(correlation of Coefficient)
https://blog.csdn.net/danmeng8068/article/details/80143306
先看以下几个定义：
a. Sum of Squares Due to Error
b. total sum of squares
c. sum of squares due to regression
以上三者之间存在以下关系:
决定系数用于判断回归方程的拟合程度，也就是通过model得出的因变量的变化有百分之多少可以由自变量来解释，从而判断拟合的程度。在Y的总平方和中，由X引起的平方和所占的比例，记为$R^{2}$ (R的平方). 当$R^{2}$接近于1时，表示模型参考价值越高，
相关系数：测试因变量自变量之间的线性关系的，也就是说自变量发生变化时，因变量的变化情况如何
似然函数,损失函数和最大似然估计
https://www.cnblogs.com/hejunlin1992/p/7976119.html
似然函数是关于统计模型中的参数函数，表示模型参数的似然性。往往通过求解当似然函数最大时的参数作为最优参数
损失函数则是机器学习中用于度量模型效果的函数，他是模型参数的函数，给定数据集，只和模型参数有关。
sk-learn vs statemodel
https://blog.thedataincubator.com/2017/11/scikit-learn-vs-statsmodels/
dummy variable trap - one-hot encoding
我们知道，对于categorical类型的feature必须编码成适合于应用到机器学习模型中去的数值，而编码的方法常见的就是sklearn的one-hot encoding.但是我们必须注意的是对于有n个类别值的变量编码时只能使用n-1个dummy variable,否则将发生多重共线性问题！
sklearn dummy编码已经考虑到这个场景。one-hot编码也应该有相关参数来控制。在实际工程实践中，我们应该选择占比最高的类别作为基准类别，否则即使使用了n-1变量，也会残存比较严重的共线性问题。比如a,b,c,d四个类别，a只有1%的占比，那么如果选择a为基准，参与运算的为b,c,d三个dummy variable,那么绝大部分时间里面b+c+d =1 存在线性问题！
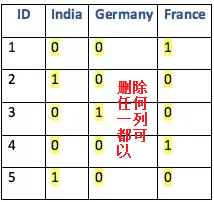
有序定性变量的Redit scoring
上面我们谈到通过dummy encoding或者one-hot encoding,我们很方便有效地完成了category类型feature的数值化编码，但是如果我们的category变量本身是有序或者出现频率大不相同的情况，比如成绩不及格，及格，良好，优秀，杰出，这些类别值本身是有一定的顺序含义的，仅仅dummy encoding可能会丢失这些有价值的信息。再比如虽然对于男女这个cate变量本身不具有序列意义，但是如果数据集中男生比例67%，女生比例33%，那么可以使用Redit scoring编码：
$B_i = \sum {_{j<i}p_j} - \sum {_{j>i}p_j}$
最后得到$B_{male} = -0.33, B_{female} = 0.67$
