廒睿骋隺冀
ARC151
A
直接看\(S,T\)不同的位置,然后贪心填就行了
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=2e5+5;
int n;
char S[MAXN];
char T[MAXN];
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&n);
scanf("%s",S+1);
scanf("%s",T+1);
int Cnt=0;
for(int i=1;i<=n;i++)
{
if(S[i]!=T[i])
{
++Cnt;
}
}
if(Cnt&1)
{
printf("-1");
return 0;
}
int Rs=Cnt/2,Rt=Cnt/2;
for(int i=1;i<=n;i++)
{
if(S[i]==T[i])
{
printf("0");
}
else
{
if(S[i]=='0')
{
if(Rs)
{
Rs--;
printf("0");
}
else
{
printf("1");
}
}
else
{
if(Rt)
{
Rt--;
printf("0");
}
else
{
printf("1");
}
}
}
}
}
B
直接枚举第一个不等的位置,前面相等的用斌茶几维护一下连通块个数即可,联通块除了枚举的点之间互不影响
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MOD=998244353;
const int MAXN=2e5+5;
int Pow(int a,int b,int p)
{
int res=1;
int base=a;
while(b)
{
if(b&1)
{
res=((long long)res*base)%p;
}
base=((long long)base*base)%p;
b>>=1;
}
return res;
}
int n,m;
int p[MAXN];
int fa[MAXN];
int find(int x)
{
if(fa[x]==x)
{
return fa[x];
}
fa[x]=find(fa[x]);
return fa[x];
}
int Cnt;
void unionn(int i,int j)
{
int ex=find(i);
int ey=find(j);
if(ex!=ey)
{
fa[find(i)]=find(j);
Cnt--;
}
}
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d %d",&n,&m);
Cnt=n;
int inv2=(MOD-MOD/2);
for(int i=1;i<=n;i++)
{
scanf("%d",&p[i]);
fa[i]=i;
}
int Res=0;
for(int i=1;i<=n;i++)
{
if(find(i)!=find(p[i]))
{
if(Cnt>1)
{
int Ni=Pow(m,Cnt-2,MOD);
Ni=((long long)Ni*m)%MOD;
Ni=((long long)Ni*(m-1))%MOD;
Ni=((long long)Ni*inv2)%MOD;
Res=((long long)Res+Ni)%MOD;
}
}
unionn(i,p[i]);
}
printf("%d\n",Res);
}
C
直接套\(sg\)
已经填的两个数\(x,y\)之间\(sg=[x=y]\),手完一下就出来了
两边的空的\(k\), \(sg=k-1/(n-k)\)
Show Code
// #include<bits/stdc++.h>
// using namespace std;
// int Sg[105][2][2];
// int main()
// {
// // freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
// Sg[0][1][1]=Sg[0][0][0]=1;
// for(int i=1;i<=10;i++)
// {
// for(int l=0;l<=1;l++)
// {
// for(int r=0;r<=1;r++)
// {
// vector<int>V;
// for(int k=1;k<=i;k++)
// {
// V.push_back(Sg[k-1][l][0]^Sg[i-k][0][r]);
// V.push_back(Sg[k-1][l][1]^Sg[i-k][1][r]);
// }
// sort(V.begin(),V.end());
// unique(V.begin(),V.end());
// int Mex=V.size();
// for(int k=0;k<V.size();k++)
// {
// if(V[k]!=k)
// {
// Mex=k;
// break;
// }
// }
// Sg[i][l][r]=Mex;
// printf("%d %d %d %d\n",i,l,r,Mex);
// }
// }
// }
// }
#include<bits/stdc++.h>
using namespace std;
const int MAXN=2e5+5;
long long n;
int m;
long long x;
int y;
pair<long long,int>V[MAXN];
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%lld %d",&n,&m);
if(m==0)
{
if(n&1)
{
printf("Takahashi");
}
else
{
printf("Aoki");
}
return 0;
}
for(int i=1;i<=m;i++)
{
scanf("%lld %d",&x,&y);
V[i]=make_pair(x,y);
}
long long sg=0;
for(int i=1;i<m;i++)
{
if(V[i].second==V[i+1].second)
{
sg^=1;
}
}
sg^=(V[1].first-1);
sg^=(n-V[m].first);
if(sg)
{
printf("Takahashi");
}
else
{
printf("Aoki");
}
}
D
酱汁了/kk
首先不同位之间的操作互不影响,这个性质很关键
证明的话手完一下就可以了,你会发现建出来的图对应路径是一定的
然后相同位的顺序不能换,但我们就可以直接维护\(f_{op1,op2}\)表示\(op1\)中\(op2\)的系数
然后就完了??
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=3e5+5;
const int MOD=998244353;
int n;
int a[MAXN];
int b[MAXN];
int q;
int x,y;
vector<int>Rec[35];
int f[2][2];
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d %d",&n,&q);
for(int i=0;i<(1<<n);i++)
{
scanf("%d",&a[i]);
}
while(q--)
{
scanf("%d %d",&x,&y);
Rec[x].push_back(y);
}
for(int i=0;i<n;i++)
{
f[0][0]=1;
f[1][1]=1;
f[0][1]=0;
f[1][0]=0;
for(int j=0;j<Rec[i].size();j++)
{
int op=Rec[i][j];
f[op^1][op]=((long long)f[op^1][op]+f[op][op])%MOD;
f[op^1][op^1]=((long long)f[op^1][op^1]+f[op][op^1])%MOD;
}
for(int j=0;j<(1<<n);j++)
{
int op=((j>>i)&1);
b[j]=((long long)a[j]*f[op][op])%MOD;
b[j]=((long long)b[j]+((long long)a[j^(1<<i)]*f[op][op^1]))%MOD;
}
for(int j=0;j<(1<<n);j++)
{
a[j]=b[j];
}
}
for(int i=0;i<(1<<n);i++)
{
printf("%d ",a[i]);
}
}
E
经典E比D简单
不难看出就是找个最长公共子串,这个\(Hash\)一下就好了
但如果没有的情况有点麻烦,我最开始觉得得用\(KMP\)枚举每个位置再线段树维护一下
不过似乎直接建\(a_i\rightarrow a_{i+1}\)跑多元最短路即可
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=2e5+5;
int n,p,q;
int a[MAXN];
int b[MAXN];
int c[MAXN];
const unsigned long long p1=998244353;
const unsigned long long p2=1e9+7;
map<unsigned long long,int>vis1,vis2;
unsigned long long Mul1[MAXN];
unsigned long long Mul2[MAXN];
unsigned long long Hashb1[MAXN];
unsigned long long Hashb2[MAXN];
unsigned long long Hashc1[MAXN];
unsigned long long Hashc2[MAXN];
unsigned long long Getb1(int l,int r)
{
return Hashb1[r]-Hashb1[l-1]*Mul1[r-l+1];
}
unsigned long long Getc1(int l,int r)
{
return Hashc1[r]-Hashc1[l-1]*Mul1[r-l+1];
}
unsigned long long Getb2(int l,int r)
{
return Hashb2[r]-Hashb2[l-1]*Mul2[r-l+1];
}
unsigned long long Getc2(int l,int r)
{
return Hashc2[r]-Hashc2[l-1]*Mul2[r-l+1];
}
bool check(int mid)
{
vis1.clear();
vis2.clear();
for(int i=1;i+mid-1<=p;i++)
{
int l=i;
int r=i+mid-1;
vis1[Getb1(l,r)]=1;
vis2[Getb2(l,r)]=1;
}
for(int i=1;i+mid-1<=q;i++)
{
int l=i;
int r=i+mid-1;
if(vis1[Getc1(l,r)]&&vis2[Getc2(l,r)])
{
return 1;
}
}
return 0;
}
int Vis[MAXN];
int dis[MAXN];
vector<int>g[MAXN];
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&n);
Mul1[0]=Mul2[0]=1;
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
Mul1[i]=Mul1[i-1]*p1;
Mul2[i]=Mul2[i-1]*p2;
}
scanf("%d",&p);
for(int i=1;i<=p;i++)
{
scanf("%d",&b[i]);
Hashb1[i]=Hashb1[i-1]*p1+b[i];
Hashb2[i]=Hashb2[i-1]*p2+b[i];
}
scanf("%d",&q);
for(int i=1;i<=q;i++)
{
scanf("%d",&c[i]);
Hashc1[i]=Hashc1[i-1]*p1+c[i];
Hashc2[i]=Hashc2[i-1]*p2+c[i];
}
int l=1;
int r=min(p,q);
int Key=-1;
while(l<=r)
{
int mid=(l+r)>>1;
if(check(mid))
{
l=mid+1;
Key=mid;
}
else
{
r=mid-1;
}
}
if(Key!=-1)
{
printf("%d\n",p+q-2*Key);
}
else
{
for(int i=1;i<=n;i++)
{
if(i<n)
{
g[a[i]].push_back(a[i+1]);
g[a[i+1]].push_back(a[i]);
}
dis[i]=0x3f3f3f3f;
}
queue<int>Q;
for(int i=1;i<=p;i++)
{
Q.push(b[i]);
dis[b[i]]=0;
}
while(Q.size())
{
int temp=Q.front();
Q.pop();
for(int i=0;i<g[temp].size();i++)
{
int v=g[temp][i];
if(dis[v]!=0x3f3f3f3f)
{
continue;
}
dis[v]=dis[temp]+1;
Q.push(v);
}
}
int Mini=0x3f3f3f3f;
for(int i=1;i<=q;i++)
{
Mini=min(Mini,dis[c[i]]);
}
printf("%d\n",2*Mini+p-1+q-1);
}
}
ARC152
小偷一个懒🙃
A
贪心地放即可
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=2e5+5;
int n;
int a[MAXN],L;
signed main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d %d",&n,&L);
int Cnt1=0,Cnt2=0;
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
if(a[i]==2)
{
if(L<2)
{
printf("No");
return 0;
}
L-=3;
}
else
{
L-=2;
}
}
printf("Yes");
}
B
结论题
如果第一次相遇的地方是\(p\),则第二次相遇理论上应该在\(L-p\)的地方相遇
直接让起点作为第一次相遇的地方即可
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=2e5+5;
int n;
int a[MAXN];
int L;
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d %d",&n,&L);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
}
int Res=1e9;
for(int i=1;i<=n;i++)
{
int to=L-a[i];
int Lw=lower_bound(a+1,a+1+n,to)-a;
if(Lw!=n+1)
{
Res=min(Res,a[Lw]-to);
}
int Up=upper_bound(a+1,a+1+n,to)-a-1;
if(Up)
{
Res=min(Res,to-a[Up]);
}
}
printf("%lld\n",2ll*(L+Res));
}
C
有点意思的题
首先这个问题相当于在数轴上选一个基点反转
因此最大值最小值的距离是不变的
那个不能翻到负数的条件可以多次反转最大值到极远处
考虑反转一次一次\(i\)对答案的增量\(b_i=|a_n+a_1-2a_i|\)
这个可以看作\(a_n-a_1+(a_1+\sum\limits k_ib_i)\),这个式子最小正整数为\(a_n-a_1+(a_1\bmod \gcd(b_i))\)
Show Code
#include<bits/stdc++.h>
using namespace std;
int Abs(int x)
{
return x>0?x:-x;
}
const int MAXN=2e5+5;
int n;
int a[MAXN];
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
}
int d=0;
int g=0;
for(int i=1;i<=n;i++)
{
g=__gcd(g,Abs(a[1]+a[n]-2*a[i]));
}
printf("%d",a[n]-a[1]+(a[1]%g));
}
D
考虑\(x\rightarrow (x+k)\bmod n\)
这样会连出来\(\gcd(n,k)\)个环
然后一张图一目了然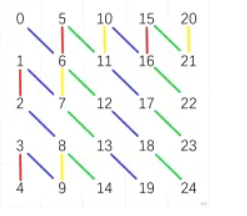
蓝红是选连的边,绿黄是产生的边
特判一下一行的情况
Show Code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN=2e5+5;
int n,k;
signed main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%lld %lld",&n,&k);
if((n%2==0))
{
printf("-1");
return 0;
}
int Cnt=(__gcd(n,k));
printf("%lld\n",n/2);
if(Cnt==1)
{
for(int i=0;i<n-1;i+=2)
{
printf("%lld %lld\n",((long long)i*k)%n,((long long)(i+1)*k)%n);
}
return 0;
}
int Len=n/Cnt;
for(int i=0;i<Cnt-1;i++)
{
for(int j=0;j<Len-1;j+=2)
{
printf("%lld %lld\n",(i+j*k)%n,((i+1)+(j+1)*k)%n);
}
}
for(int i=1;i<Len;i+=2)
{
printf("%lld %lld\n",(i*k)%n,(i*k+1)%n);
}
for(int i=1;i<Cnt-1;i+=2)
{
printf("%lld %lld\n",i%n,(i+1)%n);
}
}
E
性质题
首先所有数异或和为\(0\)
然后对于一个数\(i\),左边的异或和为\(L_i\),则右边的为\(L_i\oplus a_i\)
如果设\(p\)为前缀和则左边为\(p_{i-1}\),右边为\(p_i\)
考虑两个小球合并,对于其他球\(L,R\)不变,而对于合并的球,\(L=p_{i-1},R=p_{i+1}\),这就等同于将球\(i\)删除
再考虑何时可删,实际上就是\(p_i>p_{i-1}\)且\(p_i>p_{i+1}\)的时候
实际上经过多次操作后会变成一个下凸函数,只有当函数为一条线时会停止
这就等同于\(Z\le Z\oplus p_i\),这等价于\(Z\)在\(p_i\)的最高位为\(0\)
Show Code
#include<bits/stdc++.h>
using namespace std;
int n;
int a[(1<<18)+5];
int p[(1<<18)+5];
int vis[25];
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<(1<<n);i++)
{
scanf("%d",&a[i]);
p[i]=p[i-1]^a[i];
for(int j=n-1;j>=0;j--)
{
if((p[i]>>j)&1)
{
vis[j]=1;
break;
}
}
}
int Cnt=0;
for(int i=0;i<n;i++)
{
if(!vis[i])
{
++Cnt;
}
}
printf("%d",(1<<Cnt));
}
ARC153
A
直接枚举所有的美丽数即可
Show Code
#include<bits/stdc++.h>
using namespace std;
vector<int>V;
signed main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
for(int i1=1;i1<=9;i1++)
{
int i2=i1;
for(int i3=0;i3<=9;i3++)
{
for(int i4=0;i4<=9;i4++)
{
for(int i5=0;i5<=9;i5++)
{
int i6=i5;
for(int i7=0;i7<=9;i7++)
{
for(int i8=0;i8<=9;i8++)
{
int i9=i7;
int Nt=(((((((((i1*10)+i2)*10+i3)*10)+i4)*10+i5)*10+i6)*10+i7)*10+i8)*10+i9;
V.push_back(Nt);
}
}
}
}
}
}
//cerr<<V.size()<<endl;
sort(V.begin(),V.end());
int N;
scanf("%d",&N);
printf("%d\n",V[N-1]);
}
B
平衡树搞一下即可
Show Code
#include<bits/stdc++.h>
#define ls Tree[p].child[0]
#define rs Tree[p].child[1]
using namespace std;
const int MAXN=5e5+5;
struct FHQ_Tree{
int Size;
int cnt;
int child[2];
int val;
int key;
int lazy_roll;
};
vector<int>a,b;
struct FHQ{
FHQ_Tree Tree[MAXN];
int cnt_node=0;
int root;
int New(int val)
{
Tree[++cnt_node].key=rand();
Tree[cnt_node].cnt=1;
Tree[cnt_node].Size=1;
Tree[cnt_node].val=val;
return cnt_node;
}
void push_up(int p)
{
Tree[p].Size=Tree[ls].Size+Tree[rs].Size+Tree[p].cnt;
}
void RL(int p)
{
swap(ls,rs);
Tree[p].lazy_roll^=1;
}
void push_down(int p)
{
if(Tree[p].lazy_roll)
{
// swap(ls,rs);
if(ls)
{
RL(ls);
}
if(rs)
{
RL(rs);
}
Tree[p].lazy_roll=0;
}
}
void Split(int p,int val,int &x,int &y)
{
if(!p)
{
x=0;
y=0;
return;
}
push_down(p);
if(Tree[ls].Size+Tree[p].cnt<=val)
{
x=p;
Split(rs,val-Tree[ls].Size-Tree[p].cnt,rs,y);
}
else
{
y=p;
Split(ls,val,x,ls);
}
push_up(p);
}
int merage(int x,int y)
{
if((!x)||(!y))
{
return x+y;
}
if((Tree[x].key)<(Tree[y].key))
{
push_down(x);
Tree[x].child[1]=merage(Tree[x].child[1],y);
push_up(x);
return x;
}
else
{
push_down(y);
Tree[y].child[0]=merage(x,Tree[y].child[0]);
push_up(y);
return y;
}
}
void insert(int x,int val)
{
int lx,rx;
Split(root,x,lx,rx);
root=merage(merage(lx,New(val)),rx);
return;
}
void roll(int l,int r)
{
int lx,zx,rx;
Split(root,l-1,lx,rx);
Split(rx,r-l+1,zx,rx);
// Tree[zx].lazy_roll^=1;
RL(zx);
root=merage(merage(lx,zx),rx);
return;
}
void print(int p)
{
if(!p)
{
return;
}
push_down(p);
print(ls);
// printf("%d ",);
a.push_back(Tree[p].val);
print(rs);
}
}tree1,tree2;
int n,m,q;
int l,r;
int x,y;
string V[MAXN];
int main()
{
srand(time(0));
scanf("%d %d",&n,&m);
for(int i=1;i<=n;i++)
{
tree1.insert(i-1,i);
}
for(int i=1;i<=m;i++)
{
tree2.insert(i-1,i);
}
for(int i=1;i<=n;i++)
{
cin>>V[i];
}
scanf("%d",&q);
while(q--)
{
scanf("%d %d",&x,&y);
tree1.roll(1,x);
tree1.roll(x+1,n);
tree2.roll(1,y);
tree2.roll(y+1,m);
}
tree2.print(tree2.root);
b=a;
a.clear();
tree1.print(tree1.root);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
int Keyi=a[i-1];
int Keyj=b[j-1];
printf("%c",V[Keyi][Keyj-1]);
}
printf("\n");
}
// for(int i=1;i<=n;i++)
// {
// printf("%d ",a[i-1]);
// }
// printf("\n");
// for(int i=1;i<=m;i++)
// {
// printf("%d ",b[i-1]);
// }
}
C
最后一个可以作为调整的,让它是\(-1\),然后这里我们可以尽量让\(+\)的比\(-\)的多即可
然后这里先构造为前面一个比后面刚好小\(1\)
然后有调整,直接对一个后缀\(+\)上一些数,直接看有没有即可
注意\(1e12\)的限制
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=2e5+5;
int n;
int a[MAXN];
long long b[MAXN];
int Sur[MAXN];
signed main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&n);
if(n==1)
{
printf("Yes\n0");
return 0;
}
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
if(a[i]==-1)
{
a[i]=0;
}
}
if(a[n]==1)
{
for(int i=1;i<=n;i++)
{
a[i]^=1;
}
}
for(int i=n;i>=1;i--)
{
Sur[i]=Sur[i+1]+(a[i]==1);
}
b[0]=-1e6;
long long D0=0,D1=0;
int f=0;
for(int i=1;i<=n;i++)
{
if(a[i]==1)
{
if((Sur[i]>(n-i+1)-Sur[i])&&(!f))
{
f=i;
b[i]=b[i-1]+1;
}
else
{
b[i]=b[i-1]+1;
}
D1+=b[i];
}
else if(a[i]==0)
{
b[i]=b[i-1]+1;
D0+=b[i];
}
}
if(f&&(D0>D1))
{
long long Det=(D0-D1)/(Sur[f]-((n-f+1)-Sur[f]));
for(int i=f;i<=n;i++)
{
b[i]+=Det+1;
if(a[i]==0)
{
D0+=(Det+1);
}
else
{
D1+=(Det+1);
}
}
//printf("fuck\n");
}
//printf("%lld %lld\n",D0,D1);
if(D0>D1&&(!f))
{
printf("No");
}
else
{
long long det=D1-D0;
b[n]+=det;
printf("Yes\n");
for(int i=1;i<=n;i++)
{
printf("%lld ",b[i]);
}
}
}
D
考虑每个\(x\)在第\(i\)位的贡献
可以发现第\(i-1\)位的影响就是它是否进位
如果设\(dp_{i,j}\)为前\(i\)位有\(j\)个进位
然后\(j\)个进位的数是固定的,我们可以直接枚举填的数即可
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=2e5+5;
int n;
int a[MAXN];
int dp[11][MAXN];
int C[11];
vector<pair<int,int> >V;
signed main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&n);
int Sum=0;
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
int Now=a[i];
for(int j=1;j<=9;j++)
{
Sum+=(Now%10);
Now/=10;
}
}
memset(dp,0x3f,sizeof(dp));
dp[0][0]=0;
int Mul=1;
for(int ie=1;ie<=9;ie++)
{
for(int j=0;j<=10;j++)
{
C[j]=0;
}
for(int i=1;i<=n;i++)
{
C[(a[i]/Mul)%10]++;
}
V.clear();
for(int i=1;i<=n;i++)
{
V.push_back((make_pair(-(a[i]%Mul),i)));
}
sort(V.begin(),V.end());
for(int i=0;i<=n;i++)
{
if(dp[ie-1][i]!=0x3f3f3f3f)
{
// if(ie==2)
// {
// printf("%d %d----\n",i,C[8]);
// }
for(int j=0;j<=9;j++)
{
int Nr=(j*n);
int Cp=0;
for(int k=0;k<=10;k++)
{
if(j+k>=10)
{
Cp+=C[k];
}
}
Nr=(Nr-9*Cp);
//printf("%d----\n",Nr);
dp[ie][Cp]=min(dp[ie][Cp],dp[ie-1][i]+Nr);
}
}
if(i!=n)
{
int p=V[i].second;
//printf("%d??\n",p);
C[(a[p]/Mul)%10]--;
C[(a[p]/Mul)%10+1]++;
}
}
// for(int i=0;i<=n;i++)
// {
// printf("%d %d %d:::\n",ie,i,dp[ie][i]);
// }
Mul*=10;
}
int Res=0x3f3f3f3f;
for(int i=0;i<=n;i++)
{
Res=min(Res,dp[9][i]);
}
printf("%d\n",Res+Sum);
}
E
注意\(f(X)\)是最小的
如果我们知道了\([L,R]\),然后\(X\)后面那位一定是要填在\(L-1\)或者\(R+1\)
如果填的是\(L-1\),必须满足\((Y_{L-1}\le Y_L)\)
如果填的是\(R+1\),必须满足\(Y_R>Y_L\)(防止重复)
这个区间\(dp\)直接做是\(O(n^2)\)的
不过可以注意到很多状态是用不到的
可以发现如果要转移到\(1\),说明\([1,L]\)必须是个不降的序列
而且\(i\)向右转移的范围是最大的\(R\)使得\([i,R]\)最小的数大于\(i\)
然后可以发现这玩意长得像若干个阶梯状的转移,阶级间的转移是个卷积的形式
Show Code
#include<bits/stdc++.h>
#define eps 1e-9
using namespace std;
const int MAXN=6e5+5;
const int MOD=998244353;
const int g=3;
int Pow(int a,int b,int p)
{
int res=1;
int base=a;
while(b)
{
if(b&1)
{
res=((long long)res*base)%p;
}
base=((long long)base*base)%p;
b>>=1;
}
return res;
}
int inv(int a,int p)
{
return Pow(a,p-2,p);
}
int Rev[MAXN*4];
int inv_fac[MAXN];
int fac[MAXN];
int C(int n,int m)
{
if(n<m||m<0)
{
return 0;
}
if(n==m||m==0)
{
return 1;
}
return ((((long long)fac[n]*inv_fac[m])%MOD)*inv_fac[n-m])%MOD;
}
struct Poly{
vector<int>U;
void NTT(int Limit,int type)
{
int Len=(1<<Limit);
for(int i=0;i<Len;i++)
{
Rev[i]=((Rev[i>>1]>>1)|((i&1)<<(Limit-1)));
}
while(U.size()<Len)
{
U.push_back(0);
}
for(int i=0;i<Len;i++)
{
if(i<Rev[i])
{
swap(U[i],U[Rev[i]]);
}
}
for(int l=1;l<Len;l<<=1)
{
int Wn=Pow(g,(MOD-1)/(l<<1),MOD);
if(type==-1)
{
Wn=inv(Wn,MOD);
}
for(int i=0;i<Len;i+=(l<<1))
{
int W=1;
for(int j=i;j<i+l;j++,W=((long long)W*Wn)%MOD)
{
int Xc=U[j];
int Yc=((long long)U[j+l]*W)%MOD;
U[j]=((long long)Xc+Yc)%MOD;
U[j+l]=((long long)Xc-Yc+MOD)%MOD;
}
}
}
if(type==-1)
{
int Liv=inv(Len,MOD);
for(int i=0;i<Len;i++)
{
U[i]=((long long)U[i]*Liv)%MOD;
}
}
}
};
Poly Mul_NTT(Poly A,Poly B)
{
int N=A.U.size();
int M=B.U.size();
int nox=1;
int Lm=0;
while(nox<=(N+M-2))
{
nox<<=1;
Lm++;
}
A.NTT(Lm,1);
B.NTT(Lm,1);
for(int i=0;i<nox;i++)
{
A.U[i]=((long long)A.U[i]*B.U[i])%MOD;
}
A.NTT(Lm,-1);
while(A.U.size()>(N+M-1))
{
A.U.pop_back();
}
return A;
}
char s[MAXN];
Poly A;
struct Sery{
int l,r,R;
}a[MAXN];
int dp[MAXN][25];
int Lg[MAXN];
int Query(int l,int r)
{
if(l>r)
{
return 0x3f3f3f3f;
}
int k=Lg[r-l+1];
return min(dp[l][k],dp[r-(1<<k)+1][k]);
}
signed main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
fac[0]=1;
for(int i=1;i<=MAXN-5;i++)
{
fac[i]=((long long)fac[i-1]*i)%MOD;
}
inv_fac[MAXN-5]=inv(fac[MAXN-5],MOD);
for(int i=MAXN-5-1;i>=1;i--)
{
inv_fac[i]=((long long)inv_fac[i+1]*(i+1))%MOD;
}
scanf("%s",s+1);
int n=strlen(s+1);
for(int i=1;i<=n;i++)
{
dp[i][0]=s[i];
Lg[i]=log2(i);
}
for(int j=1;(1<<j)<=n;j++)
{
for(int i=1;i+(1<<j)-1<=n;i++)
{
dp[i][j]=min(dp[i][j-1],dp[i+(1<<j-1)][j-1]);
}
}
A.U.resize(n+1,0);
int Pi=1;
int Cnt=0;
while(Pi<=n)
{
++Cnt;
a[Cnt].l=Pi;
while((Pi+1<=n)&&(s[Pi]==s[Pi+1]))
{
++Pi;
}
a[Cnt].r=Pi;
int l=Pi;
int r=n;
int Key=Pi;
while(l<=r)
{
int mid=(l+r)>>1;
if(Query(Pi+1,mid)>s[Pi])
{
l=mid+1;
Key=mid;
}
else
{
r=mid-1;
}
}
a[Cnt].R=Key;
if((Pi<=n)&&(s[Pi+1]>s[Pi]))
{
++Pi;
}
else
{
break;
}
}
// printf("%d\n",Cnt);
// for(int i=1;i<=Cnt;i++)
// {
// printf("%d %d %d\n",a[i].l,a[i].r,a[i].R);
// }
Poly B;
B.U.resize(n+1,0);
for(int i=Cnt;i>=1;i--)
{
int Len=a[i].r-a[i].l+1;
for(int j=0;j<=n;j++)
{
B.U[j]=C(j+Len-1,Len-1);
}
A.U[a[i].r]=1;
A=Mul_NTT(A,B);
for(int j=0;j<=n;j++)
{
if(j>=a[i].l&&j<=a[i].R)
{
}
else
{
A.U[j]=0;
}
}
for(int j=a[i].l;j<a[i].r;j++)
{
A.U[j]=1;
}
// printf("%d::\n",i);
// for(int j=0;j<=n;j++)
// {
// printf("%d ",A.U[j]);
// }
// printf("\n");
// for(int j=0;j<=n;j++)
// {
// printf("%d ",B.U[j]);
// }
// printf("\n");
}
printf("%d\n",A.U[n]);
}
F
首先考虑由总方案减去不合法的
我们考虑先减去哪些颜色个数都不对的,这个是个简单容斥,总和为\(3^m-(2^m\times3)+3\)
然后再考虑减去哪些用了三个颜色但依旧没有形成三颜色路径的方案
可以发现对于一个环,如果环的大小\(\ge4\),那这个环的颜色均是相同的,因为如果不同,对于多出来的边一定可以在外面找到一些边形成三颜色路径,注意满足条件是\(n>4\),所以这里我们就把\(n\le4\)的特殊处理一下
然后进一步考虑,发现如果都是同色环的话实际上由一个割点分出的若干个点双均需满足同色,因为不能形成三个异色路径,而用割点来恰好能划分所有方案
而对于环大小\(=3\)的,我们发现如果与它相连的边只有一条且这条边与它相对的边颜色相同时满足条件,则一个满足条件的三元环对答案的贡献为\(3!\)
这两种情况均可用园方树统计
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MOD=998244353;
const int MAXN=4e5+5;
int Pow(int a,int b,int p)
{
int res=1;
int base=a;
while(b)
{
if(b&1)
{
res=((long long)res*base)%p;
}
base=((long long)base*base)%p;
b>>=1;
}
return res;
}
int Cal(int x)
{
if(x<3)
{
return 0;
}
return ((long long)Pow(3,x,MOD)+3-(3ll*Pow(2,x,MOD))%MOD+MOD)%MOD;
}
int n,m;
int x,y;
vector<int>g[MAXN];
int dfn[MAXN];
int low[MAXN];
int cnt_dfn;
int cnt_node;
stack<int>st;
vector<int>G[MAXN];
void dfs(int x,int f)
{
dfn[x]=++cnt_dfn;
low[x]=dfn[x];
st.push(x);
for(int i=0;i<g[x].size();i++)
{
int v=g[x][i];
if(v==f)
{
continue;
}
if(dfn[v])
{
low[x]=min(low[x],dfn[v]);
}
else
{
dfs(v,x);
low[x]=min(low[x],low[v]);
if(low[v]>=dfn[x])
{
++cnt_node;
while(st.size())
{
G[cnt_node].push_back(st.top());
G[st.top()].push_back(cnt_node);
if(st.top()==v)
{
st.pop();
break;
}
st.pop();
}
G[cnt_node].push_back(x);
G[x].push_back(cnt_node);
}
}
}
}
void find(int x)
{
}
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d %d",&n,&m);
int Px,Py;
for(int i=1;i<=m;i++)
{
scanf("%d %d",&x,&y);
g[x].push_back(y);
g[y].push_back(x);
Px=x;
Py=y;
}
if(n==3)
{
printf("0");
return 0;
}
else if(n==4)
{
if(m==6&&Px==3&&Py==4)
{
printf("534");
return 0;
}
else if(m==5&&Px==1&&Py==2)
{
printf("144");
return 0;
}
}
cnt_node=n;
dfs(1,0);
int Res=Cal(m);
for(int i=1;i<=n;i++)
{
Res=((long long)Res-Cal(G[i].size())+MOD)%MOD;
}
for(int i=n+1;i<=cnt_node;i++)
{
if(G[i].size()==3)
{
int f1=0;
for(int j=0;j<G[i].size();j++)
{
int v=G[i][j];
if(G[v].size()>=2)
{
f1++;
}
}
if(f1<=1)
{
Res=((long long)Res-6+MOD)%MOD;
}
}
}
printf("%d\n",Res);
}
ARC156
A
简单分类讨论
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=2e5+5;
char s[MAXN];
int T;
int n;
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&T);
while(T--)
{
scanf("%d",&n);
scanf("%s",s+1);
int Cnt=0;
for(int i=1;i<=n;i++)
{
if(s[i]=='1')
{
++Cnt;
}
}
if(Cnt&1)
{
printf("-1\n");
}
else
{
if(Cnt==2)
{
int f=0;
for(int i=1;i<n;i++)
{
if(s[i]=='1'&&s[i+1]=='1')
{
f=i;
}
}
if(f)
{
if(n==3||n==2)
{
printf("-1\n");
}
else if(n==4)
{
if(f==2)
{
printf("3\n");
}
else
{
printf("2\n");
}
}
else
{
printf("2\n");
}
}
else
{
printf("1\n");
}
}
else
{
printf("%d\n",Cnt/2);
}
}
}
}
B
考虑枚举我填的数最\(i\)是多少,然后用剩下的次数填到小于\(i\)的数
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=4e5+5;
const int MOD=998244353;
int n,k;
int a[MAXN];
int fac[MAXN];
int Pow(int a,int b,int p)
{
int res=1;
int base=a;
while(b)
{
if(b&1)
{
res=((long long)res*base)%p;
}
base=((long long)base*base)%p;
b>>=1;
}
return res;
}
int inv_fac[MAXN];
int inv(int a,int p)
{
return Pow(a,p-2,p);
}
int C(int n,int m)
{
if(m<0||n<m)
{
return 0;
}
if(m==0||n==m)
{
return 1;
}
return ((((long long)fac[n]*inv_fac[m])%MOD)*(inv_fac[n-m]))%MOD;
}
int Vis[MAXN];
int main()
{
fac[0]=1;
for(int i=1;i<=MAXN-5;i++)
{
fac[i]=((long long)fac[i-1]*i)%MOD;
}
inv_fac[MAXN-5]=inv(fac[MAXN-5],MOD);
for(int i=MAXN-5-1;i>=0;i--)
{
inv_fac[i]=((long long)inv_fac[i+1]*(i+1))%MOD;
}
scanf("%d %d",&n,&k);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
Vis[a[i]]=1;
}
int Res=0;
for(int i=0;i<=MAXN-5;i++)
{
// printf("%d %d?\n",i,=);
if(Vis[i])
{
continue;
}
// printf("%d?\n",i);
if(k)
{
Res=((long long)Res+(C(i-1+k,k)))%MOD;
// printf("%d %d?\n",i-1+k,k);
k--;
}
else
{
Res++;
break;
}
}
printf("%d",Res);
}
C
智慧题😂
大胆猜想答案是\(1\)
具体构造是每次选叶子然后交换\(P_i,P_j\)之后删去
证明的话考虑我们实际上就是想让\((i,P_i)\)是交叉的,而这样构造后一条链的\((i,j)\)前面的肯定不会产生贡献,而后面的因为交错了也不会有贡献
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=1e5+5;
int n;
int x,y;
int Rd[MAXN];
vector<int>g[MAXN];
int P[MAXN];
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<n;i++)
{
scanf("%d %d",&x,&y);
g[x].push_back(y);
g[y].push_back(x);
Rd[x]++;
Rd[y]++;
}
queue<int>q;
for(int i=1;i<=n;i++)
{
P[i]=i;
if(Rd[i]==1)
{
q.push(i);
}
}
while(q.size()>=2)
{
int t1=q.front();
q.pop();
int t2=q.front();
q.pop();
swap(P[t1],P[t2]);
for(int i=0;i<g[t1].size();i++)
{
int v=g[t1][i];
Rd[v]--;
if(Rd[v]==1)
{
q.push(v);
}
}
for(int i=0;i<g[t2].size();i++)
{
int v=g[t2][i];
Rd[v]--;
if(Rd[v]==1)
{
q.push(v);
}
}
}
for(int i=1;i<=n;i++)
{
printf("%d ",P[i]);
}
}
D
首先我们构造函数\(F(x)=(\sum x^{A_i})\),我们要求的就是\(F^k(x)\)中奇数次项的异或和
注意到\(F^2(x)=(\sum x^{2A_i})\)(对系数\(\bmod 2\))
可以发现\(2\)的次幂的次数相当于是对每个\(A_i\times2^k\)
如果我们对\(k\)二进制拆分,于是我们可以将次数缩减为\(log\)级别
然后考虑对这些物品\(dp\),设\(dp_{i,x}\)为前\(i\)位,\(sum\bmod 2^{i}=x\)的方案数\(\bmod 2\)
注意到这样不会影响到前面的位置,所以我们只用计算前一个二进制位哪些\(x\)能被算贡献即可
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=2005;
int n;
long long k;
int a[MAXN];
int dp[MAXN];
int Tmp[MAXN];
int Rtm[MAXN];
int main()
{
scanf("%d %lld",&n,&k);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
}
int Cnt=0;
int last=0;
long long Res=0;
dp[0]=1;
while(k)
{
if(k&1ll)
{
long long Po=(1<<(Cnt-last));
for(int i=0;i<=MAXN-5;i++)
{
Tmp[i]=dp[i];
dp[i]=0;
Rtm[i]=0;
}
for(int i=0;i<=MAXN-5;i++)
{
if(Tmp[i])
{
for(int j=1;j<=n;j++)
{
Rtm[i%Po]^=1;
dp[(i/Po)+a[j]]^=1;
}
}
}
int Rp=0;
for(int i=0;i<=MAXN-5;i++)
{
if(Rtm[i])
{
Rp^=i;
}
}
Res=(Res+(1ll<<last)*Rp);
last=Cnt;
}
k>>=1ll;
Cnt++;
}
int Rp=0;
for(int i=0;i<=MAXN-5;i++)
{
if(dp[i])
{
Rp^=i;
}
}
Res=(Res+(1ll<<last)*Rp);
printf("%lld\n",Res);
}
E
太难了/kk
ARC158
A
\(ARC159C\)的超级弱化版??
每次操作相当于一个\(+2\)一个\(-2\)
Show Code
#include<bits/stdc++.h>
using namespace std;
long long Abs(long long x)
{
return x>0?x:-x;
}
int T;
long long a,b,c;
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&T);
while(T--)
{
scanf("%lld %lld %lld",&a,&b,&c);
long long Sum=(a+b+c);
if(Sum%3)
{
printf("-1\n");
continue;
}
else
{
long long g=Sum/3;
long long Na=0;
if(Abs(a-g)&1)
{
printf("-1\n");
continue;
}
else
{
Na=max(Na,Abs(a-g)/2);
}
if(Abs(b-g)&1)
{
printf("-1\n");
continue;
}
else
{
Na=max(Na,Abs(b-g)/2);
}
if(Abs(c-g)&1)
{
printf("-1\n");
continue;
}
else
{
Na=max(Na,Abs(c-g)/2);
}
printf("%lld\n",Na);
}
}
}
B
\(\dfrac{x+y+z}{xyz}=\dfrac{1}{xy}+\dfrac{1}{xz}+\dfrac{1}{yz}\)
不难发现取三个\(\dfrac{1}{x}\)最大/最小的数即可
有负数的话直接把前面\(3\)个和后面\(3\)个拉出了暴力即可
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=2e5+5;
int n;
int a[MAXN];
double v[MAXN];
double V[16];
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
v[i]=(1.0/a[i]);
}
sort(v+1,v+1+n);
int Cnt=0;
for(int i=1;i<=3;i++)
{
V[++Cnt]=v[i];
}
for(int i=n-2;i<=n;i++)
{
if(i>3)
{
V[++Cnt]=v[i];
}
}
double Maxi=-1e15;
double Mini=1e15;
for(int i=1;i<=Cnt;i++)
{
for(int j=i+1;j<=Cnt;j++)
{
for(int k=j+1;k<=Cnt;k++)
{
double R=((V[i]*V[j]+V[j]*V[k]+V[i]*V[k]));
Maxi=max(Maxi,R);
Mini=min(Mini,R);
}
}
}
printf("%.15lf\n",Mini);
printf("%.15lf\n",Maxi);
}
C
考虑对\(f(X)\)求和然后减去进位的次数\(\times9\)
然后枚举在哪进的位\(i\),对于\(a,b\),只要\(a\bmod 10^i+b\bmod 10^i>10^i\)则会进位,这里直接双指针扫一下或者二分即可
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=2e5+5;
int n;
long long A[MAXN];
long long B[MAXN];
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&n);
long long Res=0;
for(int i=1;i<=n;i++)
{
scanf("%lld",&A[i]);
long long Mul=1;
for(int j=1;j<=15;j++)
{
Res+=((A[i]/Mul)%10)*n*2;
Mul*=10;
}
}
long long Mul=1;
for(int s=1;s<=15;s++)
{
Mul*=10;
for(int i=1;i<=n;i++)
{
B[i]=(A[i]%Mul);
}
sort(B+1,B+1+n);
for(int i=1;i<=n;i++)
{
long long Rest=(Mul-B[i]);
int l=1;
int r=n;
int Key=-1;
while(l<=r)
{
int mid=(l+r)>>1;
if(B[mid]>=Rest)
{
Key=mid;
r=mid-1;
}
else
{
l=mid+1;
}
}
if(Key!=-1)
{
Res-=(9ll*(n-Key+1));
}
}
}
printf("%lld\n",Res);
}
D
抽象题
注意到等式左边比右边次数大一,把分别设为\(F(x,y,z),G(x,y,z)\)
我们对于任意的\(x,y,z\),如果存在\(t\)满足\(F(x,y,z)=G(x,y,z)t\bmod p\)
则\(F(\frac{x}{t},\frac{y}{t},\frac{z}{t})=G(\frac{x}{t},\frac{y}{t},\frac{z}{t})\)
然后我们就可以随机一组\((x,y,z)\)只要\(F,G\)均不为\(0\)即可
Show Code
#include<bits/stdc++.h>
#define int long long
using namespace std;
int Pow(int a,int b,int p)
{
int res=1;
int base=a;
while(b)
{
if(b&1)
{
res=((long long)res*base)%p;
}
base=((long long)base*base)%p;
b>>=1;
}
return res;
}
int inv(int a,int p)
{
return Pow(a,p-2,p);
}
int T;
int n;
int p;
int F(int x,int y,int z)
{
int t1=((long long)x+y+z)%p;
int t2=((long long)Pow(x,n,p)+Pow(y,n,p)+Pow(z,n,p))%p;
int t3=((long long)Pow(x,2*n,p)+Pow(y,2*n,p)+Pow(z,2*n,p))%p;
t1=((long long)t1*t2)%p;
t1=((long long)t1*t3)%p;
return t1;
}
int G(int x,int y,int z)
{
return ((long long)Pow(x,3*n,p)+Pow(y,3*n,p)+Pow(z,3*n,p))%p;
}
mt19937 NIU(time(0));
signed main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%lld",&T);
while(T--)
{
scanf("%lld %lld",&n,&p);
while(1)
{
int x=((rand())%(p-1))+1;
int y=((rand())%(p-1))+1;
int z=((rand())%(p-1))+1;
int f=F(x,y,z);
int g=G(x,y,z);
if(x==y||y==z||x==z)
{
continue;
}
if(f&&g)
{
int t=((long long)g*inv(f,p))%p;
int X=((long long)x*t)%p;
int Y=((long long)y*t)%p;
int Z=((long long)z*t)%p;
if(Z<Y)
{
swap(Z,Y);
}
if(Y<X)
{
swap(X,Y);
}
if(Z<Y)
{
swap(Z,Y);
}
printf("%lld %lld %lld\n",X,Y,Z);
break;
}
}
}
}
E
想到分治就好做了(虽然我一直在\(dp\)的方向想
对于\([L,R]\)计算跨越\(mid\)的贡献
考虑路径由\((mid,0),(mid+1,0)\)或\((mid,1),(mid+1,1)\)拼接起来,我们可以直接计算每个点到这四个点的最短距离,然后分类讨论一下他的路径是由哪个点拼接起来的就行了
Show Code
// LUOGU_RID: 122332688
#include<bits/stdc++.h>
using namespace std;
const int MOD=998244353;
const int MAXN=4e5+5;
int n;
int a[MAXN][2];
int Res=0;
long long A[MAXN][2];
long long B[MAXN][2];
vector<pair<long long,pair<int,int> > >V1,V2;
int Sur[MAXN*2];
int Pre[MAXN*2];
void solve(int l,int r)
{
if(l==r)
{
Res=((long long)Res+(3ll*(a[l][0]+a[l][1]))%MOD)%MOD;
return;
}
int mid=(l+r)>>1;
solve(l,mid);
solve(mid+1,r);
for(int i=l;i<=r;i++)
{
A[i][0]=A[i][1]=B[i][0]=B[i][1]=1e15;
}
A[mid][0]=a[mid][0];
A[mid][1]=a[mid][0]+a[mid][1];
for(int i=mid-1;i>=l;i--)
{
long long t0=A[i+1][0]+a[i][0];
long long t1=A[i+1][1]+a[i][1];
A[i][0]=min(t0,t1+a[i][0]);
A[i][1]=min(t1,t0+a[i][1]);
}
B[mid][0]=a[mid][0]+a[mid][1];
B[mid][1]=a[mid][1];
for(int i=mid-1;i>=l;i--)
{
long long t0=B[i+1][0]+a[i][0];
long long t1=B[i+1][1]+a[i][1];
B[i][0]=min(t0,t1+a[i][0]);
B[i][1]=min(t1,t0+a[i][1]);
}
A[mid+1][0]=a[mid+1][0];
A[mid+1][1]=a[mid+1][0]+a[mid+1][1];
for(int i=mid+2;i<=r;i++)
{
long long t0=A[i-1][0]+a[i][0];
long long t1=A[i-1][1]+a[i][1];
A[i][0]=min(t0,t1+a[i][0]);
A[i][1]=min(t1,t0+a[i][1]);
}
B[mid+1][0]=a[mid+1][0]+a[mid+1][1];
B[mid+1][1]=a[mid+1][1];
for(int i=mid+2;i<=r;i++)
{
long long t0=B[i-1][0]+a[i][0];
long long t1=B[i-1][1]+a[i][1];
B[i][0]=min(t0,t1+a[i][0]);
B[i][1]=min(t1,t0+a[i][1]);
}
V1.clear();
V2.clear();
for(int i=l;i<=mid;i++)
{
V1.push_back(make_pair(A[i][0]-B[i][0],make_pair(i,0)));
V1.push_back(make_pair(A[i][1]-B[i][1],make_pair(i,1)));
}
for(int i=mid+1;i<=r;i++)
{
V2.push_back(make_pair(B[i][0]-A[i][0],make_pair(i,0)));
V2.push_back(make_pair(B[i][1]-A[i][1],make_pair(i,1)));
}
sort(V1.begin(),V1.end());
sort(V2.begin(),V2.end());
int Pi=0;
Pre[0]=(B[V2[0].second.first][V2[0].second.second])%MOD;
for(int i=1;i<V2.size();i++)
{
Pre[i]=((long long)Pre[i-1]+(B[V2[i].second.first][V2[i].second.second]%MOD))%MOD;
}
Sur[V2.size()]=0;
for(int i=V2.size()-1;i>=0;i--)
{
Sur[i]=((long long)Sur[i+1]+(A[V2[i].second.first][V2[i].second.second]%MOD))%MOD;
}
for(int i=0;i<V1.size();i++)
{
while((Pi<V2.size())&&(V2[Pi].first<V1[i].first))
{
++Pi;
}
int To=0;
To=((long long)To+(Sur[Pi]))%MOD;
To=((long long)To+(((long long)A[V1[i].second.first][V1[i].second.second]%MOD)*(V2.size()-Pi))%MOD)%MOD;
if(Pi)
{
To=((long long)To+(Pre[Pi-1]))%MOD;
To=((long long)To+(((long long)B[V1[i].second.first][V1[i].second.second]%MOD)*(Pi))%MOD)%MOD;
}
Res=((long long)Res+(2ll*To)%MOD)%MOD;
//printf("%d %d %d %d??\n",V1[i].second.first,V1[i].second.second,To,Pi);
}
}
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&n);
for(int i=0;i<=1;i++)
{
for(int j=1;j<=n;j++)
{
scanf("%d",&a[j][i]);
}
}
solve(1,n);
printf("%d\n",Res);
}
ARC159
A
不知道复制\(k\)遍有什么用,其实都是一样的
Show Code
#include<bits/stdc++.h>
using namespace std;
int n,m;
int a[105][105];
int q;
long long s,t;
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d %d",&n,&m);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
scanf("%d",&a[i][j]);
if(a[i][j]==0)
{
a[i][j]=0x3f3f3f3f;
}
}
}
for(int k=1;k<=n;k++)
{
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
a[i][j]=min(a[i][j],a[i][k]+a[k][j]);
}
}
}
scanf("%d",&q);
while(q--)
{
scanf("%lld %lld",&s,&t);
s=((s-1)%n)+1;
t=((t-1)%n)+1;
if(a[s][t]==0x3f3f3f3f)
{
printf("-1\n");
}
else
{
printf("%d\n",a[s][t]);
}
}
}
B
被诈骗了/kk
直觉上直接暴力,但\(T\)了很多点
分析一下,这个\(g\)一定是递增的,因为\(A-B\)不变,因此上一个的\(g=\gcd(A-B,B)\)是一定能保留的
\(C=A-B\)
考虑什么时候\(g\)增大,具体的就是\(dg|B-kg,dg|C\)
这玩意直接枚举\(C\)的因数
由于每次\(g\)至少增大到\(2g\),所以最多\(log\)次
Show Code
#include<bits/stdc++.h>
using namespace std;
long long A,B;
long long gcd(long long a,long long b)
{
if(b==0)
{
return a;
}
return gcd(b,a%b);
}
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%lld %lld",&A,&B);
long long Tot=0;
if(A>B)
{
swap(A,B);
}
long long C=B-A;
while((A>=1)&&(B>=1))
{
long long g=gcd(C,B);
long long k=0x3f3f3f3f;
if(B%A==0)
{
Tot++;
//printf("%lld %lld???\n",A,B);
break;
}
for(long long i=1;i*i<=(C/g);i++)
{
if((C/g)%i==0)
{
long long d=i;
long long Rb=(A/g);
if(Rb>d)
{
k=min(k,(Rb%d)?(Rb%d):Rb);
}
d=(C/g)/i;
Rb=(A/g);
if(Rb>d)
{
k=min(k,(Rb%d)?(Rb%d):Rb);
}
}
}
Tot+=k;
A-=k*g;
B-=k*g;
//printf("%lld %lld\n",A,B);
}
printf("%lld\n",Tot);
}
C
又被诈骗了/kk
首先考虑总和一定要为\(n\)的倍数或\(n/2\)的倍数,看\(n\)是不是偶数
如果\(n\)是偶数就随便操作一次让他全部是\(n\)的倍数
设\(g=\dfrac{Sum}{n}\),每次我们选\(a_i<g,a_j>g\)的\((i,j)\),并分别操作\((1,n-1),(2,n)\),这样两者的差减\(2\),给其他数操作\((p,n-p+1)\),相当于整体\(+(n+1)\)但\(i,j\)分别\(+1,-1\)
可以发现这样一定有解
Show Code
#include<bits/stdc++.h>
using namespace std;
int n;
int a[55];
vector<vector<int> >Ans;
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&n);
int Sum=0;
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
Sum+=a[i];
}
if((n&1)&&(Sum%n))
{
printf("No");
return 0;
}
if((n%2==0)&&((Sum%(n/2))))
{
printf("No");
return 0;
}
if((n%2==0)&&(Sum%n))
{
vector<int>Tmp;
for(int i=1;i<=n;i++)
{
Sum+=i;
a[i]+=i;
Tmp.push_back(i);
}
Ans.push_back(Tmp);
}
int g=(Sum)/n;
while(1)
{
int pi=-1,pj=-1;
for(int i=1;i<=n;i++)
{
if(a[i]<g)
{
pi=i;
break;
}
}
for(int i=1;i<=n;i++)
{
if(a[i]>g)
{
pj=i;
break;
}
}
if(pi==-1)
{
break;
}
int Now=3;
vector<int>t1,t2;
t1.clear();
t2.clear();
for(int i=1;i<=n;i++)
{
if(i==pi)
{
t2.push_back(n);
t1.push_back(2);
a[i]++;
}
else if(i==pj)
{
t2.push_back(n-1);
t1.push_back(1);
a[i]--;
}
else
{
t1.push_back(Now);
t2.push_back(n-Now+1);
++Now;
}
}
Ans.push_back(t1);
Ans.push_back(t2);
}
printf("Yes\n");
printf("%d\n",(int)Ans.size());
for(int i=0;i<Ans.size();i++)
{
for(int j=0;j<n;j++)
{
printf("%d ",Ans[i][j]);
}
printf("\n");
}
}
D
\(dp_i\)为前\(i\)个区间以\(r_i\)结尾的\(LIS\)
这玩意转移看一下区间有没有交即可
Show Code
#include<bits/stdc++.h>
#define ls Tree[p].lc
#define rs Tree[p].rc
using namespace std;
const int MAXN=2e5+5;
int n;
int l,r;
struct Seg_node{
int lc,rc;
int date;
};
struct Seg{
Seg_node Tree[MAXN*100];
int rt;
int cnt_node;
void Insert(int &p,int l,int r,int k,int x)
{
if(!p)
{
p=++cnt_node;
Tree[p].date=-0x3f3f3f3f;
Tree[p].lc=0;
Tree[p].rc=0;
}
Tree[p].date=max(Tree[p].date,x);
if(l==r)
{
return;
}
int mid=(l+r)>>1;
if(k<=mid)
{
Insert(ls,l,mid,k,x);
}
else
{
Insert(rs,mid+1,r,k,x);
}
}
int Query(int p,int l,int r,int ql,int qr)
{
if(!p)
{
return -0x3f3f3f3f;
}
if(l>=ql&&r<=qr)
{
return Tree[p].date;
}
int mid=(l+r)>>1;
int Res=-0x3f3f3f3f;
if(ql<=mid)
{
Res=max(Res,Query(ls,l,mid,ql,qr));
}
if(qr>mid)
{
Res=max(Res,Query(rs,mid+1,r,ql,qr));
}
return Res;
}
}t1,t2;
int dp[MAXN];
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&n);
dp[0]=0;
t1.Insert(t1.rt,0,1e9,0,0);
int Res=0;
for(int i=1;i<=n;i++)
{
scanf("%d %d",&l,&r);
dp[i]=t1.Query(t1.rt,0,1e9,0,l-1)+(r-l+1);
dp[i]=max(dp[i],t2.Query(t2.rt,0,1e9,l,r)+r);
t1.Insert(t1.rt,0,1e9,r,dp[i]);
t2.Insert(t2.rt,0,1e9,r,dp[i]-r);
Res=max(Res,dp[i]);
}
printf("%d\n",Res);
}
E
这玩意就是建一颗二叉搜索树,树高是\(log\)级别的
考虑\((i,i+1)\)一定有祖先关系,因为如果存在\(lca\not=i,i+1\),一定有\(i<lca<i+1\)
然后统计答案的话就是\([c,d]\)和\(1\)虚树上的点\(\times2\)减去\(c,d\)的深度和,虚树经典结论
然后\([c,d]\)和\(1\)虚树上的点统计类似与线段树,把路径上的点全部加上即可
Show Code
// LUOGU_RID: 122153078
#include<bits/stdc++.h>
using namespace std;
long long n;
int m;
int q;
int a[105];
int b[105];
long long c,d;
int Get_dep(long long l,long long r,long long p,int dep)
{
if(l==r)
{
return dep;
}
long long mid=((l*a[dep%m]+r*b[dep%m])/(a[dep%m]+b[dep%m]));
if(p==mid)
{
return dep;
}
if(p<mid)
{
return Get_dep(l,mid-1,p,dep+1);
}
else
{
return Get_dep(mid+1,r,p,dep+1);
}
}
long long Get(long long l,long long r,long long ql,long long qr,int dep)
{
if(l>r)
{
return 0;
}
if(r<ql||l>qr)
{
return 0;
}
if(l>=ql&&r<=qr)
{
return (r-l+1);
}
long long mid=((l*a[dep%m]+r*b[dep%m])/(a[dep%m]+b[dep%m]));
long long Res=1;
Res+=Get(l,mid-1,ql,qr,dep+1);
Res+=Get(mid+1,r,ql,qr,dep+1);///
return Res;
}
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%lld %d",&n,&m);
for(int i=0;i<m;i++)
{
scanf("%d %d",&a[i],&b[i]);
}
scanf("%d",&q);
while(q--)
{
scanf("%lld %lld",&c,&d);
printf("%lld\n",2*(Get(1,n,c,d,0)-1)-Get_dep(1,n,c,0)-Get_dep(1,n,d,0));
}
}
ARC161
A
排序后直接奇偶分类地填即可
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=2e5+5;
int n;
int a[MAXN];
int b[MAXN];
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
}
sort(a+1,a+1+n);
int Pi=1;
for(int i=1;i<=n;i+=2)
{
b[i]=a[Pi++];
}
for(int i=2;i<=n;i+=2)
{
b[i]=a[Pi++];
}
bool f=1;
for(int i=1;i<=n;i++)
{
if(i%2==0)
{
if(b[i]>b[i-1]&&b[i]>b[i+1])
{
}
else
{
//printf("%d???\n",i);
f=0;
}
}
}
if(f)
{
printf("Yes\n");
}
else
{
printf("No");
}
}
B
直接看\(n\)的二进制里有多少个\(1\),如果有\(3\)个以上就直接取最高的三位即可,否则我们就看\(n\)最近的二进制位,让他降位即可
Show Code
#include<bits/stdc++.h>
using namespace std;
int T;
long long n;
int b[1005];
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&T);
while(T--)
{
scanf("%lld",&n);
int Cnt=0;
long long Now=n;
while(Now)
{
b[Cnt++]=(Now&1ll);
Now>>=1ll;
}
int Lp=0;
for(int i=0;i<Cnt;i++)
{
if(b[i])
{
Lp++;
}
}
cerr<<Lp<<endl;
if(Lp>=3)
{
long long Ne=n;
for(int i=0;i<Cnt;i++)
{
if(b[i]&&Lp>3)
{
Ne-=(1ll<<(i));
Lp--;
}
}
printf("%lld\n",Ne);
}
else
{
long long Ne=0;
if(Cnt>=4)
{
if(Lp==1)
{
for(int i=Cnt-2;i>=Cnt-4;i--)
{
Ne+=(1ll<<(i));
}
printf("%lld\n",Ne);
}
else
{
if((b[0])||(b[1]))
{
for(int i=Cnt-2;i>=Cnt-4;i--)
{
Ne+=(1ll<<(i));
}
printf("%lld\n",Ne);
}
else
{
Ne=n;
for(int i=2;i<Cnt;i++)
{
if(b[i])
{
Ne-=(1ll<<(i-2));
break;
}
}
printf("%lld\n",Ne);
}
}
}
else
{
printf("-1\n");
}
}
}
}
C
先选度数\(\ge3\)的作为根
考虑自低向上递推,我们记录当前\(x\)是否被确定为\(B,W\),以及满足条件时\(fa\)的要求即可
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=2e5+5;
int T;
int n;
int x,y;
vector<int>g[MAXN];
char s[MAXN];
int dp[MAXN];
int Rd[MAXN];
int Ned[MAXN];
bool found=1;
int Rt;
void dfs(int x,int f)
{
int Cnt1=0,Cnt2=0;
int Cnt0=0;
int Ned1=0;
int Ned2=0;
for(int i=0;i<g[x].size();i++)
{
int v=g[x][i];
if(v==f)
{
continue;
}
dfs(v,x);
if(Ned[v]==1)
{
Ned1++;
}
else if(Ned[v]==2)
{
Ned2++;
}
if(dp[v]==1)
{
Cnt1++;
}
else if(dp[v]==2)
{
Cnt2++;
}
else
{
Cnt0++;
}
}
if((Ned1)&&(Ned2))
{
found=0;
}
else if(Ned1)
{
dp[x]=1;
}
else if(Ned2)
{
dp[x]=2;
}
//printf("%d %d %d %d::\n",x,Cnt0,Cnt1,Cnt2);
if(s[x]=='B')
{
if((Cnt1+Cnt0>Cnt2+1)||(x==Rt&&(Cnt1+Cnt0>Cnt2)))
{
for(int i=0;i<g[x].size();i++)
{
int v=g[x][i];
if(v==f)
{
continue;
}
// printf("%d???\n",v);
if(dp[v]==0)
{
dp[v]=1;
// printf("%d???\n",v);
}
}
Ned[x]=0;
}
else if((Cnt1+Cnt0+1>Cnt2)&&(x!=Rt))
{
for(int i=0;i<g[x].size();i++)
{
int v=g[x][i];
if(v==f)
{
continue;
}
if(dp[v]==0)
{
dp[v]=1;
}
}
Ned[x]=1;
}
else
{
found=0;
}
}
else
{
if((Cnt2+Cnt0>Cnt1+1)||(x==Rt&&(Cnt2+Cnt0>Cnt1)))
{
for(int i=0;i<g[x].size();i++)
{
int v=g[x][i];
if(v==f)
{
continue;
}
if(dp[v]==0)
{
dp[v]=2;
}
}
Ned[x]=0;
}
else if((Cnt2+Cnt0+1>Cnt1)&&(x!=Rt))
{
for(int i=0;i<g[x].size();i++)
{
int v=g[x][i];
if(v==f)
{
continue;
}
if(dp[v]==0)
{
dp[v]=2;
}
}
Ned[x]=2;
}
else
{
//cerr<<"fuck"<<endl;
found=0;
}
}
}
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&T);
while(T--)
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
g[i].clear();
Rd[i]=0;
Ned[i]=0;
dp[i]=0;
}
for(int i=1;i<n;i++)
{
scanf("%d %d",&x,&y);
g[x].push_back(y);
g[y].push_back(x);
Rd[x]++;
Rd[y]++;
}
scanf("%s",s+1);
if(n==2)
{
printf("%c%c\n",s[2],s[1]);
continue;
}
found=1;
for(int i=1;i<=n;i++)
{
if(Rd[i]!=1)
{
Rt=i;
break;
}
}
dfs(Rt,0);
if(found)
{
for(int i=1;i<=n;i++)
{
if(dp[i]==1)
{
printf("B");
}
else
{
printf("W");
}
}
printf("\n");
}
else
{
printf("-1\n");
}
}
}
D
考虑直接构造一个图每个点的度数均为\(d\)
我是直接先取个环,然后再隔\(i\)个连边
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=1e5+5;
int n,d;
int D[MAXN];
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d %d",&n,&d);
d=(d*2);
if(d<=n-1)
{
printf("Yes\n");
for(int i=1;i<=n;i++)
{
D[i]=d;
}
for(int i=1;i<=n;i++)
{
for(int j=i+1;j<=i+(d/2);j++)
{
printf("%d %d\n",i,(j%n)?(j%n):n);
}
}
}
else
{
printf("No");
}
}
E
抽象题
直接随机一个颜色序列,貌似正确挺高的
然后直接\(2-SAT\)判就行了
Show Code
#include<bits/stdc++.h>
using namespace std;
mt19937 Niuzi(1e9+7);
const int MAXN=2e5+5;
int T;
int n,m;
int x,y;
int col[MAXN];
vector<int>g[MAXN];
int dfn[MAXN];
int low[MAXN];
int cnt_dfn;
int scc[MAXN];
int cnt_scc;
stack<int>st;
vector<int>G[MAXN];
void dfs(int x)
{
dfn[x]=++cnt_dfn;
low[x]=dfn[x];
st.push(x);
for(int i=0;i<G[x].size();i++)
{
int v=G[x][i];
if(dfn[v])
{
if(!scc[v])
{
low[x]=min(low[x],dfn[v]);
}
}
else
{
dfs(v);
low[x]=min(low[x],low[v]);
}
}
if(dfn[x]==low[x])
{
++cnt_scc;
while(st.size())
{
scc[st.top()]=cnt_scc;
if(st.top()==x)
{
st.pop();
break;
}
st.pop();
}
}
}
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&T);
while(T--)
{
scanf("%d",&n);
int m=3*n/2;
for(int i=1;i<=n;i++)
{
g[i].clear();
}
for(int i=1;i<=m;i++)
{
scanf("%d %d",&x,&y);
g[x].push_back(y);
g[y].push_back(x);
}
//cerr<<"fcuk"<<endl;
while(1)
{
for(int i=1;i<=n;i++)
{
col[i]=(Niuzi()%2);
}
for(int i=1;i<=2*n;i++)
{
dfn[i]=0;
low[i]=0;
scc[i]=0;
G[i].clear();
}
while(st.size())
{
st.pop();
}
cnt_dfn=0;
cnt_scc=0;
for(int i=1;i<=n;i++)
{
for(int j=0;j<g[i].size();j++)
{
for(int k=0;k<g[i].size();k++)
{
if(j==k)
{
continue;
}
G[g[i][j]+(col[i]^1)*n].push_back(g[i][k]+col[i]*n);
}
}
}
for(int i=1;i<=2*n;i++)
{
if(!dfn[i])
{
dfs(i);
}
}
// for(int i=1;i<=n;i++)
// {
// cerr<<col[i];
// }
// cerr<<endl;
bool found=0;
for(int i=1;i<=n;i++)
{
if(scc[i]==scc[i+n])
{
found=1;
}
}
if(found)
{
break;
}
}
//cerr<<"fkkf"<<endl;
for(int i=1;i<=n;i++)
{
if(col[i])
{
printf("B");
}
else
{
printf("W");
}
}
printf("\n");
}
}
ARC162
A
简单分类讨论即可
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=1e3+5;
int T;
int n;
int P[MAXN];
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&T);
while(T--)
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&P[i]);
}
int Res=0;
for(int i=1;i<=n;i++)
{
bool f=1;
for(int j=i+1;j<=n;j++)
{
if(P[j]<P[i])
{
f=0;
}
}
Res+=f;
}
printf("%d\n",Res);
}
}
B
一个初步的想法是将\(1-n\)每个数依次排好序,唯一可能出现的问题是目前想排的数被抵到末尾了,这里我们只需要把它调整\(n-1\)的位置即可,只有当剩余只有两个数出现这种情况时无解
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=1e3+5;
int n;
int P[MAXN];
int Tmp[MAXN];
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&P[i]);
}
vector<pair<int,int>>Opra;
for(int i=1;i<n;i++)
{
int Pos;
if(P[i]==i)
{
continue;
}
for(int j=i;j<=n;j++)
{
if(P[j]==i)
{
Pos=j;
break;
}
}
if(Pos==n)
{
if((n-i+1)<=2)
{
printf("No");
return 0;
}
Opra.push_back(make_pair(n-1,n-3));
Pos=n-1;
int gk=P[n-2];
P[n-2]=P[n-1];
P[n-1]=P[n];
P[n]=gk;
}
Opra.push_back(make_pair(Pos,i-1));
for(int j=i;j<=n;j++)
{
Tmp[j]=P[j];
}
P[i]=Tmp[Pos];
P[i+1]=Tmp[Pos+1];
int Poi=i;
for(int j=i+2;j<=n;j++)
{
if(Poi==Pos)
{
Poi+=2;
}
P[j]=Tmp[Poi];
++Poi;
}
}
printf("Yes\n");
printf("%ld\n",Opra.size());
for(int i=0;i<Opra.size();i++)
{
printf("%d %d\n",Opra[i].first,Opra[i].second);
}
}
C
很zz的博弈
很明显\(B\)只会填\(k\),填了\(u\)之后\(u\)的祖先都不可能赢
对于\(A\),她只能走第一步赢,因为\(B\)可以根据\(A\)选的点来破坏\(A\)想让\(u\)赢的意图
所以直接check一下\(A\)走一步能不能赢即可
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=1005;
int T;
int n,k;
int x;
int A[MAXN];
vector<int>g[MAXN];
int Vis[MAXN];
int Cnt=0;
void find(int x,int f)
{
if(A[x]!=-1)
{
Vis[A[x]]=1;
}
else
{
++Cnt;
}
for(int i=0;i<g[x].size();i++)
{
int v=g[x][i];
if(v==f)
{
continue;
}
find(v,x);
}
}
bool found=0;
void dfs(int x,int f)
{
for(int i=0;i<g[x].size();i++)
{
int v=g[x][i];
if(v==f)
{
continue;
}
dfs(v,x);
}
for(int i=0;i<=n;i++)
{
Vis[i]=0;
}
Cnt=0;
find(x,f);
int Mex;
for(int i=0;i<=n;i++)
{
if(!Vis[i])
{
Mex=i;
break;
}
}
if(Mex==k&&((!Cnt)||(Cnt==1)))
{
found=1;
}
if(Cnt==1)
{
//printf("%d???\n",Mex);
Vis[Mex]=1;
for(int i=0;i<=n;i++)
{
if(!Vis[i])
{
Mex=i;
break;
}
}
if(Mex==k)
{
//printf("%deee???\n",x);
found=1;
}
}
}
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&T);
while(T--)
{
scanf("%d %d",&n,&k);
for(int i=1;i<=n;i++)
{
g[i].clear();
}
for(int i=2;i<=n;i++)
{
scanf("%d",&x);
g[x].push_back(i);
}
for(int i=1;i<=n;i++)
{
scanf("%d",&A[i]);
}
found=0;
dfs(1,0);
if(found)
{
printf("Alice\n");
}
else
{
printf("Bob\n");
}
}
}
E
乍一看都不知道这个题在说些什么
仔细想想就可以发现设\(d_i\)为\(i\)出现的次数
我们要保证\(d_i\le A_i\)并且满足填入第\(i\)位的数\(j\)满足\(d_j\le A_i\)
这个\(d_i\le A_i\),经典\(dp\)
而对于后面的条件,我们可以按填的\(d_i\)从大到小\(dp\),这样就可以得到哪些位置能填以及哪些值能用
具体的设\(dp_{i,j,k}\)表示考虑了出现次数\(\ge i\)的,填了\(j\)种数,填了\(k\)个位置的方案数
转移直接枚举下一次填了\(t\)种数即可,时间复杂度因为\(j,i\le\dfrac{n}{i}\),精细实现是\(O(n^3)\)的,多个\(log\)好像会\(T\)
Show Code
// LUOGU_RID: 120706268
#include<bits/stdc++.h>
using namespace std;
const int MAXN=505;
const int MOD=998244353;
int n;
int a[MAXN];
int dp[MAXN][MAXN][MAXN];
int C[MAXN][MAXN];
int fac[MAXN];
int inv_fac[MAXN];
int Cp[MAXN];
int Pow(int a,int b,int p)
{
int res=1;
int base=a;
while(b)
{
if(b&1)
{
res=((long long)res*base)%p;
}
base=((long long)base*base)%p;
b>>=1;
}
return res;
}
int inv(int a,int p)
{
return Pow(a,p-2,p);
}
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
}
for(int i=0;i<=n;i++)
{
Cp[i]=0;
for(int j=1;j<=n;j++)
{
if(a[j]>=i)
{
Cp[i]++;
}
}
}
C[0][0]=1;
fac[0]=1;
for(int i=1;i<=n;i++)
{
C[i][0]=1;
fac[i]=((long long)fac[i-1]*i)%MOD;
for(int j=1;j<=n;j++)
{
C[i][j]=((long long)C[i-1][j]+C[i-1][j-1])%MOD;
}
}
inv_fac[n]=inv(fac[n],MOD);
for(int i=n-1;i>=0;i--)
{
inv_fac[i]=((long long)inv_fac[i+1]*(i+1))%MOD;
}
dp[n+1][0][0]=1;
for(int i=n+1;i>=1;i--)
{
int P=Cp[i-1];
for(int j=0;j<=n&&j<=P&&(i*j<=n);j++)
{
for(int k=0;k<=P;k++)
{
if(!dp[i][j][k])
{
continue;
}
int Pw=1;
for(int t=1;t+j<=n&&k+(t*(i-1))<=P&&t<=P&&(P-k-t*(i-1))>=0;t++)
{
Pw=((long long)Pw*inv_fac[i-1])%MOD;
int DJ=dp[i][j][k];
DJ=((long long)DJ*C[P-j][t])%MOD;
DJ=((long long)DJ*fac[P-k])%MOD;
DJ=((long long)DJ*Pw)%MOD;
DJ=((long long)DJ*inv_fac[P-k-t*(i-1)])%MOD;
dp[i-1][t+j][k+(t*(i-1))]=((long long)dp[i-1][t+j][k+(t*(i-1))]+DJ)%MOD;
}
dp[i-1][j][k]=((long long)dp[i-1][j][k]+dp[i][j][k])%MOD;
}
}
}
printf("%d",dp[0][n][n]);
}
D
\(Prufer\)序列
首先计算有多少个满足条件的数,这个毫无疑问就是\(\dfrac{(n-2)!d_1}{\prod d_i}\)
然后考虑计算每个节点作为好节点的贡献
首先对于节点\(i\),作为好的节点它内部子树的节点大小必须\(>i\),同时节点度数和必须为节点数\(-1\)
根据这个我们可以用\(dp_{i,j,k}\)计算出如果\(i\)的子树内有\(j\)个点时度数为\(k\)的方案数,如果子树大小为\(j\)时必须满足\(k=j-d_i\)
然后这里我们考虑计算子树\(i\)内的排列方式和子树外的排列方式(把\(i\)的子树看作一个点),也即是\(\dfrac{d_1d_i(n-j-2)!(j-1)!}{\prod d_i}\)
注意点数为\(1\)的特判一下
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MOD=998244353;
const int MAXN=505;
int Pow(int a,int b,int p)
{
int res=1;
int base=a;
while(b)
{
if(b&1)
{
res=((long long)res*base)%p;
}
base=((long long)base*base)%p;
b>>=1;
}
return res;
}
int inv(int a,int p)
{
return Pow(a,p-2,p);
}
int n;
int d[MAXN];
int fac[MAXN];
int dp[MAXN][MAXN][MAXN];
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&n);
fac[0]=1;
for(int i=1;i<=n;i++)
{
fac[i]=((long long)fac[i-1]*i)%MOD;
}
for(int i=1;i<=n;i++)
{
scanf("%d",&d[i]);
}
dp[n+1][0][0]=1;
for(int i=n;i>=1;i--)
{
for(int j=0;j<=n;j++)
{
for(int k=0;k<=n;k++)
{
if(dp[i+1][j][k])
{
dp[i][j][k]=((long long)dp[i][j][k]+dp[i+1][j][k])%MOD;
dp[i][j+1][k+d[i]]=((long long)dp[i][j+1][k+d[i]]+dp[i+1][j][k])%MOD;
}
}
}
}
int Inv=1;
for(int i=1;i<=n;i++)
{
Inv=((long long)Inv*fac[d[i]])%MOD;
}
Inv=inv(Inv,MOD);
int Rty=((long long)fac[n-2]*d[1])%MOD;
Rty=((long long)Rty*Inv)%MOD;
int Res=Rty;
for(int i=2;i<=n;i++)
{
if(d[i]==0)
{
Res=((long long)Res+Rty)%MOD;
continue;
}
for(int j=d[i];j<=n-i;j++)
{
int ep=j-d[i];
if(ep>=0)
{
int Rt=dp[i+1][j][ep];
if(!Rt)
{
continue;
}
Rt=((long long)Rt*Inv)%MOD;
Rt=((long long)Rt*fac[j-1])%MOD;
Rt=((long long)Rt*d[i])%MOD;
Rt=((long long)Rt*d[1])%MOD;
Rt=((long long)Rt*fac[n-j-2])%MOD;
Res=((long long)Res+Rt)%MOD;
}
}
}
printf("%d\n",Res);
}
ARC163
A
显然划分两次最优,直接枚举即可
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=2005;
int t;
int n;
char s[MAXN];
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&t);
while(t--)
{
scanf("%d",&n);
scanf("%s",s+1);
// for(int i=1;i<=n;i++)
// {
// printf("%c",s[i]);
// }
// printf("\n");
bool f=0;
for(int i=2;i<=n;i++)
{
string S,T;
S.clear();
T.clear();
for(int j=1;j<i;j++)
{
S+=s[j];
}
for(int j=i;j<=n;j++)
{
T+=s[j];
}
// cout<<T<<endl;
// cout<<S<<' '<<T<<endl;
if(S<T)
{
f=1;
}
}
if(f)
{
printf("Yes\n");
}
else
{
printf("No\n");
}
}
}
B
直接枚举\(a_1\),然后二分找到最小\(a_2\)的位置,线段树维护一下
两个\(log\)有点卡常
Show Code
#include<bits/stdc++.h>
#define ls Tree[p].lc
#define rs Tree[p].rc
using namespace std;
const int MAXN=2e5+5;
int n;
int m;
int A[MAXN];
struct Seg{
int date,lc,rc;
}Tree[MAXN*30];
int rt;
int cnt_node;
void Insert(int &p,int l,int r,int k)
{
if(!p)
{
p=++cnt_node;
}
Tree[p].date++;
if(l==r)
{
return;
}
int mid=(l+r)>>1;
if(k<=mid){
Insert(ls,l,mid,k);
}
else
{
Insert(rs,mid+1,r,k);
}
}
int Query(int p,int l,int r,int ql,int qr)
{
if(!p)
{
return 0;
}
if(l>=ql&&r<=qr)
{
return Tree[p].date;
}
int Res=0;
int mid=(l+r)>>1;
if(ql<=mid)
{
Res+=Query(ls,l,mid,ql,qr);
}
if(qr>mid)
{
Res+=Query(rs,mid+1,r,ql,qr);
}
return Res;
}
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d %d",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%d",&A[i]);
}
for(int i=3;i<=n;i++)
{
Insert(rt,1,1e9,A[i]);
}
int Res=2e9;
for(int i=1;i<=n;i++)
{
int l=A[i];
int r=1e9;
int Key=-1;
while(l<=r)
{
int mid=(l+r)>>1;
if(Query(rt,1,1e9,A[i],mid)>=m)
{
r=mid-1;
Key=mid;
}
else
{
l=mid+1;
}
}
if(Key!=-1)
{
int Tot=max(0,A[1]-A[i])+max(0,Key-A[2]);
Res=min(Res,Tot);
}
}
printf("%d",Res);
}
C
首先有\(\dfrac{1}{n(n+1)}=\dfrac{1}{n}-\dfrac{1}{n+1}\)
有个比较显的思路,考虑\(a_i=\dfrac{1}{i(i+1)},a_n=\dfrac{1}{n}\)
唯一的问题在于\(n\)在之前被访问过
实际上直接整体\(\times\dfrac{1}{2}\)再用个\(\dfrac{1}{2}\)即可
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=505;
int T;
int n;
int Vis[MAXN*MAXN];
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&T);
while(T--)
{
scanf("%d",&n);
for(int i=1;i<n;i++)
{
Vis[i*(i+1)]=1;
}
if(n==2)
{
printf("No\n");
}
else if(!Vis[n])
{
printf("Yes\n");
for(int i=1;i<n;i++)
{
printf("%d ",i*(i+1));
}
printf("%d\n",n);
}
else
{
printf("Yes\n2 ");
for(int i=1;i<n-1;i++)
{
printf("%d ",2*i*(i+1));
}
printf("%d\n",2*(n-1));
}
for(int i=1;i<n;i++)
{
Vis[i*(i+1)]=0;
}
}
}
D
竞赛图有个性质是缩点后拓扑序已经确定了
考虑把拓扑序拉出来,\(s_1,s_2,s_3,s_4....s_k\)
对于\(s_i,s_{i+1}\),我们可以将\([1,i]\)化分为一个点集\(A\),\([i+1,k]\)划分成另一个点集\(B\),满足两点集之间的边都是\(A\rightarrow B\)
可以发现任意合法的点集划分对应这一个分割点\(i\)
于是直接考虑对点集划分计数,设\(dp_{i,j,k}\)表示前\(i+j\)个点,有\(i\)个点分到\(A\),\(j\)个点分到\(B\)其中有\(k\)对小指大的方案
转移就直接枚举\(A/B\)中的连边情况,注意一下\(i+j\)归到\(B\)时\(k\)要\(+i\)
Show Code
// LUOGU_RID: 120168019
#include<bits/stdc++.h>
using namespace std;
const int MOD=998244353;
const int MAXN=55;
int n;
int m;
int dp[MAXN][MAXN][MAXN*MAXN];
int C[MAXN*MAXN][MAXN*MAXN];
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d %d",&n,&m);
C[0][0]=1;
for(int i=1;i<=n*n;i++)
{
C[i][0]=1;
for(int j=1;j<=i;j++)
{
C[i][j]=((long long)C[i-1][j]+C[i-1][j-1])%MOD;
}
}
dp[0][0][0]=1;
for(int i=0;i<=n;i++)
{
for(int j=0;(i+j)<=n;j++)
{
for(int k=0;k<=m;k++)
{
if(!dp[i][j][k])
{
continue;
}
for(int t=0;t<=i;t++)
{
dp[i+1][j][k+t]=((long long)dp[i+1][j][k+t]+((long long)dp[i][j][k]*C[i][t])%MOD)%MOD;
}
for(int t=0;t<=j;t++)
{
dp[i][j+1][k+t+i]=((long long)dp[i][j+1][k+t+i]+((long long)dp[i][j][k]*C[j][t])%MOD)%MOD;
}
}
}
}
int Res=(MOD-C[(n*(n-1))/2][m]);
for(int i=0;i<=n;i++)
{
Res=((long long)Res+dp[i][n-i][m])%MOD;
}
printf("%d\n",Res);
}
ARC149
A
直接记录\(1111..\)然后\(check\)一下即可
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=1e5+5;
int n;
int m;
int Mtl[MAXN];
signed main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d %d",&n,&m);
for(int i=1;i<=n;i++)
{
Mtl[i]=((long long)Mtl[i-1]*10+1)%m;
}
for(int len=n;len>=1;len--)
{
for(int x=9;x>=1;x--)
{
if(((long long)Mtl[len]*x)%m==0)
{
for(int i=1;i<=len;i++)
{
printf("%d",x);
}
return 0;
}
}
}
printf("-1");
}
B
捆绑着任意排序
我猜最大值是\(A\)排序\(B\)乱序/\(B\)排序\(A\)乱序
证明的话考虑调整法,如果\(A\)有一个数不在\(LIS\)里就把它插进去,这样一定不劣
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=3e5+5;
struct node{
int A,B;
}a[MAXN];
bool cmp(node x,node y)
{
return x.A<y.A;
}
bool kmp(node x,node y)
{
return x.B<y.B;
}
int n;
int Bit[MAXN];
int lowbit(int x)
{
return x&(-x);
}
void update(int k,int x)
{
for(int i=k;i<=n;i+=lowbit(i))
{
Bit[i]=max(Bit[i],x);
}
}
int Q(int k)
{
int res=0;
for(int i=k;i>=1;i-=lowbit(i))
{
res=max(res,Bit[i]);
}
return res;
}
signed main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i].A);
}
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i].B);
}
sort(a+1,a+1+n,cmp);
int Res=0;
for(int i=1;i<=n;i++)
{
int kp=Q(a[i].B)+1;
Res=max(Res,kp+n);
update(a[i].B,kp);
}
memset(Bit,0,sizeof(Bit));
sort(a+1,a+1+n,kmp);
for(int i=1;i<=n;i++)
{
int kp=Q(a[i].A)+1;
Res=max(Res,kp+n);
update(a[i].A,kp);
}
printf("%d\n",Res);
}
C
偶数前半部分一起,奇数放后半部分
交接处偶数满足\(\bmod 3=2\),奇数满足\(\bmod 3=1\)
这样\(n\ge 6\)可以满足
剩下的特判即可
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=1e6+5;
int n;
int vis[MAXN];
bool Ck(int x)
{
for(int i=2;i*i<=x;i++)
{
if(x%i==0)
{
return 1;
}
}
return 0;
}
signed main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&n);
if(n==3)
{
printf("5 3 1\n");
printf("9 7 8\n");
printf("6 2 4\n");
return 0;
}
vector<int>Odd;
vector<int>Even;
vector<int>odd;
vector<int>even;
for(int i=1;i<=n*n;i++)
{
if(i&1)
{
if(i%3==1)
{
Odd.push_back(i);
}
}
else
{
if(i%3==2)
{
Even.push_back(i);
}
}
}
int Mt=min(Even.size(),Odd.size());
Mt=min(Mt,n);
for(int i=0;i<Mt;i++)
{
vis[Odd[i]]=1;
}
for(int i=0;i<Mt;i++)
{
vis[Even[i]]=1;
}
while(Even.size()>Mt)
{
Even.pop_back();
}
while(Odd.size()>Mt)
{
Odd.pop_back();
}
reverse(Odd.begin(),Odd.end());
if(Mt!=n)
{
//cerr<<"fuck"<<endl;
for(int i=1;i<=n*n;i+=2)
{
for(int j=2;j<=n*n;j+=2)
{
if(Odd.size()==n)
{
break;
}
if(vis[i])
{
continue;
}
if(vis[j])
{
continue;
}
if(Ck(i+j))
{
Odd.push_back(i);
vis[i]=1;
Even.push_back(j);
vis[j]=1;
}
}
}
//cerr<<"fuck"<<endl;
}
for(int i=1;i<=n*n;i++)
{
if(i&1)
{
if(vis[i])
{
continue;
}
odd.push_back(i);
}
else
{
if(vis[i])
{
continue;
}
even.push_back(i);
}
}
if(n&1)
{
for(int i=1;i<=n/2;i++)
{
for(int j=1;j<=n;j++)
{
if(even.empty())
{
break;
}
printf("%d ",even.back());
even.pop_back();
}
if(even.empty())
{
for(int j=n/2+1;j<=n;j++)
{
printf("%d ",Even[j-n/2-1]);
}
}
printf("\n");
}
for(int i=1;i<=n/2;i++)
{
printf("%d ",Even[i+n/2]);
}
for(int i=n/2+1;i<=n;i++)
{
printf("%d ",Odd[i-n/2-1]);
}
printf("\n");
for(int i=1;i<=n/2;i++)
{
for(int j=1;j<=n;j++)
{
if(i==1&&j<=(n/2))
{
printf("%d ",Odd[j+n/2]);
}
else
{
printf("%d ",odd.back());
odd.pop_back();
}
}
printf("\n");
}
}
else
{
//cerr<<Odd.size()<<' '<<Even.size()<<endl;
for(int i=1;i<n/2;i++)
{
for(int j=1;j<=n;j++)
{
printf("%d ",even.back());
even.pop_back();
}
printf("\n");
}
for(int i=0;i<n;i++)
{
printf("%d ",Even[i]);
}
printf("\n");
for(int i=0;i<n;i++)
{
printf("%d ",Odd[i]);
}
printf("\n");
for(int i=1;i<n/2;i++)
{
for(int j=1;j<=n;j++)
{
printf("%d ",odd.back());
odd.pop_back();
}
printf("\n");
}
}
}
D
DJNB!!
考虑这个过程\([-D_i,D_i]\)这个区间的数相当于是直接交换
\([-\infin,-D_i],[D_i,\infin]\)平移一下
这样处理很麻烦
考虑\([-D_i,0),(0,D_i]\)是对称的,值也是相反数关系,我们可以直接删除\([-D_i,0)\)用带权并查集维护
这样我们就可以直接平移原点了,删除原点左边/右边的数并合并即可
Show Code
// LUOGU_RID: 119069522
#include<bits/stdc++.h>
using namespace std;
const int MAXN=2e6+5;
const int MAXM=2e6+5;
int m;
int n;
int X[MAXN];
int D[MAXN];
int L[MAXM];
int fa[MAXM];
int dep[MAXM];
int find(int x)
{
if(fa[x]==x)
{
return fa[x];
}
int s=fa[x];
fa[x]=find(fa[x]);
dep[x]=dep[s]^dep[x];
return fa[x];
}
void unionn(int i,int j)
{
int ex=find(i);
int ey=find(j);
fa[ex]=ey;
dep[ex]=(dep[j]^dep[i]^1);
}
pair<int,int>Ans[MAXM];
signed main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d %d",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%d",&X[i]);
L[X[i]]=i;
Ans[i].first=0;
}
for(int i=1;i<=m;i++)
{
scanf("%d",&D[i]);
}
int Pi=0;
int l=1;
int r=1e6;
for(int i=l;i<=r;i++)
{
fa[i]=i;
dep[i]=0;
}
for(int i=1;i<=m;i++)
{
if(Pi>r)
{
Pi-=D[i];
if(Pi<=1e6&&Pi>0&&(!Ans[Pi].first))
{
Ans[Pi].first=1;
Ans[Pi].second=i;
}
if(Pi>=l&&Pi<=r)
{
if(Pi-l>r-Pi)
{
for(int i=Pi+1;i<=r;i++)
{
int To=2*Pi-i;
unionn(i,To);
}
r=Pi-1;
}
else
{
for(int i=l;i<=Pi-1;i++)
{
int To=2*Pi-i;
unionn(i,To);
}
l=Pi+1;
}
}
}
else if(Pi<l)
{
Pi+=D[i];
if(Pi<=1e6&&Pi>0&&(!Ans[Pi].first))
{
Ans[Pi].first=1;
Ans[Pi].second=i;
}
if(Pi>=l&&Pi<=r)
{
if(Pi-l>r-Pi)
{
for(int i=Pi+1;i<=r;i++)
{
int To=2*Pi-i;
unionn(i,To);
}
r=Pi-1;
}
else
{
for(int i=l;i<=Pi-1;i++)
{
int To=2*Pi-i;
unionn(i,To);
}
l=Pi+1;
}
}
}
//printf("%d %d??\n",)
}
for(int i=1;i<=n;i++)
{
//printf("%d %d\n",X[i],find(X[i]));
if(Ans[find(X[i])].first)
{
printf("Yes %d\n",Ans[find(X[i])].second);
}////
else
{
int Gk=find(X[i])-Pi;
// if(i==n)
// {
// printf("%d????\n",dep[X[i]]);
// }
if(dep[X[i]])
{
Gk*=-1;
}
printf("No %d\n",Gk);
}
}
}
ARC155
A
模拟一下你会发现这个长度为\(k\)子串\(T\)会在左右依次填\(S,S^{rev}\)
这个我们可以直接让\(k\bmod 2n\)(最开始\(\bmod n\)了\kk)
然后你会发现填到最后就是\(T\)前\(n\)个\(S^{rev}\),后面\(S\)
直接\(check\)一下即可
Show Code
#include<bits/stdc++.h>
#define int long long
using namespace std;
int T;
long long k;
int n;
string s;
signed main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%lld",&T);
while(T--)
{
scanf("%lld %lld",&n,&k);
k%=2*n;
cin>>s;
string t;
t.resize(k,'.');
for(int i=0;i<k;i++)
{
if(!(i/n))
{
t[i]=s[n-(i%n)-1];
}
else
{
t[i]=s[i%n];
}
}
//cout<<t<<endl;
string A=s+t;
string B=t+s;
int C=A.size();
bool f=1;
for(int i=0;i<A.size();i++)
{
int To=C-i-1;
if(A[i]!=A[To])
{
f=0;
}
if(B[i]!=B[To])
{
f=0;
}
}
if(f)
{
printf("Yes\n");
}
else
{
printf("No\n");
}
}
}
B
注意到\(||a-x|-b|=min(|x-(a+b)|,|x-(a-b)|)\)
然后就把它拆成\((a+b),(a-b)\)用\(set\)维护即可
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=2e5+5;
int Q;
int A,B;
int t,a,b;
set<int>s;
signed main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d %d %d",&Q,&A,&B);
s.insert(A+B);
s.insert(A-B);
//printf("%d %d\n",A+B,A-B);
while(Q--)
{
scanf("%d %d %d",&t,&a,&b);
if(t==1)
{
s.insert(a-b);
s.insert(a+b);
// printf("%d %d\n",a-b,a+b);
}
else
{
int Res=0x3f3f3f3f;
auto it=s.lower_bound(a);
if((it!=s.end()))
{
if((*it)<=b)
{
Res=0;
}
else
{
Res=min(Res,(*it)-a);
}
}
it=s.upper_bound(a);
if(it!=s.begin())
{
--it;
Res=min(Res,a-(*it));
}
it=s.upper_bound(b);
if(it!=s.begin())
{
--it;
if((*it)>=a)
{
Res=0;
}
else
{
Res=min(Res,b-(*it));
}
}
it=s.lower_bound(b);
if(it!=s.end())
{
Res=min(Res,(*it)-b);
}
printf("%d\n",Res);
}
}
}
C
操作一定是三个偶数或者是两奇一偶
如果存在两奇一偶说明所有奇数可以自由滑动
事实上这种情况只要满足偶数个数\(\ge 2\)就能任意排序
考虑一次性把奇数全部提到最前面,然后在取一个奇数出来
如果不能自由滑动,说明可以用奇数划分,每个块内自由排序
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=2e5+5;
int n;
int A[MAXN];
int B[MAXN];
int Ap[MAXN];
int Bp[MAXN];
int main()
{
scanf("%d",&n);
vector<int>odd;
vector<int>even;
for(int i=1;i<=n;i++)
{
scanf("%d",&A[i]);
Ap[i]=A[i];
if(A[i]&1)
{
odd.push_back(i);
}
else
{
even.push_back(i);
}//////
}
vector<int>Even;
vector<int>Odd;
for(int i=1;i<=n;i++)
{
scanf("%d",&B[i]);
Bp[i]=B[i];
if(B[i]&1)
{
Odd.push_back(i);
}
else
{
Even.push_back(i);
}
}
sort(Ap+1,Ap+1+n);
sort(Bp+1,Bp+1+n);
bool fou=1;
for(int i=1;i<=n;i++)
{
if(Ap[i]!=Bp[i])
{
fou=0;
}
}
if(!fou)
{
printf("No");
return 0;
}
bool found=0;
for(int i=1;i<odd.size();i++)
{
if((odd[i]==odd[i-1]+1)||(odd[i]==odd[i-1]+2))
{
found=1;
}
}
bool Found=0;
for(int i=1;i<odd.size();i++)
{
if((Odd[i]==Odd[i-1]+1)||(Odd[i]==Odd[i-1]+2))
{
Found=1;
}
}
if(!Even.size())
{
found=0;
Found=0;
}
if(found&&Found)
{
if(Even.size()>2)
{
printf("Yes");
}
else
{
int f=1;
for(int i=0;i<even.size();i++)
{
if(A[even[i]]!=B[Even[i]])
{
f=0;
}
}
if(f)
{
printf("Yes");
}
else
{
printf("No");
}
}
}
else if((!Found)&&(!found))
{
bool f=1;
for(int i=0;i<Odd.size();i++)
{
if(B[Odd[i]]!=A[odd[i]])
{
f=0;
}
if(Odd[i]!=odd[i])
{
f=0;
}
}
if(!f)
{
printf("No");
}
else
{
for(int i=0;i<Odd.size();i++)
{
if(i==0)
{
int l=1;
int r=Odd[i]-1;
if(r-l+1>2)
{
}
else
{
for(int j=l;j<=r;j++)
{
if(A[j]!=B[j])
{//
f=0;
}
}
}
}
else
{
int l=Odd[i-1]+1;
int r=Odd[i]-1;
if(r-l+1>2)
{
}
else
{
for(int j=l;j<=r;j++)
{
if(A[j]!=B[j])
{
f=0;
}
}
}
}
if(i==Odd.size()-1)
{
int l=Odd[i]+1;
int r=n;
if(r-l+1>2)
{
}
else
{
for(int j=l;j<=r;j++)
{
if(A[j]!=B[j])
{
f=0;
}
}
}
}
}
if(f)
{
printf("Yes");
}
else
{
printf("No");
}
}
}
else
{
printf("No");
}
}
D
nknb!!!!(话说nk一眼秒)
考虑前面选的数一定是当前\(G\)的倍数
下一步决策要么\(G\rightarrow G',(G'|G),\exist x,gcd(k,G)=G'\)
要么\(G\rightarrow G\)
这里的\(G\rightarrow G\)如果没有的话似乎就可以直接\(dp\)了,我们只需要找到是否存在这样的\(k\),因为这里用了一个\(k\)并不会对后续选择产生影响,这里可以容斥计算个数,对于\(G\)我们从大到小枚举\(G'\)并在后面减去\(G'\)的贡献
如果有呢?
实际上只需要在状态中加入当前是\(G\)的倍数的还有奇数/偶数个
Show Code
// LUOGU_RID: 118979939
#include<bits/stdc++.h>
using namespace std;
const int MAXN=2e5+5;
int n;
int A[MAXN];
int C[MAXN];
vector<int>V[MAXN];
int D[MAXN];
int dp[MAXN][2];
signed main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&A[i]);
C[A[i]]++;
}
for(int i=1;i<=MAXN-5;i++)
{
for(int j=2*i;j<=MAXN-5;j+=i)
{
V[j].push_back(i);
C[i]+=C[j];
}
}
for(int i=1;i<=MAXN-5;i++)
{
reverse(V[i].begin(),V[i].end());
}
for(int i=1;i<=MAXN-5;i++)
{
if(i==1)
{
dp[i][0]=1;
dp[i][1]=1;
continue;
}
for(int j=0;j<V[i].size();j++)
{
D[V[i][j]]=C[V[i][j]]-C[i];
}
for(int j=0;j<V[i].size();j++)
{
if(D[V[i][j]]>0)
{
//printf("%d %d %d??\n",i,V[i][j],dp[V[i][j]][0]);
if(!dp[V[i][j]][0])
{
dp[i][(C[i]&1)^(C[V[i][j]]&1)^1]=1;
}
if(!dp[V[i][j]][1])
{
dp[i][(C[i]&1)^(C[V[i][j]]&1)]=1;
}
}
for(int k=0;k<V[V[i][j]].size();k++)
{
D[V[V[i][j]][k]]-=D[V[i][j]];
}
}
if((!dp[i][0]))
{
dp[i][1]=1;
}
}
for(int i=1;i<=n;i++)
{
if(!dp[A[i]][(C[A[i]]-1)&1])
{
printf("Takahashi\n");
}
else
{
printf("Aoki\n");
}
}
}
E
最开始以为是一位一位得搞,不过很多位实际上可以分开了搞,但还是没想到线性基
首先如果我们\(S\)有一个线性基\(B\),我们可以把\(B_1\)及它能表示的数全部放进\(T_1\),剩下的放进\(T2\),可以发现这样\(B_1\)这个基被削去了
注意\(T2\)放进去之后线性基大小可能会变,但如果\(S\)中有\(0\)一定不会变
如果我们给所有数异或一个\(x\),答案不会变,所以我们给所有数先异或个\(a_1\)
我们一次操作最好也就是减少一个基,因此答案就是初始时线性基的大小
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=305;
int n,m;
bitset<MAXN>B[MAXN];
bitset<MAXN>a[MAXN];
int Res=0;
void Insert(bitset<MAXN>x)
{
for(int i=m;i>=0;i--)
{
if(x[i])
{
if(B[i][i])
{
x^=B[i];
}
else
{
B[i]=x;
++Res;
break;
}
}
}
}
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d %d",&n,&m);
bool f=0;
for(int i=1;i<=n;i++)
{
cin>>a[i];
if(!(a[i].any()))
{
f=1;
}
}
for(int i=2;i<=n;i++)
{
a[i]^=a[1];
}
if(n==1)
{
if(f)
{
printf("0");
}
else
{
printf("1");
}
return 0;
}
for(int i=2;i<=n;i++)
{
Insert(a[i]);
}
printf("%d\n",Res);
}
ARC160
A
一眼没思路/kk
对于操作\((l1,r1)\),\((l2,r2)\)我们是可以直接比较两者之间的大小的
然后用\(nth\_element\)即可
好像有\(O(nlog(n))\)做法
就是考虑每个位置的答案是什么,如果确定了前\(i-1\)个是没变的时候取答案,第\(i\)位的答案要么是和后面的交换要么也是不变,这个大概二分一下就可以了
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=7005;
int n,k;
int A[MAXN];
struct Node{
int l,r;
bool operator<(const Node x)const{
if(l==x.l)
{
return A[r]<A[x.r];
}
else
{
if(((l<x.l)&&(l!=r))||(x.l==x.r))
{
return A[r]<A[l];
}
else
{
return A[x.r]>A[x.l];
}
}
}
}a[MAXN*MAXN];
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d %d",&n,&k);
for(int i=1;i<=n;i++)
{
scanf("%d",&A[i]);
}
int Cnt=0;
for(int l=1;l<=n;l++)
{
for(int r=l;r<=n;r++)
{
a[++Cnt].l=l;
a[Cnt].r=r;
}
}
nth_element(a+1,a+k,a+1+Cnt);
for(int i=1;i<a[k].l;i++)
{
printf("%d ",A[i]);
}
for(int i=a[k].r;i>=a[k].l;i--)
{
printf("%d ",A[i]);
}
for(int i=a[k].r+1;i<=n;i++)
{
printf("%d ",A[i]);
}
}
B
首先肯定最多只有一个数\(>\sqrt n\)
然后钦定\(x\le y\le z\),枚举\(y\),则\(z\le\lfloor\dfrac{n}{y}\rfloor\)
注意相同即可
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MOD=998244353;
int T;
int n;
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&T);
while(T--)
{
scanf("%d",&n);
int Res=0;
for(int i=1;i*i<=n;i++)
{
int Lit=(n/i);
int Rp=((long long)(i-1)*(Lit-i))%MOD;
Rp=((long long)Rp*6)%MOD;
Res=((long long)Res+Rp)%MOD;
Rp=(Lit-i);
Rp=((long long)Rp*3)%MOD;
Res=((long long)Res+Rp)%MOD;
Rp=(i-1);
Rp=((long long)Rp*3)%MOD;
Res=((long long)Res+Rp)%MOD;
Rp=1;
Res=((long long)Res+Rp)%MOD;
}
printf("%d\n",Res);
}
}
C
简单\(dp\),注意到状态数不超过\(nlog(n)\)即可
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MOD=998244353;
const int MAXN=4e5+5;
int n;
int x;
int A[MAXN];
int dp[MAXN];
int Sum[MAXN];
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&x);
A[x]++;
}
dp[0]=1;
for(int i=2;i<=MAXN-5;i++)
{
int Mk=0;
for(int j=0;;j++)
{
if(!dp[j])
{
Mk=j-1;
break;
}
}
Sum[Mk+1]=0;
for(int j=Mk;j>=0;j--)
{
Sum[j]=((long long)Sum[j+1]+dp[j])%MOD;
dp[j]=0;
}
for(int j=0;j<=(A[i-1]+Mk)/2;j++)
{
dp[j]=Sum[max(0,2*j-A[i-1])];
}
}
printf("%d\n",dp[0]);
}
D
明显要倒着来
这里不好对\(A\)计数,考虑直接对操作序列计数,但可能会算重
实际上,直接限制每个区间加的次数\(<k\)即可
设\(f_i\)为\([1,i+k-1]\)加的次数,\(g_i\)为\(i\)加的次数
于是问题转换为满足\(\sum\limits_{i=1}^{n-k+1}f_i+\sum\limits_{i=1}^ng_i=\dfrac{m}{k},f_i<k\)的个数
然后这个经典容斥,钦定有\(i\)个数先取了\(k\)个即可
答案为\(\sum\limits_{i=0}^{n-k+1}(-1)^i\binom{n-k+1}{i}\binom{2n-k+\frac{m}{k}-ki}{2n-k}\)
Show Code
// LUOGU_RID: 118704316
#include<bits/stdc++.h>
using namespace std;
const int MOD=998244353;
int Pow(int a,int b,int p)
{
int res=1;
int base=a;
while(b)
{
if(b&1)
{
res=((long long)res*base)%p;
}
base=((long long)base*base)%p;
b>>=1;
}
return res;
}
int inv(int a,int p)
{
return Pow(a,p-2,p);
}
int n,k;
long long m;
int C(long long n,int m)
{
if(m<0||n<m)
{
return 0;
}
if((m==0)||(n==m))
{
return 1;
}
int res=1;
for(long long i=n-m+1;i<=n;i++)
{
res=((long long)res*((i%MOD)))%MOD;
}
int tes=1;
for(int i=1;i<=m;i++)
{
tes=((long long)tes*i)%MOD;
}
res=((long long)res*inv(tes,MOD))%MOD;
return res;
}
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
int Res=0;
scanf("%d %lld %d",&n,&m,&k);
if(m%k)
{
printf("0");
}
else
{
m/=k;
for(int i=0;i<=n-k+1;i++)
{
int Rp=C(n-k+1,i);
Rp=((long long)Rp*C(2*n-k+m-i*k,2*n-k))%MOD;
if(i&1)
{
Res=((long long)Res-Rp+MOD)%MOD;
}
else
{
Res=((long long)Res+Rp)%MOD;
}
}
printf("%d\n",Res);
}
}
E
每个叶子肯定要选
设叶子个数为\(k\)
对于一颗二叉树,一定能找出一个点满足删除这个点后每个子树内的叶子个数小于\(\dfrac{k}{2}\),证明大概类似于树的重心
我们设这个点为\(u\)
然后如果\(k\)为偶数,我们可以每次选不同子树的两个点来构造,使得其构成若干个环至少有两个交点,因此答案可以直接取到下界
如果\(k\)为奇数,实际上可以钦定一个点和其他点相连,而这个点连出来的边要和其他环有两个点相交,实际上这里就是要求这个点\(x\)不能和\(x\)到第一个三度点路径上的点相连,直接枚举\(x\)用\(set\)维护即可
Show Code
// LUOGU_RID: 118785801
#include<bits/stdc++.h>
using namespace std;
const int MAXN=2e5+5;
int T;
int n;
int a[MAXN];
int x,y;
vector<int>g[MAXN];
int Siz[MAXN];
int Maxs[MAXN];
int Heart;
void dfs(int x,int f)
{
Siz[x]=(g[x].size()==1);
Maxs[x]=0;
for(int i=0;i<g[x].size();i++)
{
int v=g[x][i];
if(v==f)
{
continue;
}
dfs(v,x);
Maxs[x]=max(Maxs[x],Siz[v]);
Siz[x]+=Siz[v];
}
}
multiset<pair<int,int> >S;
int Res=0x3f3f3f3f;
int Fa[MAXN];
int Miu,Miv;
void find(int x,int f,int Last)
{
S.erase(S.find(make_pair(a[x],x)));
if(g[x].size()==1)
{
//printf("%d---\n",S.size());
int Tg=(*(S.begin())).second;
if(a[Tg]<Res)
{
Res=a[Tg];
Miu=x;
Miv=Tg;
}
}
for(int i=0;i<g[x].size();i++)
{
int v=g[x][i];
if(v==f)
{
continue;
}
Fa[v]=x;
if(g[v].size()==3)
{
int Now=x;
while(Now!=Fa[Last])
{
S.insert(make_pair(a[Now],Now));
Now=Fa[Now];
}
find(v,x,v);
Now=x;
while(Now!=Fa[Last])
{
S.erase(S.find(make_pair(a[Now],Now)));
Now=Fa[Now];
}
}
else
{
find(v,x,Last);
}
}
S.insert(make_pair(a[x],x));
}
vector<int>Leaf[MAXN];
int Ct=0;
void Get(int x,int f)
{
if(g[x].size()==1&&(x!=Miu))
{
Leaf[Ct].push_back(x);
}
for(int i=0;i<g[x].size();i++)
{
int v=g[x][i];
if(v==f)
{
continue;
}
Get(v,x);
}
}
int main()
{
// freopen("data.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&T);
while(T--)
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
g[i].clear();
}
S.clear();
Res=0x3f3f3f3f;
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
S.insert(make_pair(a[i],i));
}
for(int i=1;i<n;i++)
{
scanf("%d %d",&x,&y);
g[x].push_back(y);
g[y].push_back(x);
}
dfs(1,0);
for(int i=1;i<=n;i++)
{
Maxs[i]=max(Maxs[i],Siz[1]-Siz[i]);
if((g[i].size()>=2)&&(Maxs[i]<=(Siz[1]/2)))
{
Heart=i;
}
}
Miu=0;
//printf("%d??\n",Heart);
printf("%d\n",(Siz[1]+1)/2);
if(Siz[1]&1)
{
Fa[Heart]=0;
find(Heart,0,Heart);
printf("%d %d\n",Miu,Miv);
}
cerr<<Heart<<' '<<Siz[1]<<endl;
Ct=0;
priority_queue<pair<int,int> >q;
for(int i=0;i<g[Heart].size();i++)
{
int v=g[Heart][i];
++Ct;
Get(v,Heart);
if(Leaf[Ct].size())
{
q.push(make_pair(Leaf[Ct].size(),Ct));
}
}
while(q.size())
{
int tpx=q.top().second;
q.pop();
int tpy=q.top().second;
q.pop();
printf("%d %d\n",Leaf[tpx].back(),Leaf[tpy].back());
Leaf[tpx].pop_back();
Leaf[tpy].pop_back();
if(Leaf[tpx].size())
{
q.push(make_pair(Leaf[tpx].size(),tpx));
}
if(Leaf[tpy].size())
{
q.push(make_pair(Leaf[tpy].size(),tpy));
}
}
}
}
ARC157
A
简单分讨即可
Show Code
#include<bits/stdc++.h>
using namespace std;
int Abs(int x)
{
return x>0?x:-x;
}
int n;
int A,B,C,D;
int main()
{
scanf("%d %d %d %d %d",&n,&A,&B,&C,&D);
if(Abs(B-C)>1)
{
printf("No");
return 0;
}
if(B==0&&C==0)
{
if(A&&D)
{
printf("No");
return 0;
}
}
printf("Yes");
}
B
做法有点复杂,似乎是先把\(X\)变为\(Y\),如果变完了再把\(Y\)变\(X\),这里注意填完连续段的贡献会多一点
Show Code
#include<bits/stdc++.h>
using namespace std;
int n,k;
string s;
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d %d",&n,&k);
cin>>s;
int Res=0;
vector<int>Pos;
for(int i=0;i<n;i++)
{
if(s[i]=='Y')
{
Pos.push_back(i);
}
}
if(Pos.size()==n)
{
printf("%d\n",max(0,n-1-k));
return 0;
}
vector<int>si;
for(int i=1;i<Pos.size();i++)
{
int L=Pos[i-1]+1;
int R=Pos[i]-1;
si.push_back(R-L+1);
}
if(Pos.size()>=1)
{
//printf("ufkc\n");
int Po=Pos[0]+((n-1)-Pos.back());
sort(si.begin(),si.end());
for(int i=0;i<si.size();i++)
{
if(k>=si[i])
{
k-=si[i];
Res+=si[i]+1;
}
else
{
Res+=k;
k=0;
break;
}
}
if(k)
{
if(k<=Po)
{
Res+=k;
}
else
{
Res+=Po;
k-=Po;
if(k>0)
{
vector<int>Si;
Si.clear();
int Len=1;
int Op=0;
vector<int>BE;
BE.clear();
for(int i=1;i<Pos.size();i++)
{
if(Pos[i]==Pos[i-1]+1)
{
Len++;
}
else
{
if(Op)
{
Si.push_back(Len);
}
else
{
Op=1;
if(Len==Pos[i-1]+1)
{
BE.push_back(Len);
}
else
{
Si.push_back(Len);
}
}
Len=1;
}
}
if(Pos.back()==n-1)
{
BE.push_back(Len);
// printf("fuck\n");
}
else
{
if(Len==Pos.back()+1)
{
BE.push_back(Len);
}
else
{
Si.push_back(Len);
}
}
// printf("%d\n",BE.size());
if(BE.size())
{
for(int i=0;i<BE.size();i++)
{
int Lp=BE[i];
// printf("%d?\n",BE[i]);
if(Lp<k)
{
k-=Lp;
Res-=Lp;
}
else
{
Res-=k;
k=0;
break;
}
}
}
sort(Si.begin(),Si.end());
for(int i=Si.size()-1;i>=0;i--)
{
if(!k)
{
break;
}
int Lp=Si[i];
if(Lp<k)
{
k-=Lp;
Res-=(Lp+1);
}
else
{
Res-=(k+1);
k=0;
break;
}
}
}
}
}
printf("%d\n",Res);
}
else
{
printf("%d",max(0,k-1));
}
}
C
简单DP
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MOD=998244353;
const int MAXN=2e3+5;
int n,m;
string s[MAXN];
int dp1[MAXN][MAXN];
int dp2[MAXN][MAXN];
int dp3[MAXN][MAXN];
int main()
{
scanf("%d %d",&n,&m);
for(int i=0;i<n;i++)
{
cin>>s[i];
}
dp1[0][0]=0;
dp2[0][0]=0;
dp3[0][0]=1;
for(int i=0;i<n;i++)
{
for(int j=0;j<m;j++)
{
if(i==0&&j==0)
{
continue;
}
int nx=i-1;
int ny=j;
if(nx>=0&&ny>=0)
{
if(s[nx][ny]=='Y'&&s[i][j]=='Y')
{
dp1[i][j]=((long long)dp1[i][j]+((long long)2*dp2[nx][ny])%MOD)%MOD;
dp1[i][j]=((long long)dp1[i][j]+dp3[nx][ny])%MOD;
dp2[i][j]=((long long)dp2[i][j]+dp3[nx][ny])%MOD;
}
dp1[i][j]=((long long)dp1[i][j]+dp1[nx][ny])%MOD;
dp2[i][j]=((long long)dp2[i][j]+dp2[nx][ny])%MOD;
dp3[i][j]=((long long)dp3[i][j]+dp3[nx][ny])%MOD;
}
nx=i;
ny=j-1;
if(nx>=0&&ny>=0)
{
if(s[nx][ny]=='Y'&&s[i][j]=='Y')
{
dp1[i][j]=((long long)dp1[i][j]+((long long)2*dp2[nx][ny])%MOD)%MOD;
dp1[i][j]=((long long)dp1[i][j]+dp3[nx][ny])%MOD;
dp2[i][j]=((long long)dp2[i][j]+dp3[nx][ny])%MOD;
}
dp1[i][j]=((long long)dp1[i][j]+dp1[nx][ny])%MOD;
dp2[i][j]=((long long)dp2[i][j]+dp2[nx][ny])%MOD;
dp3[i][j]=((long long)dp3[i][j]+dp3[nx][ny])%MOD;
}
}
}
printf("%d",dp1[n-1][m-1]);
}
//2 2
//YY
//YY
D
之前一直往\(dp\)的方向想,结果就是个暴力、
实际上这玩意我们横着切一刀分出来的每一块的\(Y\)个数是一样的
直接枚举横着切了多少刀,这个时间复杂度感觉是\(n\),但实际上大概不超过\(100\)个比较玄学
然后我们就可以得到每一刀切的范围
对于竖着切一刀,其实差不多,注意要满足每横着的一块分到两个即可
实现起来有点细节,时间复杂度也很玄学
Show Code
// LUOGU_RID: 118421079
#include<bits/stdc++.h>
using namespace std;
const int MOD=998244353;
const int MAXN=2005;
int n,m;
char s[MAXN][MAXN];
int Sum[MAXN][MAXN];
int PointL[MAXN];
int PointR[MAXN];/////
int PL[MAXN][MAXN];
int PR[MAXN][MAXN];
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d %d",&n,&m);
int Tot=0;
for(int i=1;i<=n;i++)
{
scanf("%s",s[i]+1);
for(int j=1;j<=m;j++)
{
Sum[i][j]=Sum[i-1][j]+Sum[i][j-1]-Sum[i-1][j-1];
if(s[i][j]=='Y')
{
++Tot;
Sum[i][j]++;
}
}
}
if((Tot&1)||(!Tot))
{
printf("0");
}
else
{
int Res=0;
for(int x=1;x<=(n*m)/2&&x<=n;x++)
{
if((Tot/2)%x==0)
{
int Lix=(Tot/x);
int y=Lix/2;
int Liy=x*2;
int Last=0;
int Cx=0;
int res=1;
int i=1;
int Cp=1;
Last=i-1;
res=((long long)res*Cp)%MOD;
for(;i<=n;)
{
if(Sum[i][m]-Sum[Last][m]==Lix)
{
PointL[++Cx]=i;
Cp=1;
i++;
while(i<=n&&Sum[i][m]-Sum[i-1][m]==0)
{
++Cp;
i++;
}
if(Cx!=x)
{
res=((long long)res*Cp)%MOD;
}
Last=i-1;
PointR[Cx]=i-1;
}
else if(Sum[i][m]-Sum[Last][m]>Lix)
{
res=0;
break;
}
else
{
++i;
}
}
if(Cx!=x)
{
res=0;
//printf("???\n");
}
for(int i=1;i<=x;i++)
{
int j=1;
int Cy=0;
Last=j-1;
for(;j<=m;)
{
if((Sum[PointR[i]][j]-Sum[PointR[i-1]][j])-(Sum[PointR[i]][Last]-Sum[PointR[i-1]][Last])==2)
{
PL[i][++Cy]=j;
j++;
while(j<=m&&(Sum[PointR[i]][j]-Sum[PointR[i-1]][j])-(Sum[PointR[i]][j-1]-Sum[PointR[i-1]][j-1])==0)
{
j++;
}
Last=j-1;
PR[i][Cy]=j-1;
if(Cy==y)
{
PL[i][Cy]=m;
PR[i][Cy]=m;
}
}
else if((Sum[PointR[i]][j]-Sum[PointR[i-1]][j])-(Sum[PointR[i]][Last]-Sum[PointR[i-1]][Last])>2)
{
res=0;
break;
}
else
{
++j;
}
}
if(Cy!=y)
{
res=0;
//printf("%d %d???\n",x,Cy);
}
}
// printf("%d %d %d:::\n",x,y,res);
// for(int i=1;i<=x+1;i++)
// {
// for(int j=1;j<=y+1;j++)
// {
// printf("%d %d %d %d\n",i,j,PL[i][j],PR[i][j]);
// }
// }
for(int i=1;i<=y;i++)
{
int L=0;
int R=m;
for(int j=1;j<=x;j++)
{
L=max(PL[j][i],L);
R=min(PR[j][i],R);
}
if(L>R)
{
res=0;
}
else
{
res=((long long)res*(R-L+1))%MOD;
}
}
//printf("%d %d???\n",res,x);
Res=((long long)Res+res)%MOD;
}
}
printf("%d\n",Res);
}
}
E
没看到完全二叉树/kk
注意到是二叉树就简单了,可以发现\(C\)类的\(Y\)可以确定非叶子\(Y\)的个数是\(\dfrac{C}{2}\)
考虑如果根是\(Y\),那叶子上\(Y\)的个数就是\(B-\dfrac{C}{2}+1\),不是就是\(B-\dfrac{C}{2}\)
可以发现除了这些点都选\(X\)就满足条件了
然后可以发现\(Y\)就是最大独立集,可以设\(dp_{i,j,0/1}\)表示\(i\)为\(X/Y\)有\(j\)个叶子被选为\(Y\)时非叶子选为\(Y\)的最大个数
树上背包即可,\(1e8\)有点卡常
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=1e4+5;
int T;
int n,A,B,C;
int x,y;
vector<int>g[MAXN];
int dp[MAXN][2][MAXN/2+15];
int Leaf[MAXN];
void dfs(int x)
{
if(!((int)g[x].size()))
{
Leaf[x]=1;
dp[x][1][1]=0;
dp[x][0][0]=0;
return;
}
dp[x][0][0]=0;
dp[x][1][0]=1;
Leaf[x]=0;
for(int i=0;i<g[x].size();i++)
{
int v=g[x][i];
dfs(v);
for(int j=Leaf[x];j>=0;j--)
{
for(int k=Leaf[v];k>=0;k--)
{
dp[x][0][j+k]=max(dp[x][0][j+k],dp[x][0][j]+max(dp[v][0][k],dp[v][1][k]));
dp[x][1][j+k]=max(dp[x][1][j+k],dp[x][1][j]+dp[v][0][k]);
}
}
Leaf[x]+=Leaf[v];
}
}
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&T);
while(T--)
{
scanf("%d %d %d %d",&n,&A,&B,&C);
for(int i=1;i<=n;i++)
{
g[i].clear();
for(int j=0;j<=max(n/2,B-C/2+1);j++)
{
dp[i][0][j]=-0x3f3f3f3f;
dp[i][1][j]=-0x3f3f3f3f;
}
}
for(int i=2;i<=n;i++)
{
scanf("%d",&x);
g[x].push_back(i);
}
if(C&1)
{
printf("No\n");
}
else
{
int Q=C/2;
int P=B-Q;
dfs(1);
if((P>=0&&dp[1][0][P]>=Q)||((P+1)>=0&&dp[1][1][P+1]>=Q))
{
printf("Yes\n");
}
else
{
printf("No\n");
}
}
}
}
ARC154
A
似乎是均值反着用,直接最大乘最小即可
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MOD=998244353;
int n;
string A,B;
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&n);
cin>>A;
cin>>B;
int Mul=1;
int Res=0;
for(int i=n-1;i>=0;i--)
{
if(A[i]>B[i])
{
swap(A[i],B[i]);
}
}
int Ma=0,Mb=0;
for(int i=0;i<n;i++)
{
Ma=((long long)Ma*10+(A[i]-'0'))%MOD;
Mb=((long long)Mb*10+(B[i]-'0'))%MOD;
}
Res=((long long)Ma*Mb)%MOD;
printf("%d\n",Res);
return 0;
}
B
似乎很明显的二分,也明显有单调性
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=2e5+5;
int n;
char A[MAXN];
char B[MAXN];
int C[27];
int check(int x)
{
for(int i=0;i<26;i++)
{
C[i]=0;
}
for(int i=1;i<=x;i++)
{
C[A[i]-'a']++;
}
int Pi=x+1;
for(int i=1;i<=n;i++)
{
if(Pi<=n&&A[Pi]==B[i])
{
++Pi;
}
else if(C[B[i]-'a'])
{
C[B[i]-'a']--;
}
else
{
return 0;
}
}
return 1;
}
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&n);
scanf("%s",A+1);
scanf("%s",B+1);
int l=0;
int r=n;
int Key=-1;
while(l<=r)
{
int mid=(l+r)>>1;
if(check(mid))
{
r=mid-1;
Key=mid;
}
else
{
l=mid+1;
}
}
printf("%d",Key);
return 0;
}
C
成纸张了/kk
感觉像是什么建图然后钦定跑个基环树
结果实际上,如果把\(A\)相邻值相同的缩成一个块,可以发现操作实际上就是块之间的相互侵蚀
但不管怎么弄,相对顺序是不会变的,因此可以直接判断\(B\)缩块后是否是\(A\)的子序列
注意特判一下\(A\)弄不出来的情况
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=5005;
int T;
int n;
int A[MAXN];
int B[MAXN];
int Ta[MAXN];
int Tb[MAXN];
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&T);
for(int id=1;id<=T;id++)
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&A[i]);
}
int Cnx=0;
Ta[++Cnx]=A[1];
int Last=A[1];
for(int i=2;i<=n;i++)
{
if(A[i]==Last)
{
}
else
{
Ta[++Cnx]=A[i];
Last=A[i];
}
}
if(Ta[Cnx]==Ta[1]&&Cnx!=1)
{
Cnx--;
}
for(int i=1;i<=n;i++)
{
scanf("%d",&B[i]);
}
int Ca=Cnx;
Cnx=0;
Tb[++Cnx]=B[1];
Last=B[1];
for(int i=2;i<=n;i++)
{
if(B[i]==Last)
{
}
else
{
Tb[++Cnx]=B[i];
Last=B[i];
}
}
if(Tb[Cnx]==Tb[1]&&Cnx!=1)
{
Cnx--;
}
int Cb=Cnx;
if(Ca==Cb&&Ca==n)
{
bool fp=1;
for(int i=1;i<=Ca;i++)
{
if(Ta[i]!=Tb[i])
{
fp=0;
}
}
if(fp)
{
printf("Yes\n");
}
else
{
printf("No\n");
}
continue;
}
bool f=0;
for(int i=1;i<=Ca;i++)
{
int Pi=1;
for(int j=i;j<=Ca;j++)
{
if(Pi<=Cb&&Ta[j]==Tb[Pi])
{
++Pi;
}
}
for(int j=1;j<i;j++)
{
if(Pi<=Cb&&Ta[j]==Tb[Pi])
{
++Pi;
}
}
if(Pi==Cb+1)
{
f=1;
}
}
if(f)
{
printf("Yes\n");
}
else
{
printf("No\n");
}
}
return 0;
}
D
先找\(1\),只要\(2P_i>P_j\)返回\(No\)说明\(i\)可能成为\(1\),直接顺着做即可,会用\(N\)次操作
找到\(1\)后,\(P_i+1>P_j\)返回\(No\)直接说明\(P_i<P_j\),因此我们可以比较两数大小
直接归并即可
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=2005;
int n;
int P[MAXN];
int Tmp[MAXN];
string S;
int P1=1;
bool cmp(int x,int y)
{
cout<<'?'<<' '<<x<<' '<<P1<<' '<<y<<endl;
cin>>S;
if(S[0]=='N')
{
return 0;
}
return 1;
}
void solve(int l,int r)
{
if(l>r)
{
return;
}
if(l==r)
{
return;
}//3 1 2 4
int mid=(l+r)>>1;
solve(l,mid);
solve(mid+1,r);
int pi=l;
int pj=mid+1;
int pt=l;
while(pi<=mid&&pj<=r)
{
if(!cmp(P[pi],P[pj]))
{
Tmp[pt++]=P[pi++];
}
else
{
Tmp[pt++]=P[pj++];
}
}
while(pi<=mid)
{
Tmp[pt++]=P[pi++];
}
while(pj<=r)
{
Tmp[pt++]=P[pj++];
}
for(int i=l;i<=r;i++)
{
P[i]=Tmp[i];
}
}
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
cin>>n;
for(int i=2;i<=n;i++)
{
cout<<'?'<<' '<<i<<' '<<i<<' '<<P1<<endl;
cin>>S;
if(S[0]=='N')
{
P1=i;
}
}
for(int i=1;i<=n;i++)
{
P[i]=i;
}
solve(1,n);
for(int i=1;i<=n;i++)
{
Tmp[P[i]]=i;
}
cout<<'!';
for(int i=1;i<=n;i++)
{
cout<<' '<<Tmp[i];
}
cout<<endl;
return 0;
}
E
神仙题
首先考虑\(f(P)\)是什么
考虑拆开每个\(i\)的贡献\(f(P)=\sum\limits_{i=1}i(\sum\limits_{j<i}[P_i<P_j]-\sum\limits_{j>i}[P_j<P_i])\)
注意到
\(\sum\limits_{j<i}[P_i<P_j]+\sum\limits_{j<i}[P_i>P_j]=i-1\)
\(\sum\limits_{j<i}[P_i>P_j]+\sum\limits_{j>i}[P_i>P_j]=P_i-1\)
两式相减就是上面括号里面的式子
即\(\sum\limits_{i=1}i(i-P_i)\)
有\(m\)次操作这玩意直接求并不好做,我们考虑求个期望
问题在于求\(E(\sum\limits iP_i)\)
也即\(\sum\limits E(i)P_i\)
然后你会发现,如果有操作作用到\(i\)上,考虑走到\(j\)
其满足的方案数为\(min(i,n-i+1,j,n-j+1)\),那其实走到\(n-j+1\)的概率和走到\(j\)的概率是一样的,那\(j,n-j+1\)对期望的贡献就是\(P(j)\dfrac{n+1}{2}\)
因此\(E(i)\)决定于\(i\)是否会被操作,这个直接算就行了
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MOD=998244353;
const int MAXN=2e5+5;
int Pow(int a,int b,int p)
{
int res=1;
int base=a;
while(b)
{
if(b&1)
{
res=((long long)res*base)%p;
}
base=((long long)base*base)%p;
b>>=1;
}
return res;
}
int inv(int a,int p)
{
return Pow(a,p-2,p);
}
int n,m;
int P[MAXN];
int inv2;
int C(int n)
{
return ((((long long)n*(n+1))%MOD)*inv2)%MOD;
}
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d %d",&n,&m);
inv2=MOD-MOD/2;
int Res=0;
for(int i=1;i<=n;i++)
{
scanf("%d",&P[i]);
Res=((long long)Res+((long long)i*i)%MOD)%MOD;
}
for(int i=1;i<=n;i++)
{
int p=((((long long)C(i-1)+C(n-i))%MOD)*(inv(C(n),MOD)))%MOD;
int Rp=((long long)Pow(p,m,MOD)*i)%MOD;
int Rq=(((long long)(1ll-Pow(p,m,MOD)+MOD)%MOD)*((((long long)n+1)*inv2)%MOD))%MOD;
Rp=((long long)Rp+Rq)%MOD;
//printf("%d %d %d???\n",p,i,Rp);
Rp=((long long)Rp*P[i])%MOD;
Res=((long long)Res-Rp+MOD)%MOD;
}
Res=((long long)Res*Pow(C(n),m,MOD))%MOD;
printf("%d",Res);
return 0;
}
ARC164
究极下饭场/kk
A
考虑先给\(N\)按三进制分解一下
然后对于\(3^m\rightarrow3^{m-1}\),实际上可以加\(2\)的贡献,我们先计算\(N\)最小需要\(S\)
然后可以发现只要\(K-S\)是偶数即可
Show Code
#include<bits/stdc++.h>
using namespace std;
signed main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
int T;
long long N,K;
scanf("%d",&T);
while(T--)
{
scanf("%lld %lld",&N,&K);
if((N-K)&1)
{
printf("No\n");
continue;
}
long long Now=N;
long long S=0;
while(Now)
{
S+=(Now%3);
Now/=3;
// cerr<<Now<<endl;
}
if((S<=K)&&(K-S)%2==0)
{
printf("Yes\n");
}
else
{
printf("No\n");
}
}
}
B
就是找\(01\)交替然后只有一条相同边的奇环
好像不能直接找环,因为环套环会出问题
直接由并查集维护即可,颜色不同的连边
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=3e5+5;
int n,m;
int x,y;
struct Edge{
int u,v;
}edge[MAXN];
int fa[MAXN];
int c[MAXN];
int find(int x)
{
if(fa[x]==x)
{
return fa[x];
}
fa[x]=find(fa[x]);
return fa[x];
}
void unionn(int i,int j)
{
fa[find(i)]=find(j);
}
bool found=0;
int main(){
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d %d",&n,&m);
for(int i=1;i<=m;i++)
{
scanf("%d %d",&x,&y);
edge[i].u=x;
edge[i].v=y;
}
for(int i=1;i<=n;i++)
{
scanf("%d",&c[i]);
fa[i]=i;
}
for(int i=1;i<=m;i++)
{
if(c[edge[i].u]!=c[edge[i].v])
{
unionn(edge[i].u,edge[i].v);
}
}
for(int i=1;i<=m;i++)
{
if(c[edge[i].u]==c[edge[i].v])
{
if(find(edge[i].u)==find(edge[i].v))
{
found=1;
}
}
}
if(found)
{
printf("Yes");
}
else
{
printf("No");
}
}
C
先假设全部是\(A\)朝上
对于\(A\)来说,翻肯定选\(B_i-A_i\)最大的
对于\(B\),同样也要这样选
由于\(A\)一定会翻\(n\)次,这里我们可以用堆模拟这个过程,注意\(A\)可以反悔
Show Code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN=3e5+5;
int n;
struct node{
int A,B;
}s[MAXN];
signed main(){
freopen("date.in","r",stdin);
freopen("date.out","w",stdout);
scanf("%lld",&n);
int Sum=0;
priority_queue<int>Q;
for(int i=1;i<=n;i++)
{
scanf("%lld %lld",&s[i].A,&s[i].B);
Sum+=s[i].A;
Q.push(-(s[i].B-s[i].A));
}
int Op=0;
while(Q.size())
{
int temp=Q.top();
Q.pop();
if(!Op)
{
Sum-=temp;
Q.push(-temp);
}
// printf("%d %d??\n",temp,Op);
Op^=1;
}
printf("%lld",Sum);
}
D
如果能确定每个点的走的朝向,那其实可以直接抽象为括号匹配,答案就是每对匹配括号的距离之和
一个经典的套路,我们可以把左括号的贡献定义为\(-i\),这样我们就只需要算其合法序列的个数
考虑枚举位置\(i\)前面的\(?\)是\(+\)的数量,然后\(i\)的朝向就确定了,直接组合数算贡献即可
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MOD=998244353;
const int MAXN=3005;
int n;
char s[MAXN*2];
int dp[MAXN*2][MAXN*2];
int Pow(int a,int b,int p)
{
int res=1;
int base=a;
while(b)
{
if(b&1)
{
res=((long long)res*base)%p;
}
base=((long long)base*base)%p;
b>>=1;
}
return res;
}
int inv(int a,int p)
{
return Pow(a,p-2,p);
}
int fac[MAXN*2];
int inv_fac[MAXN*2];
int C(int n,int m)
{
if(n<m||m<0)
{
return 0;
}
if((n==m)||(m==0))
{
return 1;
}
return ((((long long)fac[n]*inv_fac[m])%MOD)*inv_fac[n-m])%MOD;
}
int Prel[MAXN*2];
int Prer[MAXN*2];
int Surl[MAXN*2];
int Surr[MAXN*2];
int Prep[MAXN*2];
int Surp[MAXN*2];
signed main(){
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&n);
scanf("%s",s+1);
fac[0]=1;
for(int i=1;i<=2*n;i++)
{
fac[i]=((long long)fac[i-1]*i)%MOD;
}
inv_fac[2*n]=inv(fac[2*n],MOD);
for(int i=2*n-1;i>=1;i--)
{
inv_fac[i]=((long long)inv_fac[i+1]*(i+1))%MOD;
}
int Res=0;
int Tot=0;
int Totl=0;
int Totr=0;
for(int i=1;i<=2*n;i++)
{
Prel[i]=Prel[i-1];
Prer[i]=Prer[i-1];
Prep[i]=Prep[i-1];
if(s[i]=='+')
{
Prel[i]++;
Totl++;
}
else if(s[i]=='-')
{
Prer[i]++;
Totr++;
}
else
{
Prep[i]++;
Tot++;
}
}
for(int i=2*n;i>=1;i--)
{
Surl[i]=Surl[i+1];
Surr[i]=Surr[i+1];
Surp[i]=Surp[i+1];
if(s[i]=='+')
{
Surl[i]++;
}
else if(s[i]=='-')
{
Surr[i]++;
}
else
{
Surp[i]++;
}
}
for(int i=1;i<=2*n;i++)
{
if(s[i]!='+')
{
int O1=Prel[i-1];
int O2=Prer[i-1];
int O3=Surl[i+1];
int O4=Surr[i+1];
int O5=Prep[i-1];
int O6=Surp[i+1];
int O=O4-O3+O1-O2;
for(int j=0;j<=O5;j++)
{
int Tp=(Totl+j);
int Np=(n-Tp);
if(Np>=0)
{
if(O+j-(O5-j)-Np+(O6-Np)<0)
{
int Tx=((long long)C(O5,j)*C(O6,Np))%MOD;
Tx=((long long)Tx*(MOD-i))%MOD;
// printf("%d -%d %d %d %d %d??\n",i,(MOD-Tx)%MOD,O5,O6,j,Np);
Res=((long long)Res+Tx)%MOD;
}
else
{
int Tx=((long long)C(O5,j)*C(O6,Np))%MOD;
Tx=((long long)Tx*(i))%MOD;
// printf("%d %d>??\n",i,Tx);
Res=((long long)Res+Tx)%MOD;
}
}
}
}
if(s[i]!='-')
{
int O1=Prel[i-1];
int O2=Prer[i-1];
int O3=Surl[i+1];
int O4=Surr[i+1];
int O5=Prep[i-1];
int O6=Surp[i+1];
int O=O4-O3+O1-O2;
for(int j=0;j<=O5;j++)
{
int Tp=(Totl+j);
if(s[i]=='?')
{
Tp++;
}
int Np=(n-Tp);
if(Np>=0)
{
if(O+j-(O5-j)-Np+(O6-Np)>0)
{
int Tx=((long long)C(O5,j)*C(O6,Np))%MOD;
Tx=((long long)Tx*(MOD-i))%MOD;
// printf("%d -%d??\n",i,(MOD-Tx)%MOD);
Res=((long long)Res+Tx)%MOD;
}
else
{
int Tx=((long long)C(O5,j)*C(O6,Np))%MOD;
Tx=((long long)Tx*(i))%MOD;
// printf("%d %d>??\n",i,Tx);
Res=((long long)Res+Tx)%MOD;
}
}
}
}
}
printf("%d\n",Res);
}
E
对于每个线段树的结点\(i\),我们记录分割点\(P_i\)
可以发现,对于区间\([l,r]\),它询问到的最大深度就是\(l-1,r\)分割点对应的节点的最大深度,因为对于中间的那段区间实际上一定是在其上面覆盖的
对于第一问,我们可以计算需要哪些分割点,然后在二叉树上一层一层铺即可
对于第二问,可以发现如果如果我们的分割点在\(d-1\),那访问次数实际上为在\(d-1\)深度分割点的数量\(\times2\)
于是我们要让位于\(d-1\)的分割点尽量少
对于\(d-1\)的一颗满二叉树,我们可以发现如果以\(dfs\)序标号,\(d-1\)的点都是奇数
据此我们可以\(dp\),设\(dp_{i,j}\)为前\(i\)需要的分割点走了\(j\)个点的最小次数,奇数位置放要记录贡献,偶数不用
Show Code
#include<bits/stdc++.h>
using namespace std;
int n,Q;
int l,r;
int C[5005];
vector<int>V;
int dp[5005][5005];
signed main(){
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d %d",&n,&Q);
for(int i=1;i<=Q;i++)
{
scanf("%d %d",&l,&r);
C[l-1]++;
C[r]++;
}
int d=0;
V.clear();
for(int i=1;i<n;i++)
{
if(C[i])
{
V.push_back(C[i]);
}
}
for(int i=0;i<=20;i++)
{
if(((1<<i)-1)>=((int)V.size()))
{
d=i;
break;
}
}
if(d==0)
{
printf("%d %d\n",0,Q);
return 0;
}
memset(dp,0x3f,sizeof(dp));
dp[0][0]=0;
for(int i=0;i<V.size();i++)
{
for(int j=0;j<(1<<d);j++)
{
if((j%2==0))
{
dp[i+1][j+1]=min(dp[i+1][j+1],dp[i][j]+V[i]);
dp[i][j+1]=min(dp[i][j+1],dp[i][j]);
}
else
{
dp[i+1][j+1]=min(dp[i+1][j+1],dp[i][j]);
}
}
}
int Res=0x3f3f3f3f;
for(int i=0;i<(1<<d);i++)
{
Res=min(Res,dp[V.size()][i]);
}
//printf("%d %d???\n",V.size(),(1<<d)-1);
printf("%d %d\n",d,2*Res);
}
ARC165
A
猜的结论,质因数\(\ge2\)
感觉证明不难
Show Code
#include<bits/stdc++.h>
using namespace std;
int t;
int n;
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&t);
while(t--)
{
scanf("%d",&n);
int cnt_prime=0;
for(int i=2;i<=n/i;i++)
{
if(n%i==0)
{
++cnt_prime;
while(n%i==0)
{
n/=i;
}
}
}
if(n>1)
{
++cnt_prime;
}
if(cnt_prime>=2)
{
printf("Yes\n");
}
else
{
printf("No\n");
}
}
}
B
对于两段操作区间,我们比较是否更有关键在于第一个变动的位置
这启示我们维护一段区间最长的不变位置,注意到相同的变动位置操作的左区间小的优
这玩意直接滑动窗口+双指针维护就行了(虽然我是直接二分的
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=2e5+5;
int a[MAXN];
int n,k;
int dq[MAXN];
int head;
int tail;
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d %d",&n,&k);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
}
head=1;
tail=0;
int Maxi=0;
int Kt;
for(int i=1;i<=n;i++)
{
while(head<=tail&&i-dq[head]>=k)
{
head++;
}
while(head<=tail&&a[dq[tail]]>a[i])
{
tail--;
}
dq[++tail]=i;
if(i>=k)
{
int l=head;
int r=tail;
int Key=i-k;
while(l<=r)
{
int mid=(l+r)>>1;
if(dq[mid]-(i-k)==mid-head+1)
{
l=mid+1;
Key=dq[mid];
}
else
{
r=mid-1;
}
}
if(Key>Maxi)
{
Kt=i-k+1;
Maxi=Key;
}
if(Key==i)
{
for(int i=1;i<=n;i++)
{
printf("%d ",a[i]);
}
return 0;
}
}
}
sort(a+Kt,a+Kt+k);
//printf("%d\n",Kt);
for(int i=1;i<=n;i++)
{
printf("%d ",a[i]);
}
}
C
有点抽象,建议和\(B\)换个位置
可以发现\(X\)的上界由最多由两条边决定
直接二分+二分图判定即可
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=2e5+5;
struct Edge{
int v,val;
bool operator<(const Edge x)const{
return val<x.val;
}
};
int n,m;
int x,y,z;
vector<Edge>g[MAXN];
int col[MAXN];
bool found=0;
int Lit;
void dfs(int x,int c)
{
if(col[x])
{
if(col[x]!=c)
{
found=1;
}
return;
}
col[x]=c;
for(int i=0;i<g[x].size();i++)
{
int v=g[x][i].v;
int w=g[x][i].val;
if(w<Lit)
{
dfs(v,(c==1)?2:1);
}
}
}
bool check(int mid)
{
for(int i=1;i<=n;i++)
{
col[i]=0;
}
found=0;
Lit=mid;
for(int i=1;i<=n;i++)
{
if(!col[i])
{
dfs(i,1);
}
}
if(found)
{
return 0;
}
else
{
return 1;
}
}
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d %d",&n,&m);
for(int i=1;i<=m;i++)
{
scanf("%d %d %d",&x,&y,&z);
g[x].push_back((Edge){y,z});
g[y].push_back((Edge){x,z});
}
int Mini=2e9+1;
for(int i=1;i<=n;i++)
{
sort(g[i].begin(),g[i].end());
if(g[i].size()==1)
{
}
else
{
Mini=min(Mini,g[i][0].val+g[i][1].val);
}
}
int l=0;
int r=Mini;
int Key;
//cerr<<"fuck"<<endl;
while(l<=r)
{
//cerr<<l<<' '<<r<<endl;
int mid=((long long)l+r)>>1;
if(check(mid))
{
Key=mid;
l=mid+1;
}
else
{
r=mid-1;
}
}
printf("%d\n",Key);
}
D
智慧题
首先这玩意可以直接得到\([A,B]\),\([C,D]\)的偏序关系,如果我们先连\(A\rightarrow C\)表示\(A\le C\)
如果跑出来没环就说明合法,否则说明某些限制条件得往后考虑
直接跑\(tarjan\)即可,直到没有环
这里我们为了保证点数,跑出来的\(scc\)得用并查集连边
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=2005;
int n,m;
int l1[MAXN],l2[MAXN],r1[MAXN],r2[MAXN];
int P1[MAXN],P2[MAXN];
vector<int>g[MAXN];
int dfn[MAXN];
int low[MAXN];
int scc[MAXN];
int cnt_dfn;
int cnt_scc;
stack<int>st;
int vis[MAXN];
int fa[MAXN];
int find(int x)
{
if(fa[x]==x)
{
return fa[x];
}
fa[x]=find(fa[x]);
return fa[x];
}
void unionn(int i,int j)
{
fa[find(i)]=find(j);
}
void dfs(int x)
{
dfn[x]=++cnt_dfn;
low[x]=dfn[x];
st.push(x);
for(int i=0;i<g[x].size();i++)
{
int v=g[x][i];
if(dfn[v])
{
if(!scc[v])
{
low[x]=min(low[x],dfn[v]);
}
}
else
{
dfs(v);
low[x]=min(low[x],low[v]);
}
}
if(low[x]==dfn[x])
{
++cnt_scc;
while(st.size())
{
scc[st.top()]=cnt_scc;
if(st.top()==x)
{
st.pop();
break;
}
st.pop();
}
}
}
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d %d",&n,&m);
for(int i=1;i<=m;i++)
{
scanf("%d %d %d %d",&l1[i],&r1[i],&l2[i],&r2[i]);
P1[i]=l1[i];
P2[i]=l2[i];
}
for(int i=1;i<=n;i++)
{
fa[i]=i;
}
while(1)
{
for(int i=1;i<=n;i++)
{
g[i].clear();
dfn[i]=0;
low[i]=0;
scc[i]=0;
}
while(st.size())
{
st.pop();
}
cnt_dfn=cnt_scc=0;
for(int i=1;i<=m;i++)
{
if(!vis[i])
{
g[find(P1[i])].push_back(find(P2[i]));
}
}
for(int i=1;i<=n;i++)
{
if(!dfn[i])
{
dfs(i);
}
}
bool f=1;
for(int i=1;i<=m;i++)
{
if((!vis[i])&&scc[find(P1[i])]==scc[find(P2[i])])
{
f=0;
P1[i]++;
P2[i]++;
if(P1[i]>r1[i])
{
vis[i]=1;
}
if(P2[i]>r2[i])
{
printf("No\n");
return 0;
}
}
}
for(int i=1;i<=n;i++)
{
for(int j=0;j<g[i].size();j++)
{
int v=g[i][j];
if(scc[find(i)]==scc[find(v)])
{
unionn(i,v);
}
}
}
if(f)
{
break;
}
}
printf("Yes\n");
}
E
经典鞭尸题(虽然是搬运工
可以发现如果我们操作一些点数小于\(k\)的联通块实际上对最后的答案也没影响
然后还是经典的把贡献拆到每个点上,我们只需要计算\(u\)这个点产生有用断边的概率即可
然后接下来我们可以假装所有点都被操作一次,生成一个排列,依次操作,只有当\(u\)
操作时联通块\(\ge k\)时这个点可以产生贡献
根据这个我们可以设\(dp_{u,i,j}\)表示当前\(u\)及其子树内有\(i\)个点在\(u\)之前操作,当前有\(j\)个点与\(u\)联通的方案数
这玩意求得是子树内得贡献,多换几次根就行了
Show Code
// LUOGU_RID: 125255492
#include<bits/stdc++.h>
using namespace std;
const int MOD=998244353;
const int MAXN=105;
int Pow(int a,int b,int p)
{
int res=1;
int base=a;
while(b)
{
if(b&1)
{
res=((long long)res*base)%p;
}
base=((long long)base*base)%p;
b>>=1;
}
return res;
}
int inv(int a,int p)
{
return Pow(a,p-2,p);
}
int fac[MAXN];
int inv_fac[MAXN];
int C(int n,int m)
{
if(n<m||m<0)
{
return 0;
}
if(n==m||m==0)
{
return 1;
}
return ((((long long)fac[n]*inv_fac[m])%MOD)*inv_fac[n-m])%MOD;
}
int n,k;
int x,y;
vector<int>g[MAXN];
int dp[MAXN][MAXN][MAXN];
int Siz[MAXN];
int Tmp[MAXN][MAXN];
void dfs(int x,int f)
{
Siz[x]=1;
dp[x][0][0]=1;
for(int i=0;i<g[x].size();i++)
{
int v=g[x][i];
if(v==f)
{
continue;
}
dfs(v,x);
for(int p=0;p<=Siz[x]+Siz[v];p++)
{
for(int q=0;q<=Siz[x]+Siz[v];q++)
{
Tmp[p][q]=dp[x][p][q];
dp[x][p][q]=0;
}
}
for(int p1=0;p1<=Siz[x];p1++)
{
for(int q1=0;q1<=Siz[x];q1++)
{
for(int p2=0;p2<=Siz[v];p2++)
{
for(int q2=0;q2<=Siz[v];q2++)
{
dp[x][p1+p2][q1+q2]=((long long)dp[x][p1+p2][q1+q2]+((long long)Tmp[p1][q1]*dp[v][p2][q2]))%MOD;
}
}
}
}
Siz[x]+=Siz[v];
}
for(int i=1;i<=Siz[x];i++)
{
dp[x][i][Siz[x]]=((long long)dp[x][i][Siz[x]]+C(Siz[x]-1,i-1))%MOD;//为啥要减1??
}
}
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d %d",&n,&k);
for(int i=1;i<n;i++)
{
scanf("%d %d",&x,&y);
g[x].push_back(y);
g[y].push_back(x);
}
fac[0]=1;
inv_fac[0]=1;
for(int i=1;i<=n;i++)
{
fac[i]=((long long)fac[i-1]*i)%MOD;
inv_fac[i]=((long long)inv_fac[i-1]*inv(i,MOD))%MOD;
}
int Res=0;
for(int rt=1;rt<=n;rt++)
{
memset(dp,0,sizeof(dp));
dfs(rt,0);
for(int p=0;p<n;p++)
{
for(int q=0;q<=n;q++)
{
if(q>=n-k)
{
break;
}
int Nt=((long long)dp[rt][p][q]*fac[p])%MOD;
Nt=((long long)Nt*fac[n-1-p])%MOD;
Nt=((long long)Nt*inv_fac[n])%MOD;
Res=((long long)Res+Nt)%MOD;
}
}
}
printf("%d\n",Res);
}
F
不难观察出形似\(AABB,ABAB\),\(A,B\)之间的顺序是固定的
如果我们把一个数的出现位置\((l,r)\)放在坐标系上,可以发现就是向它的右上所有点连边
直接主席树优化建图跑拓扑即可
Show Code
#include<bits/stdc++.h>
#define ls Tree[p].lc
#define rs Tree[p].rc
using namespace std;
const int MAXN=5e5+5;
int n;
int a[MAXN*2];
struct node{
int l,r,u;
bool operator<(const node x)const{
return l>x.l;
}
}b[MAXN];
int las[MAXN];
vector<int>g[MAXN*100];
int cnt_id;
int rt[MAXN];
struct Seg{
int id;
int lc,rc;
}Tree[MAXN*100];
int cnt_node;
int Rd[MAXN*100];
int copy(int p)
{
Tree[++cnt_node]=Tree[p];
return cnt_node;
}
void Insert(int &p,int o,int l,int r,int k,int v)
{
p=copy(o);
Tree[p].id=++cnt_id;
if(l==r)
{
g[Tree[p].id].push_back(v);
// printf("%d %d\n",Tree[p].id,v);
Rd[v]++;
return;
}
int mid=(l+r)>>1;
if(k<=mid)
{
Insert(ls,Tree[o].lc,l,mid,k,v);
}
else
{
Insert(rs,Tree[o].rc,mid+1,r,k,v);
}
if(ls)
{
g[Tree[p].id].push_back(Tree[ls].id);
// printf("%d %d\n",Tree[p].id,Tree[ls].id);
Rd[Tree[ls].id]++;
}
if(rs)
{
g[Tree[p].id].push_back(Tree[rs].id);
// printf("%d %d\n",Tree[p].id,Tree[rs].id);
Rd[Tree[rs].id]++;
}
}
void Update(int p,int l,int r,int ql,int qr,int u)
{
if(!p)
{
return;
}
if(ql>qr)
{
return;
}
//printf("%d??\n",p);
if(l>=ql&&r<=qr)
{
//printf("fuckfuckf\n");
g[u].push_back(Tree[p].id);
//printf("%d %d\n",u,Tree[p].id);
Rd[Tree[p].id]++;
return;
}
int mid=(l+r)>>1;
if(ql<=mid)
{
Update(ls,l,mid,ql,qr,u);
}
if(qr>mid)
{
Update(rs,mid+1,r,ql,qr,u);
}
}
struct Node{
int u,val;
bool operator<(const Node x)const{
return val>x.val;
}
};
int Cal(int x)
{
if(x<=n)
{
return x;
}
else
{
return 0;
}
}
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&n);
int cnt=0;
for(int i=1;i<=(n<<1);i++)
{
scanf("%d",&a[i]);
if(las[a[i]])
{
b[++cnt]=(node){las[a[i]],i,a[i]};
}
else
{
las[a[i]]=i;
}
}
cnt_id=n;
sort(b+1,b+1+n);
for(int i=1;i<=n;i++)
{
//printf("%d???\n",b[i].u);
Insert(rt[i],rt[i-1],1,2*n,b[i].r,b[i].u);
Update(rt[i],1,2*n,b[i].r+1,2*n,b[i].u);
}
priority_queue<Node>Q;
for(int i=1;i<=cnt_id;i++)
{
if(!Rd[i])
{
Q.push((Node){i,Cal(i)});
//printf("%d----\n",i);
}
}
while(Q.size())
{
Node temp=Q.top();
Q.pop();
if(temp.u<=n)
{
printf("%d %d ",temp.u,temp.u);
}
for(int i=0;i<g[temp.u].size();i++)
{
int v=g[temp.u][i];
Rd[v]--;
if(!Rd[v])
{
Q.push((Node){v,Cal(v)});
}
}
}
}
ARC150
A
直接枚举对应区间即可
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=4e5+5;
int t;
int n,k;
char s[MAXN];
int sum1[MAXN];
int sum2[MAXN];
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&t);
while(t--)
{
scanf("%d %d",&n,&k);
scanf("%s",s+1);
for(int i=1;i<=n;i++)
{
sum1[i]=sum1[i-1]+(s[i]=='1');
sum2[i]=sum2[i-1]+(s[i]=='0');
}
int f=0;
for(int i=1;i<=n-k+1;i++)
{
int l=i;
int r=i+k-1;
if(sum1[r]-sum1[l-1]==sum1[n]&&(sum2[r]-sum2[l-1]==0))
{
f++;
}
}
if(f==1)
{
printf("Yes\n");
}
else
{
printf("No\n");
}
}
}
B
猜的结论,枚举\(X\)在\(1e5\)的范围内,\(Y\)在\(100\)的范围
正解也差不不多,根据\(k(A+X)=B+Y\)根号分治
Show Code
#include<bits/stdc++.h>
#define int long long
using namespace std;
int t,A,B;
signed main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%lld",&t);
while(t--)
{
scanf("%lld %lld",&A,&B);
int Res=2e18;
for(int X=0;X<=100000;X++)
{
int Te=(X+A);
int Y=(Te-(B%Te))%Te;
Res=min(Res,X+Y);
}
for(int Y=0;Y<=100;Y++)
{
int Te=Y+B;
for(int i=1;i<=Te/i;i++)
{
if(Te%i==0)
{
if(i>=A)
{
Res=min(Res,i-A+Y);
}
if((Te/i)>=A)
{
Res=min(Res,(Te/i)-A+Y);
}
}
}
}
printf("%lld\n",Res);
}
}
C
题看错做了半天/kk
注意是最小,最短路转移没后效性,直接用即可
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=1e5+5;
int n,m;
int A[MAXN];
int x,y;
vector<int>g[MAXN];
int K;
int B[MAXN];
int vis[MAXN];
int dp[MAXN];
struct node{
int u,val;
bool operator<(const node x)const{
return val>x.val;
}
};
void dijkstra(int s)
{
memset(vis,0,sizeof(vis));
memset(dp,0x3f,sizeof(dp));
dp[s]=(B[1]==A[s]);
priority_queue<node>q;
q.push((node){s,dp[s]});
while(q.size())
{
node temp=q.top();
q.pop();
if(vis[temp.u])
{
continue;
}
vis[temp.u]=1;
for(int i=0;i<g[temp.u].size();i++)
{
int v=g[temp.u][i];
if(dp[v]>dp[temp.u]+(A[v]==B[dp[temp.u]+1]))
{
dp[v]=dp[temp.u]+(A[v]==B[dp[temp.u]+1]);
q.push((node){v,dp[v]});
}
}
}
}
signed main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d %d %d",&n,&m,&K);
for(int i=1;i<=m;i++)
{
scanf("%d %d",&x,&y);
g[x].push_back(y);
g[y].push_back(x);
}
for(int i=1;i<=n;i++)
{
scanf("%d",&A[i]);
}
for(int i=1;i<=K;i++)
{
scanf("%d",&B[i]);
}
dijkstra(1);
// for(int i=1;i<=n;i++)
// {
// printf("%d\n",dp[i]);
// }
if(dp[n]==K)
{
printf("Yes\n");
}
else
{
printf("No\n");
}
}
D
经典拆贡献到每个点上
鞭尸没影响,所以如果可以重复操作一个点
可以发现一个点被选中的次数是关于它的深度的,这个问题等价于考虑它和它的祖先,每个点选的概率是等价的,每个点都被选中后停止,要求得末端点被选中的次数
考虑当前选中的点有\(k\)个,深度为\(d\),那么选中没选点的概率是\(\dfrac{d-k}{d}\)
那么选到的期望次数是\(\dfrac{d}{d-k}\),我们选完的期望次数为\(d\sum\limits_{k=1}^{d}\dfrac{1}{k}\),选到\(x\)的次数为\(\sum\limits_{k=1}^{d}\dfrac{1}{k}\)
加起来即可
Show Code
// LUOGU_RID: 125247122
#include<bits/stdc++.h>
using namespace std;
const int MOD=998244353;
const int MAXN=2e5+5;
int Pow(int a,int b,int p)
{
int res=1;
int base=a;
while(b)
{
if(b&1)
{
res=((long long)res*base)%p;
}
base=((long long)base*base)%p;
b>>=1;
}
return res;
}
int inv(int a,int p)
{
return Pow(a,p-2,p);
}
int n;
int p;
vector<int>g[MAXN];
int dep[MAXN];
void dfs(int x)
{
for(int i=0;i<g[x].size();i++)
{
int v=g[x][i];
dep[v]=dep[x]+1;
dfs(v);
}
}
int F[MAXN];
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
F[i]=((long long)F[i-1]+inv(i,MOD))%MOD;
}
for(int i=2;i<=n;i++)
{
scanf("%d",&p);
g[p].push_back(i);
}
dep[1]=1;
dfs(1);
int Res=0;
for(int i=1;i<=n;i++)
{
Res=((long long)Res+F[dep[i]])%MOD;
}
printf("%d\n",Res);
}
E
神秘提
被LYDD博傻了
首先第一步转化就没看出来/kk
把序列打到网格图,\(R\)往上走,\(L\)往下走,你会发现对于$L,f_i\ge0 \(的要翻折,\)R,f_i\ge f_n\(的要翻折,这里\)f_n\(表示第\)n\(个点停下来的\)y\(坐标,这里要求\)f_{nk}>0$
然后你会发现翻折一次后\(f_n\)就成最大值了,接下来的翻折所有\(\ge0\)的\(L\)都会翻折且因为向上翻所以只会翻一次,注意哪些从\(R\rightarrow L\rightarrow R\)的点,注意就算第一次翻下去了耶一定会经过一些操作返回来
而所有\(\ge0\)的\(L\)实际上在第一次也会被统计到,所以直接统计原序列里\(\ge 0\)的\(L\)和\(f_i\ge f_n\)的\(R\)即可
这里还循环了\(k\)次,注意循环一次之后就\(\ge 0\)了
Show Code
#include<bits/stdc++.h>
using namespace std;
#define sum 😂
const int MAXN=2e5+5;
const int MOD=998244353;
int n,k;
char s[MAXN];
int a[MAXN];
int sum[MAXN];
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d %d",&n,&k);
scanf("%s",s+1);
for(int i=1;i<=n;i++)
{
if(s[i]=='L')
{
a[i]=-1;
}
else
{
a[i]=1;
}
sum[i]=sum[i-1]+a[i];
}
if(sum[n]<0)
{
reverse(a+1,a+1+n);
for(int i=1;i<=n;i++)
{
a[i]=-a[i];
}
}
for(int i=1;i<=n;i++)
{
sum[i]=sum[i-1]+a[i];
}
int Res=0;
int Pos=n+1;
for(int i=1;i<=n;i++)
{
if(sum[i]>0)
{
Pos=i;
break;
}
}
if(sum[n]==0)
{
for(int i=1;i<=n;i++)
{
if(a[i]==1&&sum[i]>0)
{
Res=((long long)Res+k)%MOD;
}
else if(a[i]==-1&&sum[i]>=0)
{
Res=((long long)Res+k)%MOD;
}
}
printf("%d\n",Res);
return 0;
}
// for(int i=1;i<=n;i++)
// {
// printf("%d ",a[i]);
// }
// printf("\n");
for(int i=1;i<=n;i++)
{
if(a[i]==1)
{
int Times=max(0ll,k-max((((long long)k*sum[n]-sum[i])/(sum[n]))+1,0ll));
Res=((long long)Res+(2ll*Times)%MOD)%MOD;
}
else
{
Res=((long long)Res+k)%MOD;
}
}
for(int i=1;i<=Pos;i++)
{
if(a[i]==1)
{
}
else
{
Res=((long long)Res-1+MOD)%MOD;
}
}
printf("%d\n",Res);
}
ARC148
A
\(\bmod 2\)一定有\(1\)或\(2\),判一下\(1\)即可
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=5e5+5;
int n;
int a[MAXN];
int gcd(int a,int b)
{
if(!b)
{
return a;
}
else
{
return gcd(b,a%b);
}
}
int dc=1;
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
if(a[i]%2==0)
{
dc=0;
}
}
sort(a+1,a+1+n);
int g=0;
for(int i=2;i<=n;i++)
{
g=gcd(g,a[i]-a[i-1]);
}
if(g==1)
{
if(dc)
{
printf("1");
return 0;
}
printf("2");
}
else
{
printf("1");
}
}
B
模拟?
Show Code
#include<bits/stdc++.h>
using namespace std;
string s;
int n;
int main()
{
scanf("%d",&n);
cin>>s;
int Key=-1;
for(int i=0;i<n;i++)
{
if(s[i]=='p')
{
Key=i;
break;
}
}
if(Key==-1)
{
cout<<s;
}
else
{
// int Maxi=0;
// int Sum=0;
// int Kx;
// for(int i=Key;i<n;i++)
// {
// if(s[i]=='d')
// {
// Sum=0;
// }
// else
// {
// Sum++;
// if(Sum>Maxi)
// {
// Maxi=Sum;
// Kx=i;
// }
// }
// }
// for(int i=0;i<Key;i++)
// {
// printf("%c",s[i]);
// }
// for(int i=Kx;i>=Key;i--)
// {
// if(s[i]=='d')
// {
// printf("p");
// }
// else
// {
// printf("d");
// }
// }
// for(int i=Kx+1;i<n;i++)
// {
// printf("%c",s[i]);
// }
string Ans=s;
for(int i=Key;i<n;i++)
{
string sxv;
for(int j=0;j<Key;j++)
{
sxv+=s[j];
}
for(int j=i;j>=Key;j--)
{
if(s[j]=='p')
{
sxv+='d';
}
else
{
sxv+='p';
}
}
for(int j=i+1;j<n;j++)
{
sxv+=s[j];
}
Ans=min(Ans,sxv);
}
cout<<Ans;
}
}
C
模拟???
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=2e5+5;
int n;
int q;
int p[MAXN];
int M;
int S[MAXN];
int D[MAXN];
int Vis[MAXN];
int main()
{
scanf("%d %d",&n,&q);
for(int i=2;i<=n;i++)
{
scanf("%d",&p[i]);
D[p[i]]++;
}
while(q--)
{
scanf("%d",&M);
for(int i=1;i<=M;i++)
{
scanf("%d",&S[i]);
Vis[S[i]]=1;
}
int Ans=0;
for(int i=1;i<=M;i++)
{
if(Vis[p[S[i]]])
{
Ans+=D[S[i]]-1;
}
else
{
Ans+=1+D[S[i]];
}
}
printf("%d\n",Ans);
for(int i=1;i<=M;i++)
{
Vis[S[i]]=0;
}
}
}
D
有意思的博弈
如果最后剩下\(a,b\),已经有\(x,y\)了,如果\(B\)能赢,很明显要么\(a=b\),要么
\(x+a\equiv y+b(\bmod m)\)且\(y+a\equiv x+b(\bmod m)\),即\(a\equiv b+\dfrac{m}{2}(\bmod m)\)
我们先凑\(a=b\),再凑\(a\equiv b+\dfrac{m}{2}(\bmod m)\),如果能凑完且第二种的对数是偶数则\(B\)赢
显然这情况\(B\)能赢,对于不是的,\(A\)先选第二种对的一个数,然后\(A\)就模仿\(B\),到最后剩两个数一定也凑不出来
Show Code
#include<bits/stdc++.h>
using namespace std;
int n,m;
int x;
map<int,int>vis,tis;
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d %d",&n,&m);
for(int i=1;i<=2*n;i++)
{
scanf("%d",&x);
vis[x]++;
vis[x]%=2;
//printf("%d???\n",vis[1]);
}
for(auto it=vis.begin();it!=vis.end();it++)
{
pair<int,int>tp=(*it);
if(tp.second)
{
//printf("%d???\n",tp.second);
if(m&1)
{
printf("Alice");
return 0;
}
if(tp.first>=(m/2))
{
tis[tp.first-(m/2)]++;
}
else
{
tis[tp.first]++;
}
}
}
int Cnt=0;
for(auto it=tis.begin();it!=tis.end();it++)
{
pair<int,int>tp=(*it);
if(tp.second&1)
{
printf("Alice");
return 0;
}
else
{
Cnt+=(tp.second/2);
}
}
if(Cnt&1)
{
printf("Alice");
}
else
{
printf("Bob");
}
}
E
好巧
首先加一个\(1e9\)把问题转化为圆排列
这样两边得也有两个相邻
然后分割成\(<\dfrac{k}{2}\)得和\(\ge\)的,然后你会发现每个\(<\)的都要两个\(\ge\)的
然后绑在一起把它看成\(\ge\)的,我们只用从大到小处理即可
细节较多
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MOD=998244353;
const int MAXN=2e5+5;
int fac[MAXN];
int Pow(int a,int b,int p)
{
int res=1;
int base=a;
while(b)
{
if(b&1)
{
res=((long long)res*base)%p;
}
base=((long long)base*base)%p;
b>>=1;
}
return res;
}
int inv(int a,int p)
{
return Pow(a,p-2,p);
}
int n,k;
int x;
vector<int>s,t;
int cmp(int x,int y)
{
return x>y;
}
map<int,int>vis;
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d %d",&n,&k);
int Crp=0;
fac[0]=1;
for(int i=1;i<=n;i++)
{
fac[i]=((long long)fac[i-1]*i)%MOD;
scanf("%d",&x);
vis[x]++;
if(x>=(k+1)/2)
{
s.push_back(x);
Crp++;
}
else
{
t.push_back(x);
Crp--;
}
}
//printf("%d?\n",Crp);
if(Crp<-1)
{
printf("0");
return 0;
}
s.push_back(1e9);
sort(s.begin(),s.end());
sort(t.begin(),t.end());
int Res=1;
for(auto it=vis.begin();it!=vis.end();it++)
{
Res=((long long)Res*inv(fac[(*it).second],MOD))%MOD;
}
for(int i=0;i<t.size();i++)
{
int Cp=(s.size())-(lower_bound(s.begin(),s.end(),k-t[i])-s.begin()+1)+1;
// printf("%d %d??\n",i,Cp);
if((i==t.size()-1)&&(n+1==2*t.size()))
{
//printf("%d??\n",i);
continue;
}
if(Cp-i<2)
{
printf("0");
return 0;
}
Res=((long long)Res*(((long long)(Cp-i)*((Cp-i)-1))%MOD))%MOD;
}
for(int i=Crp;i>=1;i--)
{
Res=((long long)Res*i)%MOD;
}
printf("%d\n",Res);
}
ARC166
被\(A\)搞心态了/kk
A
按\(C\)分割后\(B\)可以左移,直接判就行了(虽然我写了5k+
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=2e5+5;
int t;
int n;
string S,T;
int M[MAXN];
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&t);
while(t--)
{
scanf("%d",&n);
cin>>S;
cin>>T;
bool f=1;
int las=0;
for(int i=0;i<=n;i++)
{
if(i==n)
{
int CntA=0,CntB=0;
for(int j=las;j<i;j++)
{
if(T[j]=='A')
{
CntA++;
}
else
{
CntB++;
}
}
for(int j=las;j<i;j++)
{
if(S[j]=='A')
{
CntA--;
}
else if(S[j]=='B')
{
CntB--;
}
}
for(int j=las;j<i;j++)
{
if(S[j]=='C')
{
if(CntA)
{
S[j]='A';
CntA--;
}
else
{
S[j]='B';
CntB--;
}
}
}
if((CntA!=0)||(CntB!=0))
{
f=0;
}
int Cnt=0;
int Now=0;
for(int j=i-1;j>=las;j--)
{
if(S[j]=='A')
{
++Now;
}
else
{
M[++Cnt]=Now;
}
}
Now=0;
Cnt=0;
for(int j=i-1;j>=las;j--)
{
if(T[j]=='A')
{
++Now;
}
else
{
++Cnt;
if(Now<M[Cnt])
{
f=0;
// printf("??");
}
}
}
las=i+1;
break;
}
if(T[i]=='C')
{
if(S[i]!='C')
{
f=0;
}
int CntA=0,CntB=0;
for(int j=las;j<i;j++)
{
if(T[j]=='A')
{
CntA++;
}
else
{
CntB++;
}
}
for(int j=las;j<i;j++)
{
if(S[j]=='A')
{
CntA--;
}
else if(S[j]=='B')
{
CntB--;
}
}
for(int j=las;j<i;j++)
{
if(S[j]=='C')
{
if(CntA)
{
S[j]='A';
CntA--;
}
else
{
S[j]='B';
CntB--;
}
}
}
if((CntA!=0)||(CntB!=0))
{
f=0;
//printf("%d %d\n",CntA,CntB);
}
int Cnt=0;
int Now=0;
for(int j=i-1;j>=las;j--)
{
if(S[j]=='A')
{
++Now;
}
else
{
M[++Cnt]=Now;
}
}
Now=0;
Cnt=0;
for(int j=i-1;j>=las;j--)
{
if(T[j]=='A')
{
++Now;
}
else
{
++Cnt;
if(Now<M[Cnt])
{
f=0;
//printf("??");
}
}
}
las=i+1;
}
}
if(f)
{
printf("Yes\n");
}
else
{
printf("No\n");
}
}
}
B
分讨一下是\(A,B,C\)还是\(A,lcm(B,C)\)还是\(lcm(A,B,C)\)即可
Show Code
#include<bits/stdc++.h>
#define int __int128
using namespace std;
void read(__int128 &x) {
x = 0;
int f = 1;
char s = getchar();
while (s > '9' || s < '0') {
if (s == '-')
f = -1;
s = getchar();
}
while (s >= '0' && s <= '9') {
x = (x << 3) + (x << 1) + (s - '0');
s = getchar();
}
x *= f;
}
void write(__int128 x) {
if (x < 0) {
putchar('-');
x = (~x) + 1;
}
if (x > 9) {
write(x / 10);
}
putchar(x % 10 + '0');
}
const int MAXN=2e5+5;
int n,a,b,c;
int s[MAXN];
int A[MAXN];
int B[MAXN];
int C[MAXN];
int lcm(int a,int b)
{
return a/__gcd(a,b)*b;
}
signed main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
read(n);
read(a);
read(b);
read(c);
set<pair<int,int> >Sa,Sb,Sc;
int Res=1e19;
for(int i=1;i<=n;i++)
{
read(s[i]);
A[i]=(a-s[i]%a)%a;
B[i]=(b-s[i]%b)%b;
C[i]=(c-s[i]%c)%c;
Sa.insert(make_pair(A[i],i));
Sb.insert(make_pair(B[i],i));
Sc.insert(make_pair(C[i],i));
Res=min(Res,(lcm(lcm(a,b),c)-s[i]%lcm(lcm(a,b),c))%lcm(lcm(a,b),c));
}
if(n>=3)
{
for(int i=1;i<=n;i++)
{
Sb.erase(make_pair(B[i],i));
Sc.erase(make_pair(C[i],i));
auto it=Sb.begin();
int j=(*it).second;
Sc.erase(make_pair(C[j],j));
auto jt=Sc.begin();
Res=min(Res,A[i]+(*it).first+(*jt).first);
Sc.insert(make_pair(C[j],j));
it=Sc.begin();
j=(*it).second;
Sb.erase(make_pair(B[j],j));
jt=Sb.begin();
Res=min(Res,A[i]+(*it).first+(*jt).first);
Sb.insert(make_pair(B[j],j));
Sb.insert(make_pair(B[i],i));
Sc.insert(make_pair(C[i],i));
}
}
if(n>=2)
{
for(int i=1;i<=n;i++)
{
Sc.erase(make_pair(C[i],i));
auto it=Sc.begin();
Res=min(Res,(lcm(a,b)-s[i]%lcm(a,b))%lcm(a,b)+(*it).first);
Sc.insert(make_pair(C[i],i));
}
for(int i=1;i<=n;i++)
{
Sb.erase(make_pair(B[i],i));
auto it=Sb.begin();
Res=min(Res,(lcm(a,c)-s[i]%lcm(a,c))%lcm(a,c)+(*it).first);
Sb.insert(make_pair(B[i],i));
}
for(int i=1;i<=n;i++)
{
Sa.erase(make_pair(A[i],i));
auto it=Sa.begin();
Res=min(Res,(lcm(b,c)-s[i]%lcm(b,c))%lcm(b,c)+(*it).first);
Sa.insert(make_pair(A[i],i));
}
}
write(Res);
}
C
把图画出来给每个格子建两个点,给对着隔一条边的点连边,得到\(min(n,m)+max(n,m)\)条链,你会发现限制就是这些链选点不相邻,预处理一下就好了
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MOD=998244353;
const int MAXN=4e6+5;
int Pow(int a,int b,int p)
{
int res=1;
int base=a;
while(b)
{
if(b&1)
{
res=((long long)res*base)%p;
}
base=((long long)base*base)%p;
b>>=1;
}
return res;
}
int inv(int a,int p)
{
return Pow(a,p-2,p);
}
int inv_fac[MAXN];
int fac[MAXN];
int C(int n,int m)
{
if(n<m||m<0)
{
return 0;
}
if(n==m||m==0)
{
return 1;
}
return ((((long long)fac[n]*inv_fac[m])%MOD)*inv_fac[n-m])%MOD;
}
int T,n,m;
int dp[MAXN][2];
int f[MAXN];
int g[MAXN];
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
fac[0]=1;
for(int i=1;i<=MAXN-5;i++)
{
fac[i]=((long long)fac[i-1]*i)%MOD;
}
inv_fac[MAXN-5]=inv(fac[MAXN-5],MOD);
for(int i=MAXN-5-1;i>=1;i--)
{
inv_fac[i]=((long long)inv_fac[i+1]*(i+1))%MOD;
}
dp[1][0]=dp[1][1]=1;
for(int i=2;i<=MAXN-5;i++)
{
dp[i][0]=((long long)dp[i-1][0]+dp[i-1][1])%MOD;
dp[i][1]=dp[i-1][0];
}
for(int i=1;i<=MAXN-5;i++)
{
f[i]=((long long)dp[i][0]+dp[i][1])%MOD;
}
g[0]=1;
g[1]=f[1];
for(int i=2;i<=MAXN-5;i++)
{
g[i]=((long long)g[i-2]*f[i])%MOD;
}
scanf("%d",&T);
while(T--)
{
scanf("%d %d",&n,&m);
int Res=((long long)g[min(n,m)*2-1]*g[min(n,m)*2-1])%MOD;
//printf("%d??\n",Res);
Res=((long long)Res*Pow(f[2*min(n,m)],max(n,m)-min(n,m),MOD))%MOD;
printf("%d\n",Res);
}
}
D
zdj是怎么10min做完的/bx
一眼看没思路,dj给我讲懂得
首先为了保证最大,我们发现区间得\(L\)一定是\(x_i+1\)得形式,\(R\)一定是\(x_i-1\)得形式
然后我们考虑\(x_i,x_{i+1}\),可以发现两者\(y_{i+1}-y_i\)得差就是\(L_i-R_{i}\),\(L_i\)表示\(L=x_i+1\)的区间,\(R_i\)表示\(R=x_{i+1}-1\)的区间
然后我们就可以直接得到差值,为了最优,不难发现\(x_i,x_{i+1}\)这一段不能同时有
这样我们就可以得到\(L,R\)的分布情况,为了最后答案最优我们排序之后匹配端点即可,因为如果不是可以交换得到更优
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=2e5+5;
int n;
int x[MAXN];
int y[MAXN];
int c[MAXN];
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&x[i]);
}
for(int i=1;i<=n;i++)
{
scanf("%d",&y[i]);
}
x[0]=-2e9;
x[n+1]=2e9+1;
vector<pair<int,int> >L,R;
for(int i=0;i<=n;i++)
{
c[i]=y[i+1]-y[i];
if(c[i]>0)
{
L.push_back(make_pair(x[i]+1,c[i]));
}
else
{
R.push_back(make_pair(x[i+1]-1,-c[i]));
}
}
// for(int i=0;i<L.size();i++)
// {
// printf("%d %d\n",L[i].first,L[i].second);
// }
// for(int i=0;i<R.size();i++)
// {
// printf("%d %d\n",R[i].first,R[i].second);
// }
int Res=1e9;
int Pi=0;
for(int i=0;i<L.size();i++)
{
while(L[i].second)
{
Res=min((long long)Res,(long long)R[Pi].first-L[i].first);
if(R[Pi].second<=L[i].second)
{
L[i].second-=R[Pi].second;
++Pi;
}
else
{
R[Pi].second-=L[i].second;
L[i].second=0;
}
}
}
if(Res>=1e9)
{
printf("-1");
}
else
{
printf("%d\n",Res);
}
}
E
脱欧不补。。
ARC147
A
模拟即可,时间复杂度类似于拓欧
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=5e5+5;
int n;
int a[MAXN];
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&n);
multiset<int>S;
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
S.insert(a[i]);
}
int Res=0;
while(S.size()>1)
{
auto it=S.begin();
auto jt=S.end();
--jt;
int Nw=((*jt)%(*it));
S.erase(jt);
if(Nw)
{
S.insert(Nw);
}
++Res;
}
printf("%d\n",Res);
}
B
恶心细节题
直接对奇偶不对的点配对即可,要注意随时维护序列
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=405;
int n;
int P[MAXN];
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&P[i]);
}
vector<int>Odd;
vector<int>Even;
for(int i=1;i<=n;i++)
{
if((i&1)!=(P[i]&1))
{
if((i&1))
{
Odd.push_back(i);
}
else
{
Even.push_back(i);
}
}
}
vector<pair<int,int> >Ans;
while(1)
{
int Pi=-1;
int Pj=-1;
for(int i=1;i<=n;i++)
{
if((i&1)!=(P[i]&1))
{
if((i&1))
{
Pi=i;
}
else
{
Pj=i;
}
}
}
if(Pi==-1)
{
break;
}
int To=Pj-1;
while(Pi>To)
{
swap(P[Pi],P[Pi-2]);
Ans.push_back(make_pair(1,Pi-2));
Pi-=2;
}
while(Pi<To)
{
swap(P[Pi],P[Pi+2]);
Ans.push_back(make_pair(1,Pi));
Pi+=2;
}
swap(P[Pi],P[Pj]);
Ans.push_back(make_pair(0,Pi));
}
for(int i=1;i<=n;i+=2)
{
for(int j=1;j+2<=n;j+=2)
{
if(P[j]>P[j+2])
{
swap(P[j],P[j+2]);
Ans.push_back(make_pair(1,j));
}
}
}
for(int i=1;i<=n;i+=2)
{
for(int j=2;j+2<=n;j+=2)
{
if(P[j]>P[j+2])
{
swap(P[j],P[j+2]);
Ans.push_back(make_pair(1,j));
}
}
}
int Tot=0;
printf("%d\n",Ans.size());
for(int i=0;i<Ans.size();i++)
{
if(Ans[i].first==0)
{
printf("A %d\n",Ans[i].second);
Tot++;
}
else
{
printf("B %d\n",Ans[i].second);
}
}
}
C
想不到的贪心/kk
考虑最大的\(L\)和最小的\(R\),如果\(L\le R\)答案为\(0\)
否则可以证明把所有\(x_i\)全放在\([L,R]\)之内一定不劣
证明的话就考虑如果有一个不满足,我们一定可以调整它到\([L,R]\)之内一定不劣,因为\(L,R\)一定动不了
这样我们就可以确定\(L,R\)所在区间一定要固定在\(L,R\),再递归解决即可
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=3e5+5;
int n;
int L[MAXN];
int R[MAXN];
int cmp(int x,int y)
{
return x>y;
}
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d %d",&L[i],&R[i]);
}
sort(L+1,L+1+n,cmp);
sort(R+1,R+1+n);
long long Res=0;
for(int i=1;i<=n;i++)
{
Res+=(long long)max(0,L[i]-R[i])*(n-2*i+1);
}
printf("%lld\n",Res);
}
D
想不到的结论/kk
把\(S\)看成\(01\)串,\(S_{i}\rightarrow S_{i+1}\)即是\(\oplus 2^{x_i}\)
现确定\(S_0\),我们发现如果确定了\(x\)序列,我们可以得到\(a_i,b_i\)表示\(i\)这个元素最开始在/不在\(S_0\)时出现的次数,其中\(b_i=n-a_i\)
直接写式子
\(\sum\limits_{S_0}(\prod\limits_{i\in S_0}a_i\prod\limits_{i\notin S_0}n-a_i)\),如果固定除\(i\)位以外的位,则第\(i\)位的贡献为\(n\)
则上面那个式子和\(x\)无关,为\(n^m\)
最后的答案即为\(n^mm^{n-1}\)
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MOD=998244353;
int Pow(int a,int b,int p)
{
int res=1;
int base=a;
while(b)
{
if(b&1)
{
res=((long long)res*base)%p;
}
base=((long long)base*base)%p;
b>>=1;
}
return res;
}
int n,m;
int main()
{
scanf("%d %d",&n,&m);
printf("%d\n",((long long)Pow(n,m,MOD)*Pow(m,n-1,MOD))%MOD);
}
E
比C,D简单多了/kk
问题转换成最少要多少个二元组插入给定序列使得排序后满足\(A_i\ge B_i\)
最开始序列\(A_n<B_n\),我们考虑找\(\ge B_n\)的\(A_i\)且\(B_i\)最小,线段树维护一下即可
Show Code
// LUOGU_RID: 128896897
#include<bits/stdc++.h>
#define ls Tree[p].lc
#define rs Tree[p].rc//
using namespace std;
const int MAXN=3e5+5;
int n;////
struct node{
int a,b;
}v[MAXN];
priority_queue<int>A,B;
struct Seg{
pair<int,int> date;
int lc,rc;
}Tree[MAXN*20];
multiset<int>S[MAXN*20];
int rt;
int cnt_node;
void push_up(int p)
{
Tree[p].date.first=1e9+1;
if(ls)
{
Tree[p].date=min(Tree[p].date,Tree[ls].date);
}
if(rs)
{
Tree[p].date=min(Tree[p].date,Tree[rs].date);
}
}
void Insert(int &p,int l,int r,int k,int x)
{
if(!p)
{
++cnt_node;
p=cnt_node;
Tree[p].lc=0;
Tree[p].rc=0;
Tree[p].date.first=1e9+1;
}
if(l==r)
{
S[p].insert(x);
Tree[p].date.first=(*(S[p].begin()));
Tree[p].date.second=l;
return;
}
int mid=(l+r)>>1;
if(k<=mid)
{
Insert(ls,l,mid,k,x);
}
else
{
Insert(rs,mid+1,r,k,x);
}
push_up(p);
}
void Delete(int &p,int l,int r,int k,int x)
{
if(!p)
{
++cnt_node;
p=cnt_node;
Tree[p].lc=0;
Tree[p].rc=0;
Tree[p].date.first=1e9+1;
}
if(l==r)
{
S[p].erase(S[p].find(x));
if(S[p].size())
{
Tree[p].date.first=(*(S[p].begin()));
Tree[p].date.second=l;
}
else
{
Tree[p].date.first=1e9+1;
}
return;
}
int mid=(l+r)>>1;
if(k<=mid)
{
Delete(ls,l,mid,k,x);
}
else
{
Delete(rs,mid+1,r,k,x);
}
push_up(p);
}
pair<int,int>Query(int p,int l,int r,int ql,int qr)
{
if(!p)
{
return make_pair(1e9+1,0);
}
if(l>=ql&&r<=qr)
{
return Tree[p].date;
}
int mid=(l+r)>>1;
pair<int,int>Res=make_pair(1e9+1,0);
if(ql<=mid)
{
Res=min(Res,Query(ls,l,mid,ql,qr));
}
if(qr>mid)
{
Res=min(Res,Query(rs,mid+1,r,ql,qr));
}
return Res;
}
int main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&n);
int Res=0;
for(int i=1;i<=n;i++)
{
scanf("%d %d",&v[i].a,&v[i].b);
if(v[i].a<v[i].b)
{
A.push(v[i].a);
B.push(v[i].b);
Res++;
}
else
{
Insert(rt,1,1e9,v[i].a,v[i].b);
}
}
while(A.size())
{
while(A.size()&&(A.top()>=B.top()))
{
A.pop();
B.pop();
}
if(B.size())
{
int neb=(B.top());
B.pop();
pair<int,int>Vot=Query(rt,1,1e9,neb,1e9);
if(Vot.first>neb)
{
printf("-1");
return 0;
}
Delete(rt,1,1e9,Vot.second,Vot.first);
++Res;
B.push(Vot.first);
}
}
printf("%d\n",n-Res);
}
ARC167
A
简单贪心
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MAXN=2e5+5;
int n,m;
int A[MAXN];
long long Res=0;
int cmp(int x,int y)
{
return x>y;
}
int B[MAXN];
signed main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d %d",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%d",&A[i]);
}
sort(A+1,A+1+n,cmp);
for(int i=1;i<=m;i++)
{
B[i]=A[i];
}
reverse(B+1,B+1+m);
for(int i=m+1;i<=n;i++)
{
B[i-m]+=A[i];
}
for(int i=1;i<=m;i++)
{
Res+=((long long)B[i]*B[i]);
}
printf("%lld\n",Res);
}
B
拆质因数后直接列柿子
最后要除二向下取整
Show Code
#include<bits/stdc++.h>
#define int __int128
using namespace std;
void read(__int128 &x) {
x = 0;
int f = 1;
char s = getchar();
while (s > '9' || s < '0') {
if (s == '-')
f = -1;
s = getchar();
}
while (s >= '0' && s <= '9') {
x = (x << 3) + (x << 1) + (s - '0');
s = getchar();
}
x *= f;
}
void write(__int128 x) {
if (x < 0) {
putchar('-');
x = (~x) + 1;
}
if (x > 9) {
write(x / 10);
}
putchar(x % 10 + '0');
}
const int MOD=998244353;
int A,B;
signed main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
read(A);
read(B);
int NT=B;
B%=MOD;
int Now=A;
int Mul=1;
bool f=0;
if(NT%2==0)
{
f=1;
}
for(int i=2;i<=Now/i;i++)
{
if(Now%i==0)
{
int ae=0;
while(Now%i==0)
{
ae++;
Now/=i;
}
if((ae*NT)%2)
{
f=1;
}
ae=(ae*B)%MOD;
ae=(ae+1)%MOD;
Mul=(Mul*ae)%MOD;
}
}
if(Now>1)
{
int ae=1;
if((ae*NT)%2)
{
f=1;
}
ae=(ae*B)%MOD;
ae=(ae+1)%MOD;
Mul=(Mul*ae)%MOD;
}
if(f)
{
//printf("fuck\n");
int inv2=(MOD-MOD/2);
Mul=(Mul*B)%MOD;
Mul=(Mul*inv2)%MOD;
Mul%=MOD;
write(Mul);
}
else
{
int inv2=(MOD-MOD/2);
Mul=(Mul*B)%MOD;
Mul=(Mul-1+MOD)%MOD;
Mul=(Mul*inv2)%MOD;
Mul%=MOD;
write(Mul);
}
}
C
反正我是想不到
考虑差分,计算出\(g_i\)表示只用\(\le i\)的边最多能连多少条边
考虑什么时候能连边,我们把权值\(\le i\)的点拉出来,位置序列记为\(g\)
对于\(g\),我们考虑统计\(j,j+1\)是否能产生贡献,也即\(g_{j+1}-g_{j}\le K\)
考虑枚举\(k\le K\),则当\(g_{j+1}-g_j=K\)时产生贡献,方案数位\(\binom{n-k}{i-1}\)
最后全部求和即可
Show Code
#include<bits/stdc++.h>
using namespace std;
const int MOD=998244353;
const int MAXN=5005;
int n;
int K;
int a[MAXN];
int C[MAXN][MAXN];
int g[MAXN];
int fac[MAXN];
signed main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d %d",&n,&K);
C[0][0]=1;
fac[0]=1;
for(int i=1;i<=n;i++)
{
C[i][0]=1;
fac[i]=((long long)fac[i-1]*i)%MOD;
for(int j=1;j<=i;j++)
{
C[i][j]=((long long)C[i-1][j]+C[i-1][j-1])%MOD;
}
}
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
}
sort(a+1,a+1+n);
int Res=0;
g[0]=1;
for(int i=2;i<=n;i++)
{
g[i]=0;
for(int k=1;k<=K;k++)
{
int gp=fac[i];
gp=((long long)gp*fac[n-i])%MOD;
gp=((long long)gp*C[n-k][i-1])%MOD;
gp=((long long)gp*(i-1))%MOD;
g[i]=((long long)g[i]+gp)%MOD;
}
}
for(int i=2;i<=n;i++)
{
int Tt=((long long)g[i]-g[i-1]+MOD)%MOD;
Tt=((long long)Tt*a[i])%MOD;
Res=((long long)Res+Tt)%MOD;
}
printf("%d\n",Res);
}
D
不难发现贪心策略是从低到高考虑,每次看当前是否存在不在当前环最小的元素\(\le i\)
模拟一下,你会发现每次操作的都是\(1\)所在的环
所以只用维护值域指针即可
Show Code
// LUOGU_RID: 130071927
#include<bits/stdc++.h>
using namespace std;
const int MAXN=2e5+5;//
int T;
int n;
int P[MAXN];///
int fa[MAXN];///
int R[MAXN];
int Vis[MAXN];
int Cnt=0;
void dfs(int x)
{
if(Vis[x])
{
return;
}
Vis[x]=1;
++Cnt;
dfs(P[x]);
}
signed main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&T);
while(T--)
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
Vis[i]=0;
scanf("%d",&P[i]);
R[P[i]]=i;
}
Cnt=0;
dfs(1);
int Pi=1;
for(int i=1;i<=n;i++)
{
while(Vis[Pi]&&(Pi<=n))
{
++Pi;
}
if(Pi==n+1)
{
break;
}
if(P[i]>Pi||(Cnt==i))
{
int Pos=R[Pi];
dfs(Pos);
swap(P[i],P[Pos]);
R[P[i]]=i;
R[P[Pos]]=Pos;
++Pi;
}
}
for(int i=1;i<=n;i++)
{
printf("%d ",P[i]);
}
printf("\n");
}
}
E
牛仔哒题
Show Code
#include<bits/stdc++.h>
using namespace std;
int T;
int n;
signed main()
{
// freopen("date.in","r",stdin);
// freopen("date.out","w",stdout);
scanf("%d",&T);
while(T--)
{
scanf("%d",&n);
if(n%2==0)
{
if(n==2)
{
printf("No\n");
}
else
{
printf("Yes\n");
printf("0 0 2 0 %d %d\n",n/2,n/2);
}
}
else
{
if(n<9)
{
printf("No\n");
}
else
{
printf("Yes\n");
printf("0 0 3 1 %d %d\n",(n-3)/2,(n-1)/2);
}
}
}
}

 封闭心底 朝远处大海展翅飞去
封闭心底 朝远处大海展翅飞去

 浙公网安备 33010602011771号
浙公网安备 33010602011771号