分治，倍增

《分治，倍增》

其实全是二分

CF1059E Split the Tree

考虑贪心

为了使链的数量小，肯定是使每条链的长度更长

从叶子开始拓展，对于当前节点，选的儿子一定是能向上拓展最长的

用类似\(LCA\)的倍增

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN=1e5+5;
int n,L,S;
int a[MAXN];
int x;
int Fa[MAXN];
vector<int>g[MAXN];
int Res=0;
pair<int,int>Up[MAXN];
int dep[MAXN];
int Sum[MAXN];
int dp[MAXN][25]; 
void dfs(int x)
{
	vector<int>Suit;
	if(!g[x].size())
	{
		Up[x].first=1;
		Up[x].second=a[x];
		if(a[x]>S)
		{
			//printf("?");
			printf("-1");
			exit(0);
		}
		if(x==1)
		{
			Res++;
		}
		return;
	}
	for(int i=0;i<g[x].size();i++)
	{
		int v=g[x][i];
		dep[v]=dep[x]+1;
		Sum[v]=Sum[x]+a[v];
		dp[v][0]=x;
		for(int j=1;j<=20;j++){
			dp[v][j]=dp[dp[v][j-1]][j-1];
		}
		dfs(v);
	
		pair<int,int>sgs=Up[v];
		if(sgs.first+1<=L&&sgs.second+a[x]<=S)
		{
			Suit.push_back(v);
		}
		else
		{
			Res++;
		}
	
	}
	if(!Suit.size())
	{
		Up[x].first=1;
		Up[x].second=a[x];
		if(x==1)
		{
			Res++;		
		}
		if(a[x]>S)
		{
			//printf("?");
			printf("-1");
			exit(0);
		}
		return;
	}
	int Mini=0x3f3f3f3f;
	int idi=0;
	for(int i=0;i<Suit.size();i++)
	{
		int ORG=Suit[i];
		int Now=Suit[i];
		pair<int,int>Nod=Up[Now];
		for(int j=20;j>=0;j--)
		{
			int FF=dp[Now][j];
			if((dep[ORG]-dep[FF])+Nod.first<=L&&((Sum[ORG]-Sum[FF])+Nod.second<=S))
			{
				Now=FF;
			}
		}
		int Wei=(dep[Now]);
		if(Wei<Mini)
		{
			idi=ORG;
			Mini=Wei;
		 } 
	}
	for(int i=0;i<Suit.size();i++)
	{
		int ORG=Suit[i];
		if(ORG==idi)
		{
			pair<int,int>New;
			New.first=Up[idi].first+1;
			New.second=Up[idi].second+a[x];
			Up[x]=New;
			if(x==1)
			{
				Res++;
				
			}
		}
		else
		{
			Res++;
		}
	}
}
signed main()
{
	scanf("%lld %lld %lld",&n,&L,&S);
	for(int i=1;i<=n;i++)
	{
		scanf("%lld",&a[i]);
	} 
	for(int i=2;i<=n;i++)
	{
		scanf("%lld",&x);
		Fa[i]=x;
		g[x].push_back(i);
	}
	dfs(1);
	printf("%lld\n",Res);
}
//3 3 2200000000
//1000000000 1000000000 1000000000
//1 2

CF1394C Boboniu and String

相似就是\(B,N\)的数量相同

那么对于每一个操作，实际上要么是\(|B|,|N|\)单独\(\pm1\),或是共同\(\pm1\)

如果把他放在平面直角坐标系

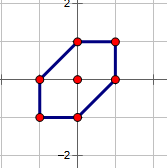
上面的边界即为可达

二分答案\(Mid\)

然后构造一个\(T\)

实际上首先\(T与S_i\)的横纵坐标差的最大值要小于\(Mid\)

从图上开，这样是一个正方形的边框，但实际上是六边形

所以还要加上一个两次函数的限制

\[x-Mid\leq x'\leq x+Mid \\ y-Mid\leq y'\leq y+Mid \\ (x-y)-Mid\leq (x'-y')\leq (x-y)+Mid \]

解出\(x,y,(x-y)\),然后解不等式即可

#include<bits/stdc++.h>
using namespace std;
const int MAXN=3e5+5;
int n;
string s;

int detA[MAXN],detB[MAXN];
int AL,AR,BL,BR,detL,detR,A,B;
bool check(int Mid)
{
	AL=0,AR=1e6,BL=0,BR=1e6;
	detL=-1e6;
	detR=1e6;
	for(int i=1;i<=n;i++)
	{
		AL=max(AL,detA[i]-Mid);
		AR=min(AR,detA[i]+Mid);
		BL=max(BL,detB[i]-Mid);
		BR=min(BR,detB[i]+Mid);
		detL=max(detL,detA[i]-detB[i]-Mid);
		detR=min(detR,detA[i]-detB[i]+Mid);
	}
	if(AL>AR||BL>BR||detL>detR)
	{
	//	printf("%d %d\n",detL,detR);
		return 0;
	}
	int NXL=BL+detL;
	int NXR=BR+detR;
//	printf("?");
	if(NXR<AL||NXL>AR)
	{
		return 0;
	}
	NXL=max(NXL,AL);
	NXR=min(NXR,AR);
	A=NXL;
	int NYL=A-detR;
	int NYR=A-detL;
	NYL=max(NYL,BL);
	NYR=min(NYR,BR);
	B=NYL;
	return 1;
}
//(x,y) max(abs(x-X),abs(y-Y))<=d
//(x-y) 
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	{
		cin>>s;
		for(int j=0;j<s.size();j++)
		{
			if(s[j]=='B')
			{
				detA[i]++;
			}
			else
			{
				detB[i]++;
			}
		}
	//	printf("%d %d\n",detA[i],detB[i]);
	}
	int l=0;
	int r=1e6;
	int key;
	while(l<=r)
	{
		int mid=(l+r)>>1;
		if(check(mid))
		{
			key=mid;
			r=mid-1;
		}
		else
		{
			l=mid+1; 
		}
	 }
	printf("%d\n",key);
	check(key);
	//printf("%d\n",check(12));
	//printf("%d %d %d %d\n",AL,AR,BL,BR);
	for(int i=1;i<=A;i++)
	{
		printf("B");
	}
	for(int i=1;i<=B;i++)
	{
		printf("N");
	}
 } 

CF627D Preorder Test

首先可以二分答案\(Mid\)

当前限制为\(Mid\),权值大于\(Mid\)为能走的节点

我们设\(dp_i\)为以\(i\)为根时能走最多可行点

\[dp_x=1+(dp_v)[dp_v=Siz_v]+Max(dp(v)[dp_v\neq Siz_v]) \]

由于根不是指定的

所以要换根，有点复杂，但思路简单

#include<bits/stdc++.h>
using namespace std;
const int MAXN=2e5+5;
int n,k;
int a[MAXN];
int x,y;
vector<int>g[MAXN];
int dp1[MAXN];
int dp2[MAXN];
int dp_up[MAXN];
int Siz[MAXN];
int Aiv[MAXN];
void dfs1(int x,int f)
{
	Siz[x]=1;
	for(int i=0;i<g[x].size();i++)
	{
		int v=g[x][i];
		if(v==f)
		{
			continue;
		}
		dfs1(v,x);
		Siz[x]=Siz[x]+Siz[v];
	}
	if(!Aiv[x])
	{
		dp1[x]=0;
		return;
	}
	dp1[x]=1;
	int Maxi=0;
	for(int i=0;i<g[x].size();i++)
	{
		int v=g[x][i];
		if(v==f)
		{
			continue;
		}
		if(dp1[v]==Siz[v])
		{
			dp1[x]+=dp1[v];
		}
		else
		{
			Maxi=max(Maxi,dp1[v]);
		}
	}
	dp1[x]+=Maxi;
}
void dfs2(int x,int f)
{
	int Sum=0;
	int Fir=0;
	int Sec=0;
	if(Aiv[x])
	{
		Sum=1;
		for(int i=0;i<g[x].size();i++)
		{
			int v=g[x][i];
			if(v==f)
			{
				continue;
			}
			if(dp1[v]==Siz[v])
			{
				Sum+=dp1[v];
			}
			else
			{
				if(dp1[v]>=Fir)
				{
					Sec=Fir;
					Fir=dp1[v];
				}
				else if(dp1[v]>Sec)
				{
					Sec=dp1[v];
				}
			}
		 
		}
	
		if(dp_up[x]==n-Siz[x])
		{
			Sum+=dp_up[x];
		}
		else
		{
			if(dp_up[x]>=Fir)
			{
				Sec=Fir;
				Fir=dp_up[x];
			}
			else if(dp_up[x]>Sec)
			{
				Sec=dp_up[x];
			}
		}
		dp2[x]=Sum+Fir;
	}
	else
	{
		dp2[x]=0;
	}
	
	for(int i=0;i<g[x].size();i++)
	{
		int v=g[x][i];
		if(v==f)
		{
			continue;
		}
		if(Aiv[x])
		{
			if(dp1[v]==Siz[v])
			{
				dp_up[v]=dp2[x]-dp1[v];
			 }
			 else
			 {
			 	if(dp1[v]==Fir)
			 	{
			 		dp_up[v]=dp2[x]-Fir+Sec;
				 }
				 else
				 {
				 	dp_up[v]=dp2[x];
				 }
			 }
		}
		else
		{
			dp_up[v]=0;	
		}
		
		dfs2(v,x);
	}
 } 
bool check(int mid)
{
	for(int i=1;i<=n;i++)
	{
		if(a[i]>=mid)
		{
			Aiv[i]=1;
		 } 
		 else
		 {
		 	Aiv[i]=0;
		 }
	}
	dfs1(1,0);
	dp2[1]=dp1[1];
	dfs2(1,0);
	int ssMaxi=0;
	for(int i=1;i<=n;i++)
	{
		ssMaxi=max(ssMaxi,dp2[i]);
	}
	return ssMaxi>=k;
}
signed main()
{
	scanf("%d %d",&n,&k);
	for(int i=1;i<=n;i++)
	{
		scanf("%d",&a[i]);
	}
	for(int i=1;i<n;i++)
	{
		scanf("%d %d",&x,&y);
		g[x].push_back(y);
		g[y].push_back(x);
	}
	int l=1;
	int r=1000000;
	int key;
	while(l<=r)
	{
		int mid=(l+r)>>1;
		if(check(mid))
		{
			key=mid;
			l=mid+1;
		}
		else
		{
			r=mid-1;
		}
	} 
	printf("%d\n",key);
}