uva 1416 Warfare And Logistics

题意：

给出一个无向图，定义这个无向图的花费是

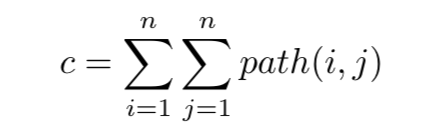
其中path(i,j)，是i到j的最短路。

去掉其中一条边之后，花费为c’，问c’ – c的最大值，输出c和c’。

思路：

枚举每条边，每次把这条边去掉，然后以每个点为起点，跑一次Dijkstra，再计算总花费。

这样的复杂度为O(mn^2log(n))，这个复杂度刚好卡着时间过，所以是暴力，更优的方法是最短路树（待学习。

代码：

#include <stdio.h>
#include <string.h>
#include <vector>
#include <queue>
using namespace std;

struct edge
{
    int to,cost;
    int id;
    
    edge(int uu,int vv,int idd)
    {
        to = uu;
        cost = vv;
        id = idd;
    }
};

const int maxn = 105;

typedef pair<long long,int> pii;
long long d[maxn];
vector<edge> g[maxn];
bool ma[1005];

void adde(int st,int en,int cost,int id)
{
    g[st].push_back(edge(en,cost,id));
}

void dij(int s,int n)
{
    for (int i = 0;i <= n;i++) d[i] = 1e16;
    
    priority_queue<pii,vector<pii>,greater<pii> > pq;
    
    pq.push(pii(0,s));
    
    d[s] = 0;
    
    //printf("***\n");
    
    while (!pq.empty())
    {
        pii x = pq.top();pq.pop();
        
        int v = x.second;
        
        if (d[v] < x.first) continue;
        
        for (int i = 0;i < g[v].size();i++)
        {
            edge e = g[v][i];
            
            if (d[e.to] > d[v] + e.cost)
            {
                d[e.to] = d[v] + e.cost;
                pq.push(pii(d[e.to],e.to));
            }
        }
    }
    
    //printf("***\n");
}

void dijk(int s,int n)
{
    for (int i = 0;i <= n;i++) d[i] = 1e16;
    
    priority_queue<pii,vector<pii>,greater<pii> > pq;
    
    pq.push(pii(0,s));
    
    d[s] = 0;
    
    while (!pq.empty())
    {
        pii x = pq.top();pq.pop();
        
        int v = x.second;
        
        if (d[v] < x.first) continue;
        
        for (int i = 0;i < g[v].size();i++)
        {
            edge e = g[v][i];
            
            if (ma[e.id]) continue;
            
            if (d[e.to] > d[v] + e.cost)
            {
                d[e.to] = d[v] + e.cost;
                pq.push(pii(d[e.to],e.to));
            }
        }
    }
    
    //printf("***\n");
}

int main()
{
    int n,m,l;
    
    while (scanf("%d%d%d",&n,&m,&l) != EOF)
    {
        for (int i = 0;i <= n;i++) g[i].clear();
        
        for (int i = 0;i < m;i++)
        {
            int a,b,c;
            
            scanf("%d%d%d",&a,&b,&c);
            
            adde(a,b,c,i);
            adde(b,a,c,i);
        }
        
        long long ans = 0;
        
        for (int i = 1;i <= n;i++)
        {
            
            
            dij(i,n);
            
            for (int j = 1;j <= n;j++)
            {
                if (d[j] == 1e16) d[j] = l;
                ans += d[j];
            }
        }
        
        
        
        long long res = 0;
        long long tmp = 0;
        
        for (int i = 0;i < m;i++)
        {
            ma[i] = 1;
            
            long long orz = 0;
            
            for (int j = 1;j <= n;j++)
            {
                dijk(j,n);
                
                for (int k = 1;k <= n;k++)
                {
                    if (d[k] == 1e16) d[k] = l;
                    orz += d[k];
                }
            }
            
            if (orz - ans > tmp)
            {
                res = orz;
                tmp = orz - ans;
            }
            
            ma[i] = 0;
        }
        
        printf("%lld %lld\n",ans,res);
    }
    
    return 0;
}