R-正态性检验实例

数据

price.csv文件（一列价格差值的数据，包含标题）

问题描述

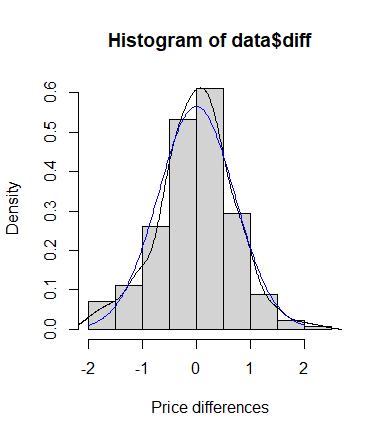
• 利用price.csv数据绘制数据直方图，并添加概率密度曲线(density)和估计概率密度曲线(dnorm) 。
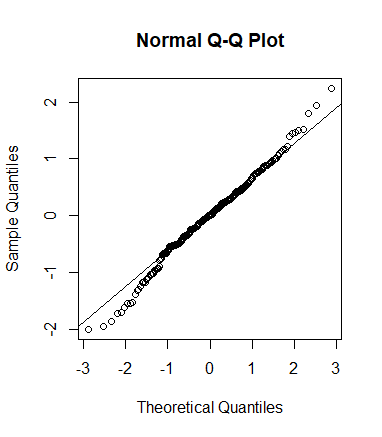
• 绘制出qqplot及其拟合线。
• 用Shapiro和Kolmogorov-Smirnov检验判断该数据是否符合正态分布。

代码实现

?

1 2 3 4 5 6 7 8 9 10 11 12

data = read.csv("price.csv", header = T) hist(data$diff, freq = F, xlab = 'Price differences', ylab = 'Density')  #绘制直方图 lines(density(data$diff), col = 'black')  #添加概率密度曲线 x = seq(-2, 2, len = 252) lines(x, dnorm(x, mean(data$diff), sd(data$diff)), col= 'blue')  #添加估计概率密度曲线   qqnorm(data$diff)  #绘制qqplot qqline(data$diff)  #绘制拟合线   shapiro.test(data$diff)   ks.test(data$diff, 'pnorm', mean = mean(data$diff), sd = sd(data$diff))

结果展示

?

1 2 3 4 5 6 7 8 9 10 11 12 13 14

> shapiro.test(data$diff)       Shapiro-Wilk normality test   data:  data$diff W = 0.99146, p-value = 0.1503   > ks.test(data$diff, 'pnorm', mean = mean(data$diff), sd = sd(data$diff))       One-sample Kolmogorov-Smirnov test   data:  data$diff D = 0.052668, p-value = 0.4867 alternative hypothesis: two-sided

　　两种检验均表明该数据服从正态分布。