转载:【AI系统】EfficientFormer 系列
本文主要介绍一种轻量化的 Transformer 结构,在获得高性能的同时,能够保持一定的推理速度。以延迟为目标进行优化设计。通过延迟分析重新探讨 ViT 及其变体的设计原则。
EfficientFormer V1 模型
EfficientFormer V1:基于 ViT 的模型中使用的网络架构和具体的算子,找到端侧低效的原因。然后引入了维度一致的 Transformer Block 作为设计范式。最后,通过网络模型搜索获得不同系列的模型 —— EfficientFormer。
大多数现有方法通过从服务器 GPU 获得的计算复杂性(MAC)或吞吐量(图像/秒)来优化 Transformer 的推理速度。但是这些指标不能反映实际的设备延迟。为了清楚地了解哪些操作和设计选择会减慢边缘设备上 VIT 的推断,在下图中作者作者对不同模型在端侧运行进行了一些分析,主要是分为 ViT 对图像进行分块的 Patch Embedding、Transformer 中的 Attention 和 MLP,另外还有 LeViT 提出的 Reshape 和一些激活等。提出了下面几个猜想。
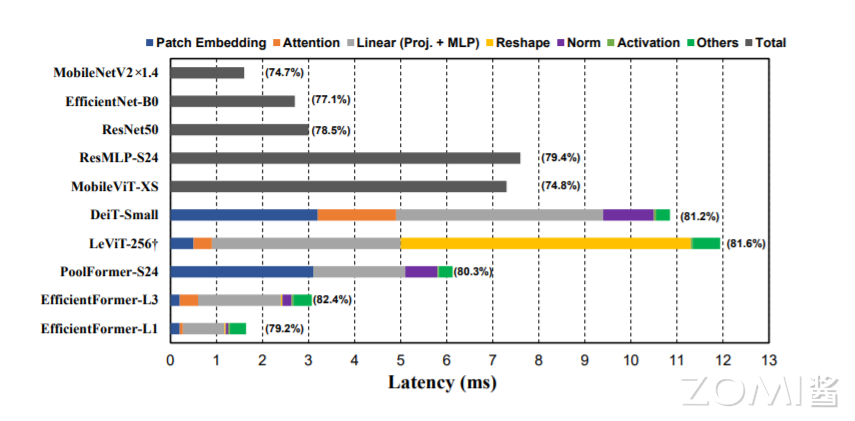
观察 1:在移动设备上,具有大核和步长的 patch 嵌入是一个速度瓶颈。
patch 嵌入通常使用一个不重叠的卷积层来实现,该层具有较大的内核大小和步长。一种普遍的看法是,Transformer 网络中 patch 嵌入层的计算成本不显著或可以忽略不计。然而,在上图中比较了具有大核和大步长的 patch 嵌入模型,即 DeiT-S 和 PoolFormer-s24,以及没有它的模型,即 LeViT-256 和 EfficientFormer,结果表明,patch 嵌入反而是移动设备上的速度瓶颈。
大多数编译器都不支持大型内核卷积,并且无法通过 Winograd 等现有算法来加速。或者,非重叠 patch 嵌入可以由一个具有快速下采样的卷积 stem 代替,该卷积 stem 由几个硬件效率高的 3×3 卷积组成。
#stem 以一些普通卷积组成
def stem(in_chs, out_chs):
return nn.Sequential(
nn.Conv2d(in_chs, out_chs // 2, kernel_size=3, stride=2, padding=1),
nn.BatchNorm2d(out_chs // 2),
nn.ReLU(),
nn.Conv2d(out_chs // 2, out_chs, kernel_size=3, stride=2, padding=1),
nn.BatchNorm2d(out_chs),
nn.ReLU(), )
观察 2:一致的特征维度对于选择 token 混合器很重要。MHSA 不一定是速度瓶颈。
最近的工作将基于 ViT 的模型扩展到 MetaFormer,该架构由 MLP 块和未指定的 token 混合器组成。在构建基于 ViT 的模型时,选择 token 混合器是一个重要的设计选择。token 混合器的选择有很多:传统的 MHSA 混合器,它们具有全局感受野;更复杂的移位窗口注意;或者像池化这样的非参数化操作符。
作者将比较范围缩小到两种 token 混合器,池化和 MHSA,其中选择前者是为了简单和高效,而后者是为了更好的性能。大多数公开的移动编译器目前不支持更复杂的 token 混合器,如移位窗口,因此作者将其排除在范围之外。此外,由于本文专注于在没有轻量级卷积帮助的情况下构建体系结构,因此没有使用深度卷积来取代池化。
为了解两个 token 混合器的延迟,作者执行以下两个比较:
首先,通过比较 PoolFormer-s24 和 LeViT-256,作者发现 reshape 操作是 LeViT-256 的一个瓶颈。LeViT-256 的大部分是用 CONV on 4D tensor 实现的,在特征转发到 MHSA 时需要频繁的 reshape 操作,因为 MHSA 必须在 3D tensor 上进行注意(丢弃注意力头的额外尺寸)。reshape 的广泛使用限制了 LeViT 在移动设备上的速度。另一方面,当网络主要由基于 CONV 的实现组成时,池化自然适合 4D 张量,例如,CONV 1×1 作为 MLP 实现,CONV stem 用于下采样。因此,PoolFormer 具有更快的推理速度。
其次,通过比较 DeiT-S 和 LeViT-256,作者发现,如果特征尺寸一致且不需要 reshape,MHSA 不会给手机带来显著的开销。虽然计算量更大,但具有一致 3D 特征的 DeiT-S 可以达到与新 ViT 变体(即 LeViT-256)相当的速度。
观察 3:CONV-BN 比 LN-Linear 更适合延迟,准确性缺陷通常是可以接受的。
选择 MLP 实现是另一个重要的设计选择。通常,会选择两个选项之一:带 3D 线性投影(proj)的 LayerNorm(LN)和带 BatchNorm(BN)的 CONV1×1。CONV-BN 更适合低延迟,因为 BN 可以折叠到之前的卷积用于推理加速,而 LN 仍在推理阶段收集运行统计信息,从而导致延迟。根据本文的实验结果和之前的工作,LN 引入的延迟约占整个网络延迟的 10%-20%。
观察 4:非线性延迟取决于硬件和编译器。
最后,作者研究了非线性,包括 GeLU、ReLU 和 HardSwish。之前的工作表明 GeLU 在硬件上效率不高,会减慢推理速度。然而,作者观察到,GeLU 受到 iPhone 12 的良好支持,几乎不比它的对手 ReLU 慢。
相反,在本文的实验中,HardSwish 的速度惊人地慢,编译器可能无法很好地支持它(LeViT-256 使用 HardSwish 的延迟为 44.5 ms,而使用 GeLU 的延迟为 11.9 ms)。作者的结论是,考虑到手头的特定硬件和编译器,非线性应该根据具体情况来确定。
EfficientFormer 结构
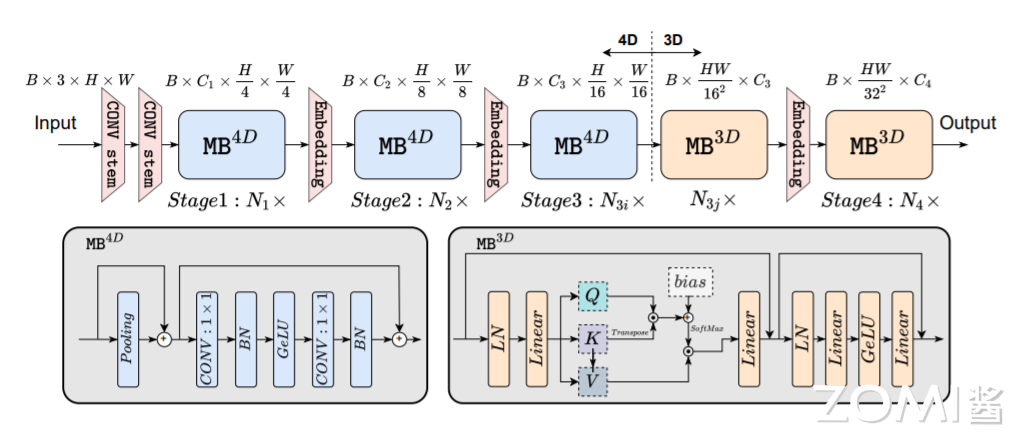
基于延迟分析,作者提出了 EfficientFormer 的设计,如上图所示。该网络由 patch 嵌入(PatchEmbed)和 meta transformer 块堆栈组成,表示为 MB:
$$
y = \prod_{i}{m}MB_{i}(PatchEmbed(X_{0}))
$$
其中 $X_{0}$ 是 Batch 大小为 B、空间大小为 $[H,W]$ 的输入图像,$y$ 是所需输出,$m$ 是块的总数(深度)。$MB$ 由未指定的 token 混合器(TokenMixer)和一个 MLP 块组成,可以表示为:
$$
X_{i+1} = MB_{i}(X_{i})=MLP(TokenMixer(X_{i}))
$$
其中,$X_{i|i>0}$ 是输入到第 $i$ 个 $MB$ 的中间特征。作者进一步将 Stage(或 S)定义为多个 MetaBlocks 的堆栈,这些 MetaBlocks 处理具有相同空间大小的特征,如上图中的 $N1×$ 表示 $S1$ 具有 $N1$ 个 MetaBlocks。该网络包括 4 个阶段。在每个阶段中,都有一个嵌入操作来投影嵌入维度和下采样 token 长度,如上图所示。在上述架构中,EfficientFormer 是一个完全基于 Transformer 的模型,无需集成 MobileNet 结构。接下来,作者深入研究了网络设计的细节。
Dimension-consistent Design
作者提出了一种维度一致性设计,该设计将网络分割为 4D 分区,其中操作符以卷积网络样式实现(MB4D),以及一个 3D 分区,其中线性投影和注意力在 3D 张量上执行,以在不牺牲效率的情况下享受 MHSA 的全局建模能力(MB3D),如上图所示。具体来说,网络从 4D 分区开始,而 3D 分区应用于最后阶段。注意,上图只是一个实例,4D 和 3D 分区的实际长度稍后通过架构搜索指定。
首先,输入图像由一个具有两个步长为 2,感受野为 3×3 卷积的 Conv stem 处理:
$$
X_{1}^{B,C_{j|j=1,\frac{H}{4},\frac{W}{4}}} = PatchEmbed(X_{0}^{B,3,H,W})
$$
其中,$C_{j}$ 是第 j 级的通道数量。然后,网络从 MB4D 开始,使用一个简单的池化混合器来提取低级特征:
$$
I_{i} = Pool(X_{i}{B,C,\frac{H}{2{j+1}},\frac{W}{2{j+1}}})+X_{i}{2{j+1}},\frac{W}{2{j+1}}}
$$
$$
X_{i+1}{B,C,\frac{H}{2{j+1}},\frac{W}{2^{j+1}}}=Conv_{B}(Conv_{B,G(I_{i}))}+I_{i}
$$
其中,$Conv_{B,G}$ 表示卷积后分别接 BN 和 GeLU。注意,这里作者没有在池化混合器之前使用 LN,因为 4D 分区是基于 CONV-BN 的设计,因此每个池化混合器前面都有一个 BN。
在处理完所有 MB4D 块后,作者执行一次 reshape 以变换特征大小并进入 3D 分区。MB3D 遵循传统 ViT 结构,如上图所示:
$$
I_{i} = Linear(MHSA(Linear(LN(X_{i}{B,\frac{HW}{4{j+1}},C_{j}}))))+X_{i}{B,\frac{HW}{4{j+1}},C_{j}}
$$
$$
X_{i+1}{B,\frac{HW}{4{j+1}},C_{j}} = Linear(Linear_{G}(LN(I_{i})))+I_{i}
$$
其中,$Linear_{G}$ 表示线性,后跟 GeLU。
$$
MHSA(Q,K,V) = Softamax(\frac{Q\odot K^{T}}{\sqrt{C_{j}}}). V
$$
其中 Q、K、V 表示通过线性投影学习的查询、键和值,b 表示作为位置编码的参数化注意力 bias。
#以 1x1 卷积为主的 MLP
class Mlp(nn.Module):
def __init__(self, in_features, hidden_features=None,
out_features=None, act_layer=nn.GELU, drop=0.):
super().__init__()
out_features = out_features or in_features
hidden_features = hidden_features or in_features
self.fc1 = nn.Conv2d(in_features, hidden_features, 1)
self.act = act_layer()
self.fc2 = nn.Conv2d(hidden_features, out_features, 1)
self.drop = nn.Dropout(drop)
self.apply(self._init_weights)
self.norm1 = nn.BatchNorm2d(hidden_features)
self.norm2 = nn.BatchNorm2d(out_features)
def _init_weights(self, m):
if isinstance(m, nn.Conv2d):
trunc_normal_(m.weight, std=.02)
if m.bias is not None:
nn.init.constant_(m.bias, 0)
def forward(self, x):
x = self.fc1(x)
x = self.norm1(x)
x = self.act(x)
x = self.drop(x)
x = self.fc2(x)
x = self.norm2(x)
x = self.drop(x)
return
class Meta4D(nn.Module):
def __init__(self, dim, pool_size=3, mlp_ratio=4.,
act_layer=nn.GELU,
drop=0., drop_path=0.,
use_layer_scale=True, layer_scale_init_value=1e-5):
super().__init__()
self.token_mixer = Pooling(pool_size=pool_size)
mlp_hidden_dim = int(dim * mlp_ratio)
#MLP 层
self.mlp = Mlp(in_features=dim, hidden_features=mlp_hidden_dim,
act_layer=act_layer, drop=drop)
#drop_path 目的是在一个 batch 里面随机去除一部分样本,起正则化作用
self.drop_path = DropPath(drop_path) if drop_path > 0. \
else nn.Identity()
self.use_layer_scale = use_layer_scale #可学习的参数,提供一个特征的缩放
if use_layer_scale:
self.layer_scale_1 = nn.Parameter(
layer_scale_init_value * torch.ones((dim)), requires_grad=True)
self.layer_scale_2 = nn.Parameter(
layer_scale_init_value * torch.ones((dim)), requires_grad=True)
def forward(self, x):
if self.use_layer_scale:
x = x + self.drop_path(
self.layer_scale_1.unsqueeze(-1).unsqueeze(-1)
* self.token_mixer(x))
x = x + self.drop_path(
self.layer_scale_2.unsqueeze(-1).unsqueeze(-1)
* self.mlp(x))
else:
x = x + self.drop_path(self.token_mixer(x))
x = x + self.drop_path(self.mlp(x))
return x
Latency Driven Slimming
Design of Supernet
基于维度一致性设计,作者构建了一个超网,用于搜索上图所示网络架构的有效模型(上图显示了搜索的最终网络的示例)。为了表示这样的超网,作者定义了元路径(MetaPath,MP),它是可能的块的集合:
$$
MP_{i,j=1,2} \in {MB_{i}^{4D},I_{i}}
$$
$$
MP_{i,j=3,4} \in {MB_{i}{4D},MB_{i},I_{i}}
$$
其中 $I$ 表示 identity path,$j$ 表示第 $j$ 阶段,$i$ 表示第 $i$ 个块。
在超网的 $S_{1}$ 和 $S_{2}$ 中,每个块可以从 MB4D 或 I 中选择,而在 $S_{3}$ 和 $S_{4}$ 中,块可以是 MB3D、MB4D 或 I。出于两个原因,作者仅在最后两个阶段启用 MB3D:首先,由于 MHSA 的计算相对于 token 长度呈二次增长,因此在早期阶段对其进行集成将大大增加计算成本。其次,将全局 MHSA 应用于最后阶段符合这样一种直觉,即网络的早期阶段捕获低级特征,而后期阶段学习长期依赖性。
#Meta3D 与 Meta4D 在 MLP 有不同,Meta3D 使用如下的 LinearMLP,主要以线性层为主
class LinearMlp(nn.Module):
""" MLP as used in Vision Transformer, MLP-Mixer and related networks
"""
def __init__(self, in_features, hidden_features=None, out_features=None, act_layer=nn.GELU, drop=0.):
super().__init__()
out_features = out_features or in_features
hidden_features = hidden_features or in_features
self.fc1 = nn.Linear(in_features, hidden_features)
self.act = act_layer()
self.drop1 = nn.Dropout(drop)
self.fc2 = nn.Linear(hidden_features, out_features)
self.drop2 = nn.Dropout(drop)
def forward(self, x):
x = self.fc1(x)
x = self.act(x)
x = self.drop1(x)
x = self.fc2(x)
x = self.drop2(x)
return x
class Meta3D(nn.Module):
def __init__(self, dim, mlp_ratio=4.,
act_layer=nn.GELU, norm_layer=nn.LayerNorm,
drop=0., drop_path=0.,
use_layer_scale=True, layer_scale_init_value=1e-5):
super().__init__()
self.norm1 = norm_layer(dim)
self.token_mixer = Attention(dim)
self.norm2 = norm_layer(dim)
mlp_hidden_dim = int(dim * mlp_ratio)
self.mlp = LinearMlp(in_features=dim, hidden_features=mlp_hidden_dim,
act_layer=act_layer, drop=drop)
self.drop_path = DropPath(drop_path) if drop_path > 0. \
else nn.Identity()
self.use_layer_scale = use_layer_scale
if use_layer_scale:
self.layer_scale_1 = nn.Parameter(
layer_scale_init_value * torch.ones((dim)), requires_grad=True)
self.layer_scale_2 = nn.Parameter(
layer_scale_init_value * torch.ones((dim)), requires_grad=True)
def forward(self, x):
if self.use_layer_scale:
x = x + self.drop_path(
self.layer_scale_1.unsqueeze(0).unsqueeze(0)
* self.token_mixer(self.norm1(x)))
x = x + self.drop_path(
self.layer_scale_2.unsqueeze(0).unsqueeze(0)
* self.mlp(self.norm2(x)))
else:
x = x + self.drop_path(self.token_mixer(self.norm1(x)))
x = x + self.drop_path(self.mlp(self.norm2(x)))
return x
Searching Space
本文的搜索空间包括 $C_{j}$(每个阶段的宽度)、$N_{j}$(每个阶段的块数,即深度)和最后个应用 MB3D 的块。
Searching Algorithm
以前的硬件感知网络搜索方法通常依赖于在搜索空间中部署每个候选对象的硬件来获得延迟,这非常耗时。在这项工作中,作者提出了一种简单、快速但有效的基于梯度的搜索算法,以获得只需训练一次超网的候选网络。该算法有三个主要步骤。
首先,作者使用 Gumble Softmax 采样对超网进行训练,以获得每个 MP 内块的重要性得分,可以表示为:
$$
X_{i+1} = \sum_{n} \frac{e{(a_{i}+\epsilon_{i}^{n})}/ \tau}{\sum_{n} e{(a_{i}+\epsilon_{i}^{n})}} . MP_{i,j}(X_{i})
$$
其中,α评估 MP 中每个块的重要性,因为它表示选择块的概率;$\epsilon ~U(0,1)$;τ是温度;n 代表 MP 中的块体类型,即对于 $S_{1}$ 和 $S_{2}$,$n\in{4D,I}$;对于 $S_{3}$ 和 $S_{4}$ ,。通过训练之后,以获得经过训练的权重和结构参数α。
其次,作者通过收集不同宽度(16 的倍数)的 MB4D 和 MB3D 的设备上延迟来构建延迟查找表。
最后,作者使用查找表在第一步通过延迟评估获得的超网上执行网络瘦身。典型的基于梯度的搜索算法仅选择α最大的块,这不符合本文的范围,因为它无法搜索宽度 $C_{j}$。事实上,构造一个多宽度的超网需要消耗显存,甚至是不现实的,因为在本文的设计中,每个 MP 都有几个分支。作者不在复杂的搜索空间上直接搜索,而是在单宽度超网上执行逐步瘦身,如下所示。
作者首先将 $S_{1,2}$ 和 $S_{3,4}$ 的 $MP_{i}$ 重要性得分分别定义为和 $\frac{α_{i}{4D}}{α_{i}{I}}$ 和 $\frac{α_{i}{3D}+α_{i}{4D}}{α_{i}^{I}}$。同样,每个阶段的重要性得分可以通过将该阶段内所有 MP 的得分相加得到。根据重要性得分,作者定义了包含三个选项的动作空间:1)选择 I 作为最小导入 MP,2)删除第一个 MB3D,3)减少最不重要阶段的宽度(乘以 16)。然后,通过查找表计算每个动作的延迟,并评估每个动作的准确度下降。最后,根据每延迟准确度下降 $(\frac{-%}{ms})$ 来选择操作。此过程将迭代执行,直到达到目标延迟。
EfficientFormer 一共有 4 个阶段。每个阶段都有一个 Embeding(两个 3x3 的 Conv 组成一个 Embeding)来投影 Token 长度(可以理解为 CNN 中的 feature map)。EfficientFormer 是一个完全基于 Transformer 设计的模型,并没有集成 MobileNet 相关内容。最后通过 AUTOML 来搜索 MB_3D 和 MB_4D block 相关参数。最后堆叠 block 形成最终网络。
EfficientFormer V2 模型
EfficientFormer V2:论文重新审视了 ViT 的设计选择,并提出了一种具有低延迟和高参数效率的改进型超网络。论文进一步引入了一种细粒度联合搜索策略,该策略可以通过同时优化延迟和参数量来找到有效的架构。所提出的模型 EfficientFormerV2 在 ImageNet-1K 上实现了比 MobileNetV2 和 MobileNetV1 高约 4%的 top-1 精度,具有相似的延迟和参数。
EfficientFormerV2 相对于 EfficientFormer 的主要改进如下图所示。
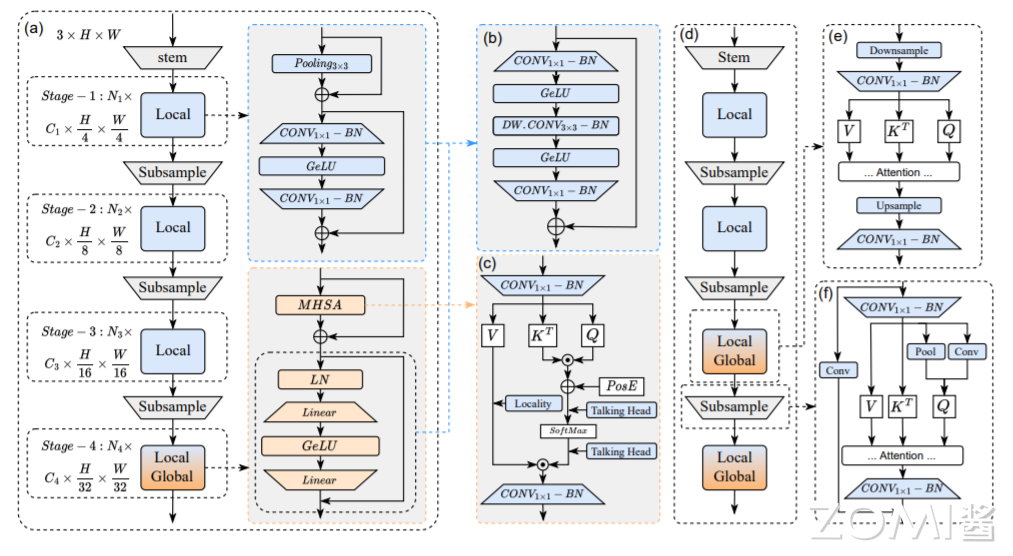
结合局部信息可以提高性能,并使 ViT 在缺少显式位置嵌入的情况下更加鲁棒。PoolFormer 和 EfficientFormer 使用 3×3 平均池化层(作为 local token 混合器。用相同内核大小的 depth-wise 卷积)替换这些层不会引入耗时开销,而使用可忽略的额外参数(0.02M),性能提高了 0.6%。此外。在 ViT 中的前馈网络(FFN)中注入局部信息建模层也有利于以较小的开销提高性能。值得注意的是,通过在 FFN 中放置额外的 depth-wise 3×3 卷积来捕获局部信息,复制了原始局部混合器(池或卷积)的功能。基于这些观察,论文移除了显式残差连接的 local token 混合器,并将 depth-wise 3×3 CONV 移动到 FFN 中,以获得 locality enabled 的统一 FFN(上图(b))。论文将统一的 FFN 应用于网络的所有阶段,如上图(a,b)所示。这种设计修改将网络架构简化为仅两种类型的 block(local FFN 和 global attention),并在相同的耗时(见表 1)下将精度提高到 80.3%,参数开销较小(0.1M)。更重要的是,该修改允许直接使用模块的确切数量搜索网络深度,以提取局部和全局信息,尤其是在网络的后期阶段。
| Method | #Params(M) | MACs(G) | Latency(ms) | Top-1(%) |
|---|---|---|---|---|
| EfficientFormer-L1 | 12.25 | 1.30 | 1.4 | 79.2 |
| Pool Mixer → $DWCONV_{3×3}$ | 12.27 | 1.30 | 1.4 | 79.8 |
| ✓ Feed Forward Network | 12.37 | 1.33 | 1.4 | 80.3 |
| ✓ Vary Depth and Width | 12.24 | 1.20 | 1.3 | 80.5 |
| 5-Stage Network | 12.63 | 1.08 | 1.5 | 80.3 |
| ✓ Locality in V & Talking Head | 12.25 | 1.21 | 1.3 | 80.8 |
| Attention at Higher Resolution | 13.10 | 1.48 | 3.5 | 81.7 |
| ✓ Stride Attention | 13.10 | 1.31 | 1.5 | 81.5 |
| ✓ Attention Downsampling | 12.40 | 1.35 | 1.6 | 81.8 |
搜索空间优化
通过统一的 FFN 和删除残差连接的 token mixer,V2 检查来自 EfficientFormer 的搜索空间是否仍然足够,特别是在深度方面。论文改变了网络深度(每个阶段中的 block 数)和宽度(通道数),并发现更深和更窄的网络会带来更好的精度(0.2%的改进)、更少的参数(0.3M 的减少)和更少的耗时(0.1ms 的加速),如上表所示。因此,论文将此网络设置为新的基线(精度 80.5%),以验证后续的设计修改,并为架构搜索提供更深入的超网络。
此外,具有进一步缩小的空间分辨率(1/64)的 5 阶段模型已广泛用于有效的 ViT 工作。为了证明是否应该从一个 5 阶段超网络中搜索,论文在当前的基线网络中添加了一个额外的阶段,并验证了性能增益和开销。值得注意的是,尽管考虑到小的特征分辨率,计算开销不是一个问题,但附加阶段是参数密集型的。因此需要缩小网络维度(深度或宽度),以将参数和延迟与基线模型对齐,以便进行公平比较。如上表所示,尽管节省了 MACs(0.12G),但 5 阶段模型的最佳性能在更多参数(0.39M)和延迟开销(0.2ms)的情况下意外降至 80.31%。这符合直觉,即五阶段计算效率高,但参数密集。鉴于 5 阶段网络无法在现有的规模和速度范围内引入更多潜力,论文坚持 4 阶段设计。这一分析也解释了为什么某些 ViT 在 MACs 精度方面提供了出色的 Pareto curve,但在大小上往往非常冗余。作为最重要的一点,优化单一度量很容易陷入困境。
# 深度卷积前馈网络(局部模块)
class FFN(nn.Module):
def __init__(self, dim, pool_size=3, mlp_ratio=4.,
act_layer=nn.GELU,
drop=0., drop_path=0.,
use_layer_scale=True, layer_scale_init_value=1e-5):
super().__init__()
mlp_hidden_dim = int(dim * mlp_ratio) # 隐藏层维度
self.mlp = Mlp(in_features=dim, hidden_features=mlp_hidden_dim,
act_layer=act_layer, drop=drop, mid_conv=True) # 多层感知机
self.drop_path = DropPath(drop_path) if drop_path > 0. \
else nn.Identity()
self.use_layer_scale = use_layer_scale
if use_layer_scale:
self.layer_scale_2 = nn.Parameter(
layer_scale_init_value * torch.ones(dim).unsqueeze(-1).unsqueeze(-1), requires_grad=True) # 缩放因子
def forward(self, x):
if self.use_layer_scale:
x = x + self.drop_path(self.layer_scale_2 * self.mlp(x)) # 残差连接
else:
x = x + self.drop_path(self.mlp(x))
return x
多头注意力改进
然后,论文研究了在不增加模型大小和耗时的额外开销的情况下提高注意力模块性能的技术。如图(c)所示,论文研究了 MHSA 的两种方法。首先通过添加 depth-wise 3×3 CONV 将局部信息注入到 Value 矩阵(V)中,也采用了这种方法。其次通过在 head 维度上添加全连接层来实现注意力头之间的通信,如图 2(c)所示。通过这些修改,进一步将性能提高到 80.8%,与基线模型相比,具有相似的参数和延迟。
class Attention4D(torch.nn.Module):
def __init__(self, dim=384, key_dim=32, num_heads=8,
attn_ratio=4,
resolution=7,
act_layer=nn.ReLU,
stride=None):
super().__init__()
self.num_heads = num_heads
self.scale = key_dim ** -0.5
self.key_dim = key_dim
self.nh_kd = nh_kd = key_dim * num_heads
if stride is not None:
self.resolution = math.ceil(resolution / stride)
self.stride_conv = nn.Sequential(nn.Conv2d(dim, dim, kernel_size=3, stride=stride, padding=1, groups=dim),
nn.BatchNorm2d(dim), )
self.upsample = nn.Upsample(scale_factor=stride, mode='bilinear')
else:
self.resolution = resolution
self.stride_conv = None
self.upsample = None
self.N = self.resolution ** 2
self.N2 = self.N
self.d = int(attn_ratio * key_dim)
self.dh = int(attn_ratio * key_dim) * num_heads
self.attn_ratio = attn_ratio
h = self.dh + nh_kd * 2
self.q = nn.Sequential(nn.Conv2d(dim, self.num_heads * self.key_dim, 1),
nn.BatchNorm2d(self.num_heads * self.key_dim), )
self.k = nn.Sequential(nn.Conv2d(dim, self.num_heads * self.key_dim, 1),
nn.BatchNorm2d(self.num_heads * self.key_dim), )
self.v = nn.Sequential(nn.Conv2d(dim, self.num_heads * self.d, 1),
nn.BatchNorm2d(self.num_heads * self.d),
)
self.v_local = nn.Sequential(nn.Conv2d(self.num_heads * self.d, self.num_heads * self.d,
kernel_size=3, stride=1, padding=1, groups=self.num_heads * self.d),
nn.BatchNorm2d(self.num_heads * self.d), )
self.talking_head1 = nn.Conv2d(self.num_heads, self.num_heads, kernel_size=1, stride=1, padding=0)
self.talking_head2 = nn.Conv2d(self.num_heads, self.num_heads, kernel_size=1, stride=1, padding=0)
self.proj = nn.Sequential(act_layer(),
nn.Conv2d(self.dh, dim, 1),
nn.BatchNorm2d(dim), )
points = list(itertools.product(range(self.resolution), range(self.resolution)))
N = len(points)
attention_offsets = {}
idxs = []
for p1 in points:
for p2 in points:
offset = (abs(p1[0] - p2[0]), abs(p1[1] - p2[1]))
if offset not in attention_offsets:
attention_offsets[offset] = len(attention_offsets)
idxs.append(attention_offsets[offset])
self.attention_biases = torch.nn.Parameter(
torch.zeros(num_heads, len(attention_offsets)))
self.register_buffer('attention_bias_idxs',
torch.LongTensor(idxs).view(N, N))
@torch.no_grad()
def train(self, mode=True):
super().train(mode)
if mode and hasattr(self, 'ab'):
del self.ab
else:
self.ab = self.attention_biases[:, self.attention_bias_idxs]
def forward(self, x): # x (B,N,C)
B, C, H, W = x.shape
if self.stride_conv is not None:
x = self.stride_conv(x)
q = self.q(x).flatten(2).reshape(B, self.num_heads, -1, self.N).permute(0, 1, 3, 2) # 降维为 2 维,转置
k = self.k(x).flatten(2).reshape(B, self.num_heads, -1, self.N).permute(0, 1, 2, 3)
v = self.v(x)
v_local = self.v_local(v) # 通过一个 3x3 的卷积将局部信息注入 V 中
v = v.flatten(2).reshape(B, self.num_heads, -1, self.N).permute(0, 1, 3, 2) # 降维为 2 维,转置
attn = (
(q @ k) * self.scale # 矩阵乘法,计算相似度
+
(self.attention_biases[:, self.attention_bias_idxs] # 融合一个位置编码
if self.training else self.ab)
)
# attn = (q @ k) * self.scale
attn = self.talking_head1(attn) # 1x1 卷积->全连接,实现注意力头部之间的通信
attn = attn.softmax(dim=-1)
attn = self.talking_head2(attn) # 同上
x = (attn @ v) # 注意力融合
out = x.transpose(2, 3).reshape(B, self.dh, self.resolution, self.resolution) + v_local # 最后再与 v_local 融合
if self.upsample is not None:
out = self.upsample(out)
out = self.proj(out) # 输出再进行激活 + 卷积 + 正则
return out
#AttnFFN(Local Global 模块)
class AttnFFN(nn.Module):
def __init__(self, dim, mlp_ratio=4.,
act_layer=nn.ReLU, norm_layer=nn.LayerNorm,
drop=0., drop_path=0.,
use_layer_scale=True, layer_scale_init_value=1e-5,
resolution=7, stride=None):
super().__init__()
self.token_mixer = Attention4D(dim, resolution=resolution, act_layer=act_layer, stride=stride) # MHSA 多头自注意力
mlp_hidden_dim = int(dim * mlp_ratio) # 隐藏层维度
self.mlp = Mlp(in_features=dim, hidden_features=mlp_hidden_dim,
act_layer=act_layer, drop=drop, mid_conv=True) # 深度卷积
self.drop_path = DropPath(drop_path) if drop_path > 0. \
else nn.Identity() # drop_path 概率
self.use_layer_scale = use_layer_scale
if use_layer_scale: # 缩放因子
self.layer_scale_1 = nn.Parameter(
layer_scale_init_value * torch.ones(dim).unsqueeze(-1).unsqueeze(-1), requires_grad=True)
self.layer_scale_2 = nn.Parameter(
layer_scale_init_value * torch.ones(dim).unsqueeze(-1).unsqueeze(-1), requires_grad=True)
def forward(self, x):
if self.use_layer_scale:
x = x + self.drop_path(self.layer_scale_1 * self.token_mixer(x)) # 多头自注意力 + 残差连接
x = x + self.drop_path(self.layer_scale_2 * self.mlp(x)) # mlp 深度卷积 + 残差连接
else:
x = x + self.drop_path(self.token_mixer(x))
x = x + self.drop_path(self.mlp(x))
return x
更高分辨率注意力
注意机制有利于性能。然而,将其应用于高分辨率特征会损害部署效率,因为它具有与空间分辨率相对应的二次时间复杂度。论文研究了将 MHSA 有效应用于更高分辨率(早期阶段)的策略。回想一下,在当前基线网络中,MHSA 仅在输入图像空间分辨率为 1/32 的最后阶段使用。论文将额外的 MHSA 应用于具有 1/16 特征大小的倒数第二个阶段,并观察到准确度提高了 0.9%。另一方面,推理速度减慢了几乎 2.7 倍。因此,有必要适当降低注意力模块的复杂性。
尽管一些工作提出了基于窗口的注意力,或下采样 Key 和 Value 来缓解这个问题,但论文发现它们不是最适合移动部署的选项。由于复杂的窗口划分和重新排序,基于窗口的注意力很难在移动设备上加速。对于[40]中的下采样 Key(K)和 Value(V),需要全分辨率查询(Q)来保持注意力矩阵乘法后的输出分辨率(Out):
$$
Out_{[B,H,N,C]} = (Q_{[B,H,N,C]}.K^{T}{[B,H,C,\frac{N}{2}]}).V,C]}\tag{1}
$$
根据测试该模型的耗时仅下降到 2.8ms,仍然比基线模型慢 2 倍。因此,为了在网络的早期阶段执行 MHSA,论文将所有 Query、Key 和 Value 降采样到固定的空间分辨率(1/32),并将注意力的输出插值回原始分辨率,以馈送到下一层,如图所示((d)和(e))。我们称这种方法为“Stride Attention”。如表所示,这种简单的近似值将延迟从 3.5ms 显著降低到 1.5ms,并保持了具有竞争力的准确性(81.5%对 81.7%)。
class Attention4DDownsample(torch.nn.Module):
def __init__(self, dim=384, key_dim=16, num_heads=8,
attn_ratio=4,
resolution=7,
out_dim=None,
act_layer=None,
):
super().__init__()
self.num_heads = num_heads
self.scale = key_dim ** -0.5
self.key_dim = key_dim
self.nh_kd = nh_kd = key_dim * num_heads
self.resolution = resolution
self.d = int(attn_ratio * key_dim)
self.dh = int(attn_ratio * key_dim) * num_heads
self.attn_ratio = attn_ratio
h = self.dh + nh_kd * 2
if out_dim is not None:
self.out_dim = out_dim
else:
self.out_dim = dim
self.resolution2 = math.ceil(self.resolution / 2)
self.q = LGQuery(dim, self.num_heads * self.key_dim, self.resolution, self.resolution2) # 双注意力下采样
self.N = self.resolution ** 2
self.N2 = self.resolution2 ** 2
self.k = nn.Sequential(nn.Conv2d(dim, self.num_heads * self.key_dim, 1),
nn.BatchNorm2d(self.num_heads * self.key_dim), )
self.v = nn.Sequential(nn.Conv2d(dim, self.num_heads * self.d, 1),
nn.BatchNorm2d(self.num_heads * self.d),
)
self.v_local = nn.Sequential(nn.Conv2d(self.num_heads * self.d, self.num_heads * self.d,
kernel_size=3, stride=2, padding=1, groups=self.num_heads * self.d),
nn.BatchNorm2d(self.num_heads * self.d), )
self.proj = nn.Sequential(
act_layer(),
nn.Conv2d(self.dh, self.out_dim, 1),
nn.BatchNorm2d(self.out_dim), )
points = list(itertools.product(range(self.resolution), range(self.resolution)))
points_ = list(itertools.product(
range(self.resolution2), range(self.resolution2)))
N = len(points)
N_ = len(points_)
attention_offsets = {}
idxs = []
for p1 in points_:
for p2 in points:
size = 1
offset = (
abs(p1[0] * math.ceil(self.resolution / self.resolution2) - p2[0] + (size - 1) / 2),
abs(p1[1] * math.ceil(self.resolution / self.resolution2) - p2[1] + (size - 1) / 2))
if offset not in attention_offsets:
attention_offsets[offset] = len(attention_offsets)
idxs.append(attention_offsets[offset])
self.register_buffer('attention_biases', torch.zeros(num_heads, 196))
self.register_buffer('attention_bias_idxs',
torch.ones(49, 196).long())
self.attention_biases_seg = torch.nn.Parameter(
torch.zeros(num_heads, len(attention_offsets)))
self.register_buffer('attention_bias_idxs_seg',
torch.LongTensor(idxs).view(N_, N))
@torch.no_grad()
def train(self, mode=True):
super().train(mode)
if mode and hasattr(self, 'ab'):
del self.ab
else:
self.ab = self.attention_biases_seg[:, self.attention_bias_idxs_seg]
def forward(self, x): # x (B,N,C)
B, C, H, W = x.shape
q = self.q(x).flatten(2).reshape(B, self.num_heads, -1, H * W // 4).permute(0, 1, 3, 2)
k = self.k(x).flatten(2).reshape(B, self.num_heads, -1, H * W).permute(0, 1, 2, 3)
v = self.v(x)
v_local = self.v_local(v)
v = v.flatten(2).reshape(B, self.num_heads, -1, H * W).permute(0, 1, 3, 2)
attn = (q @ k) * self.scale # (H * W // 4, H * W)
bias = self.attention_biases_seg[:, self.attention_bias_idxs_seg] if self.training else self.ab
bias = torch.nn.functional.interpolate(bias.unsqueeze(0), size=(attn.size(-2), attn.size(-1)), mode='bicubic')
attn = attn + bias
attn = attn.softmax(dim=-1)
x = (attn @ v).transpose(2, 3) # (H * W // 4, H * W)
out = x.reshape(B, self.dh, H // 2, W // 2) + v_local
out = self.proj(out)
return out
注意力降采样
大多数视觉主干利用跨步卷积或池化层来执行静态和局部下采样,并形成分层结构。最近的一些研究开始探索注意力下采样。例如,LeViT 和 UniNet 建议通过注意力机制将特征分辨率减半,以实现全局感受野的上下文感知下采样。具体而言,Query 中的 token 数量减少一半,以便对注意力模块的输出进行下采样:
$$
Out_{[B,H,\frac{N}{2},C]} = (Q_{[B,H,\frac{N}{2},C]}.K^{T}{[B,H,C,N]}).V\tag{2}
$$
然而,决定如何减少 Query 中的 token 数量是非常重要的。Graham 等人根据经验使用池化对 Query 进行下采样,而 Liu 等人建议搜索局部或全局方法。为了在移动设备上实现可接受的推理速度,将注意力下采样应用于具有高分辨率的早期阶段是不利的,这限制了以更高分辨率搜索不同下采样方法的现有工作的价值。
相反,论文提出了一种同时使用局部性和全局依赖性的组合策略,如图(f)所示。为了获得下采样的 Query,论文使用池化层作为静态局部下采样,使用 3×3 DWCONV 作为可学习的局部下采样。此外,注意力下采样模块残差连接到 regular strided CONV,以形成 local-global 方式,类似于下采样 bottlenecks 或 inverted bottlenecks。如表所示,通过略微增加参数和耗时开销,论文进一步将注意力下采样的准确率提高到 81.8%。
class LGQuery(torch.nn.Module):
def __init__(self, in_dim, out_dim, resolution1, resolution2):
super().__init__()
self.resolution1 = resolution1
self.resolution2 = resolution2
self.pool = nn.AvgPool2d(1, 2, 0)
self.local = nn.Sequential(nn.Conv2d(in_dim, in_dim, kernel_size=3, stride=2, padding=1, groups=in_dim),
)
self.proj = nn.Sequential(nn.Conv2d(in_dim, out_dim, 1),
nn.BatchNorm2d(out_dim), )
def forward(self, x):
B, C, H, W = x.shape
local_q = self.local(x)
pool_q = self.pool(x)
q = local_q + pool_q # 双路径下采
q = self.proj(q)
return q
模型设计
如前文所述,论文采用了四阶段分层设计,其获得的特征尺寸为输入分辨率的{1/4,1/8,1/16,1/32}。EfficientFormerV2 从一个小的内核卷积 stem 开始嵌入输入图像,而不是使用非重叠 patch 的低效嵌入,
$$
X_{i|i=1,j|j=1}^{B,C_{j|j=1},\frac{H}{4},\frac{W}{4}} = stem(X_{0}^{B,3,H,W}) \tag{3}
$$
前两个阶段捕获高分辨率的局部信息;因此论文只使用统一的 FFN(FFN,图(b)):
$$
X_{i+1,j}{B,C_{j},\frac{H}{2{j+1}},\frac{W}{2^{j+1}}} = S_{i,j}.FFN^{C_{j},E_{i,j}(X_{i,j})}+X_{i,j} \tag{4}
$$
在最后两个阶段,使用局部 FFN 和全局 MHSA 块。因此式 4,global blocks 定义为:
$$
X_{i+1,j}{B,C_{j},\frac{H}{2{j+1}},\frac{W}{2^{j+1}}} = S_{i,j}.MHSA(Proj(X_{i,j}))+X_{i,j} \tag{5}
$$
$$
MHSA(Q,K,V) = Softmax(Q.K^{T}+ab).V \tag{6}
$$
优化模型
尽管基线网络 EfficientFormer 是通过耗时驱动搜索发现的,并且在移动设备上具有快速的推理速度,但搜索算法有两个主要缺点。首先,搜索过程仅受速度限制,导致最终模型是参数冗余的,如图 1 所示。其次,它仅搜索深度(每个阶段的 blocks 数)和阶段宽度,这是一种粗粒度的方式。事实上,网络的大多数计算和参数都在 FFN 中,并且参数和计算复杂度与其扩展比线性相关。可以针对每个 FFN 独立地指定,而不必相同。因此,搜索实现了更细粒度的搜索空间,其中计算和参数可以在每个阶段内灵活且非均匀地分布。其中在每个阶段保持相同。论文提出了一种搜索算法,该算法实现了灵活的 per-block 配置,并对大小和速度进行了联合约束,并找到了最适合移动设备的视觉主干。
搜索目标
首先,论文介绍了指导联合搜索算法的度量。考虑到在评估移动友好模型时网络的大小和延迟都很重要,我们考虑了一个通用的、公平的度量标准,它可以更好地理解移动设备上网络的性能。在不失一般性的情况下,我们定义了 Mobile Efficiency Score(MES):
$$
MES = Score.\prod_{i=1}(\frac{M_{i}}{U_{i}})^{\alpha_{i}}\tag{7}
$$
分数是为简单起见设置为 100 的预定义基础分数。模型大小是通过参数的数量来计算的,延迟是在设备上部署模型时的运行时间。论文在 MES 精度上搜索 Pareto optimality。MES 的形式是通用的,可以扩展到其他感兴趣的度量,例如推理时间内存占用和能耗。此外,通过适当定义,可以轻松调整每个度量的重要性。
搜索空间和 SuperNet
搜索空间组成:
网络的深度,由每个阶段的 blocks 数测量;
网络的宽度,即每阶段的通道维度;
每个 FFN 的膨胀率。
MHSA 的数量可以在深度搜索期间无缝地确定,这控制了超网络中 block 的保存或删除。因此,论文在超网络的最后两个阶段将每个 block 设置为 MHSA,然后是 FFN,并通过深度搜索获得具有所需数量的全局 MHSA 的子网络。
SuperNet 是通过使用在弹性深度和宽度上执行的可精简网络[78]来构建的,以实现纯基于评估的搜索算法。弹性深度可以通过 stochastic drop path augmentation 实现[32]。关于宽度和扩展比,论文遵循 Yu 等人[78]构建具有共享权重但独立规正则化层的可切换层,使得相应层可以在预定义集合的不同通道数量上(即 16 或 32 的倍数)执行。具体而言,膨胀比由每个 FFN 中的 depth-wise 3×3 Conv 的通道确定,并且 stage 宽度通过对齐 FFN 和 MHSA block 的最后投影(1×1 Conv)的输出通道确定。可切换执行可以表示为:
$$
\hat{X_{i}} = γ_{c}.\frac{w{c}.X_{i}-u_{c}}{\sqrt{σ_{c}+ϵ}}+β_{c} \tag{8}
$$
通过在每次迭代中训练最大、最小和随机采样的两个子网(论文在算法 1 中将这些子网表示为 max、min、rand-1 和 rand-2),使用 Sandwich Rule 对超网络进行预训练。
搜索算法
现在,搜索目标、搜索空间和超网络集合都已公式化,论文提出了搜索算法。由于超网络在弹性深度和可切换宽度下可执行,论文可以通过分析每个效率增益和精度下降来搜索具有最佳 Pareto 曲线的子网络。行动池定义为:
$$
A\in{A_{N[i,j]},A_{C[j]},A_{E[i,j]}} \tag{9}
$$
使用全深度和全宽度(最大子网)初始化状态,论文评估 ImageNet-1K 验证集上每个前沿操作的精度结果,这只需要大约 4 GPU 分钟。同时,参数缩减可以直接从层属性(即 kernel 大小、输入通道和输出通道)计算。论文通过使用 CoreMLTools 在 iPhone 12 上测量的预先构建的耗时查找表来获得耗时减少。有了这些度量就可以通过和计算,并选择每个 MES 精度下降最小的动作。值得注意的是,尽管动作组合非常庞大,但只需要在每个 step 评估前,这在复杂性上是线性的。
网络结构
对于模型大小,EfficientFormerV 2-S0 比 EdgeViT-XXS 超出了 1.3%的 top-1 精度,甚至少了 0.6M 参数,比 MobileNetV 2 ×1.0 优于 3.5%的 top-1,参数数量相似。对于大模型,EfficientFormerV 2-L 模型实现了与最近的 EfficientFormerL 7 相同的精度,同时小 3.1 倍。在速度方面,在延迟相当或更低的情况下,EfficientFormerV2-S2 的性能分别优于 UniNet-B1,EdgeViT-S 和 EfficientFormerL 1,分别为 0.8%,0.6%和 2.4%。EiffcientFormer V2-S1 的效率分别比 MobileViT-XS、EdgeViT-XXS 和 EdgeViTXS 高出 4.2%、4.6%和 1.5%,其中 MES 要高得多。
如果您想了解更多AI知识,与AI专业人士交流,请立即访问昇腾社区官方网站https://www.hiascend.com/或者深入研读《AI系统:原理与架构》一书,这里汇聚了海量的AI学习资源和实践课程,为您的AI技术成长提供强劲动力。不仅如此,您还有机会投身于全国昇腾AI创新大赛和昇腾AI开发者创享日等盛事,发现AI世界的无限奥秘~
转载自:https://www.cnblogs.com/ZOMI/articles/18561202


 浙公网安备 33010602011771号
浙公网安备 33010602011771号