M2 数据结构简略知识点
目录
1 常见的数据结构
1-1 Hash以及冲突解决方法
基本概念
- 散列函数:将关键字映射位地址(数组下标,索引,内存地址)的函数
- 冲突:不同关键字映射到同一地址
- 散列表:根据关键字进行查找的函数
散列函数的设计方法:
- 直接定址方法
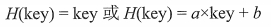
- 除留余数法(质数p的选取要根据散列表的长度确定)
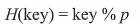
- 数字分析法
- 平方取中法
散列冲突的解决方式:
方式1:开放地址法(缺点:删除比较困难)
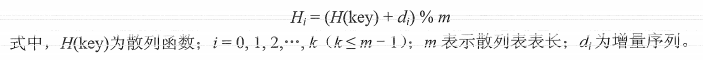
根据增量序列的确定策略细分为:
- 线性探测法(缺点:有堆积现象,查找效率会降低)

- 平方探测法(优点:避免堆积现象。缺点:不能探测表中所有位置)

- 再散列法(结合了上述两种方法优点,i是冲突次数)
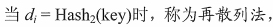
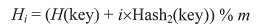
方式2:拉链法
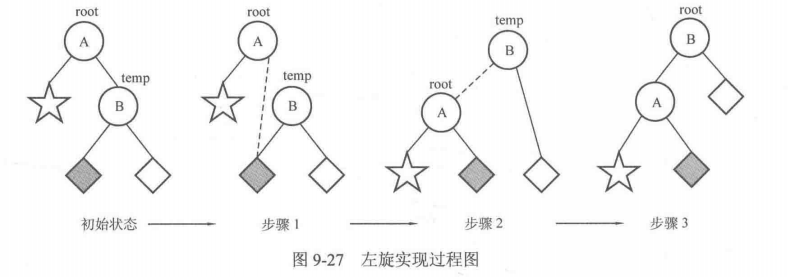
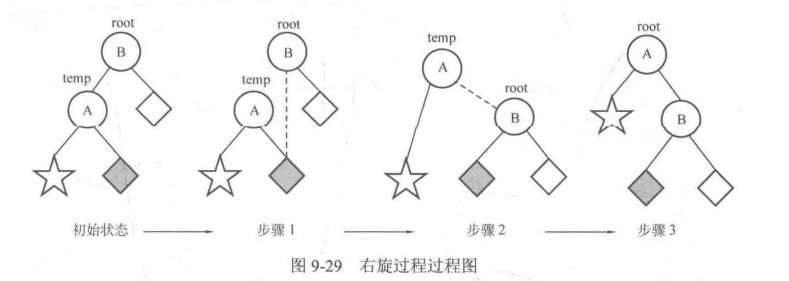
1-2 BST与AVL树与红黑树的常识
BST定义:左子树小于等于根节点,右子树大于等于根节点
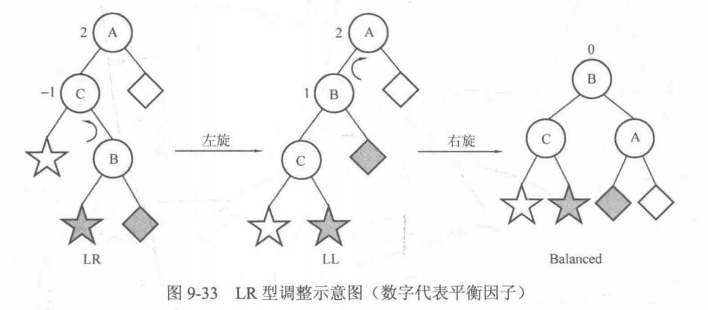
AVL树: 左右子树高度差不超过1的BST。
- 应用:实际中用的不是很多,


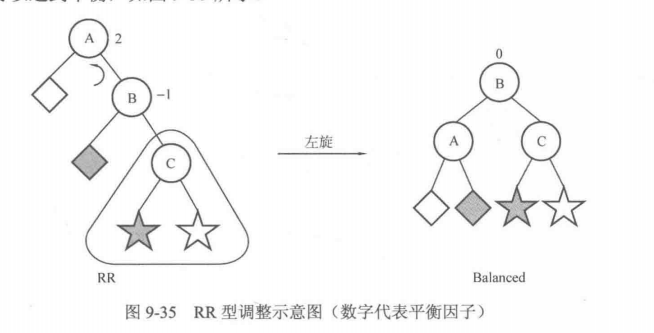

1-3 红黑树
特点:
- 一种平衡二叉树,但每个节点有一个存储位表示节点的颜色,可以是红或黑。红黑树确保没有一条路径会比其它路径长出两倍,因此,红黑树是一种弱平衡二叉树(由于是弱平衡,可以看到,在相同的节点情况下,AVL树的高度<=红黑树),相对于要求严格的AVL树来说,它的旋转次数少,所以对于搜索,插入,删除操作较多的情况下,用红黑树。
- 红黑树能够以 O(log n) 的时间复杂度进行搜索、插入、删除操作。此外,由于它的设计,任何不平衡都会在三次旋转之内解决。当然,还有一些更好的,但实现起来更复杂的数据结构,能够做到一步旋转之内达到平衡,但红黑树能够给我们一个比较“便宜”的解决方案。 红黑树的算法时间复杂度和AVL相同,但统计性能比AVL树更高。
- 一棵有 n 个内结点的红黑树的高度至多是 2log(n+1),只需要证明它的逆否命题高度为h的红黑树,节点个数最少是2^(h/2)-1;
具体性质:
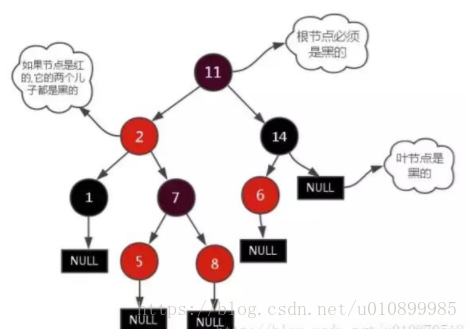

应用:
- 广泛用于C ++的STL中,map是用红黑树实现的;
- Linux的的进程调度,用红黑树管理进程控制块,进程的虚拟内存空间都存储在一颗红黑树上,每个虚拟内存空间都对应红黑树的一个节点,左指针指向相邻的虚拟内存空间,右指针指向相邻的高地址虚拟内存空间;
- IO多路复用的epoll采用红黑树组织管理sockfd,以支持快速的增删改查;
- Nginx中用红黑树管理定时器,因为红黑树是有序的,可以很快的得到距离当前最小的定时器;
- Java的TreeMap的实现;
1-4 哈夫曼编码基础概念
叶子节点的带权路径长度:叶子节点的值*路径长度
树的带权路径长度:所有叶子节点的带权路径长度之和。
1-5 跳表的实现
-
跳表通过抛硬币的方式维护上层节点数目是下层节点数数目的一半
- 元素X插入第n层的概率是(1/2)的n次。
-
跳表是一种动态数据结构,支持快速的插入删除查找操作,时间复杂度都是O(logn).
2 排序算法总览
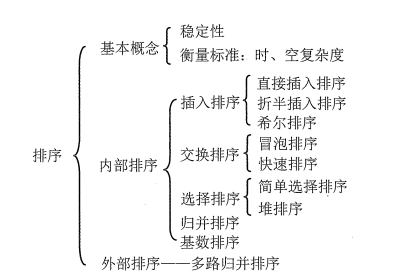

排序算法时间复杂度汇总

具体的实现
参考资料
- 王道数据结构

 1)hash表以及常见的查找结构 2)排序算法整体概述
1)hash表以及常见的查找结构 2)排序算法整体概述


 浙公网安备 33010602011771号
浙公网安备 33010602011771号