201971010139-汤可意 实验二 个人项目—《{0,1}背包问题》项目报告
【keyi21】软件工程准备报告[实验二]
201971010139-汤可意 实验二 个人项目—《{0,1}背包问题》项目报告
| 项目 | 内容 |
|---|---|
| 课程班级博客链接 | https://edu.cnblogs.com/campus/xbsf/2019nwnucs |
| 作业要求链接 | https://edu.cnblogs.com/campus/xbsf/2019nwnucs/homework/12527 |
| 我的课程学习目标 | 1.注册使用博客园并学习使用Markdown编辑器发表作业博客; 2.了解“提问”流程,学习“提问”方法; 3.学习并理解软件工程,顺利完成软件工程项目试验。 |
| 这个作业在哪些方面帮助我实现学习目标 | 1.完成博客园以及github用户注册; 2.学习并锻炼使用Markdown编辑器编写随笔发表博客; 3.初步学习排版设计; |
| 项目Github的仓库链接地址 | 201971010138-keyi21 |
·任务一
| 地址 | 评论 |
|---|---|
| 201971010142-王玉慧 实验一 软件工程准备—走进软件工程 | 行文完整条理清晰,尤其是用了很多隐藏超链接,使文章内容更加浓缩简练,值得学习 |
| 201971010111-何晨泽 实验二 个人项目—《{0-1}KP问题》项目报告 | 叹为观止,太强啦。 无论是项目完成度还是博文逻辑和观赏性,以我的水平完全没办法挑出毛病来.没法速成达到作者的编程水平,也可以学习博文排版和行动力.观摩一些六边形战士 |
| 201971010140-魏瑾川 实验一 软件工程准备—软件工程的第一印象 | 作者博客外观设计精美,内容完善丰满,排版美观易看,值得学习(看板娘好可爱 |
·任务二 总结详细阅读《构建之法》第1章、第2章,掌握PSP流程
1.第一章:什么是软件工程?
- 软件工程的定义
软件=程序+软件工程: - 软件工程的特点:
软件工程的特殊性:复杂性,不可见性,易变性,服从性,非连续性;
软件工程的知识领域、软件工程的三大类基础知识领域:计算基础,数学基础和工程基础;
软件工程的目标:用户满意度,可靠性,软件流程的质量,可维护性。
2.第二章: 主要讲解了PSP,即Personal Software Process,个人软件开发流程
“卡内基梅隆大学(CMU)的能力成熟度模型(CMM和CMMI),是用来衡量一个团队能力的一套模型。CMU的专家们针对软件工程师也有一套模型,叫Personal Software Process(PSP),PSP和任何其他方法论一样,也不是一蹴而就的。”
摘录来自: 邹欣. “构建之法:现代软件工程。” Apple Books.
- PSP特点:
- 不局限于某一种软件技术,而是着眼于软件开发的流程。
- 不依赖于考试,而是依赖工程师自己收集数据,然后分析,提高。
- 依赖于数据
- PSP作用:
- PSP可以帮助软件工程师在个人的基础上运用过程的原则,借助于PSP提供的一些度量和分析工具,了解自己的技能水平,控制和管理自己的工作方式,使自己日常工作的评估、计划和预测更加准确、更加有效,进而改进个人的工作表现,提高个人的工作质量和产量,积极而有效地参与高级管理人员和过程人员推动的组织范围的软件工程过程改进。
- 本项目PSP规划及总结:
见项目最后。
·任务三 项目开发
1.项目背景
背包问题(Knapsack Problem,KP)是NP Complete问题,也是一个经典的组合优化问题,有着广泛而重要的应用背景。{0-1}背包问题({0-1 }Knapsack Problem,{0-1}KP)是最基本的KP问题形式,它的一般描述为:从若干具有价值系数与重量系数的物品(或项)中,选择若干个装入一个具有载重限制的背包,如何选择才能使装入物品的重量系数之和在不超过背包载重前提下价值系数之和达到最大?
2.需求分析:
{0-1}KP数据集是研究{0-1}背包问题时,用于评测和观察设计算法性能的标准数据集;动态规划算法、回溯算法是求解{0-1}背包问题的经典算法。查阅相关资料,设计一个采用贪心算法、动态规划算法、回溯算法求解{0-1}背包问题的程序
- 程序基本功能要求如下:
- 数据输入输出:可正确读入实验数据文件的有效{0-1}KP数据;
- 散点图绘制:能够绘制任意一组{0-1}KP数据以价值重量为横轴、价值为纵轴的数据散点图;
- 排序:能够对一组{0-1}KP数据按重量比进行非递增排序;
- 算法选择:用户能够自主选择算法求解指定{0-1} KP数据的最优解和求解时间(以秒为单位),可选算法:
- 贪心算法;
- 动态规划算法;
- 回溯算法;
- 数据导出:任意一组{0-1} KP数据的最优解、求解时间和解向量可保存为txt文件或导出EXCEL文件。
3.功能设计:
- 使用工具
| 工具 | 介绍 |
|---|---|
| Xcode | 运行在操作系统Mac OS X上的集成开发工具(IDE),由Apple Inc开发。本项目的功能实现经由Xcode编译C++语言实现 |
| IntelliJ IDEA | 是java编程语言开发的集成环境,本项目的可视化实现由此完成 |
-
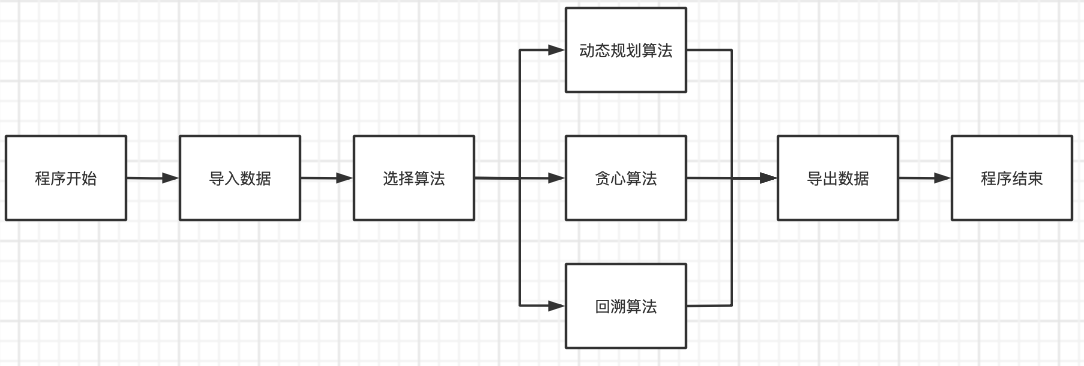
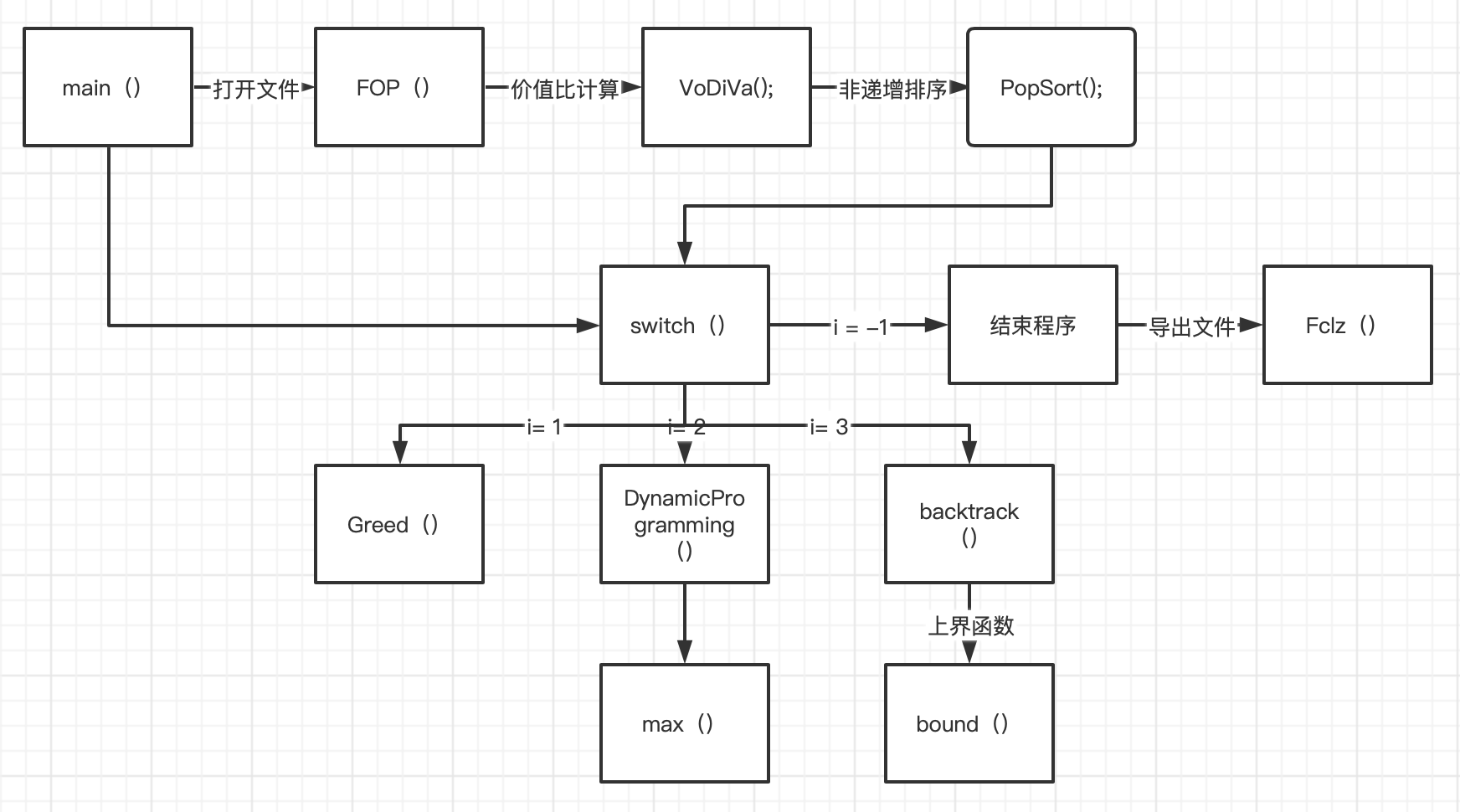
根据需求分析,本工程项目需实现从数据输入到输出的以下流程:
![]()
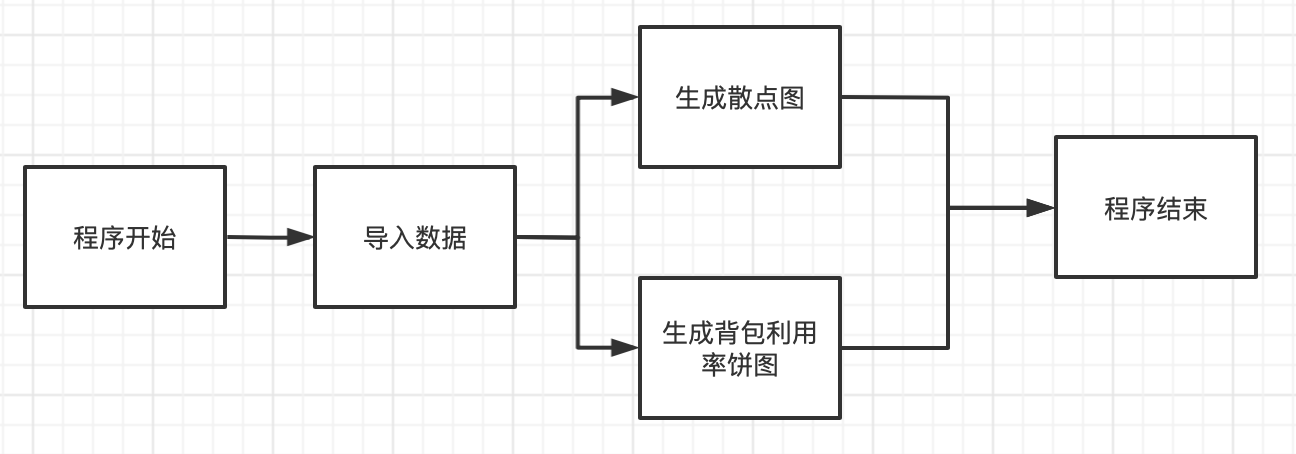
在可视化方面,本项目需要实现文件的读入到结束的以下流程:
![]()
-
函数设计以及相关联动:
-
main():程序主函数;
-
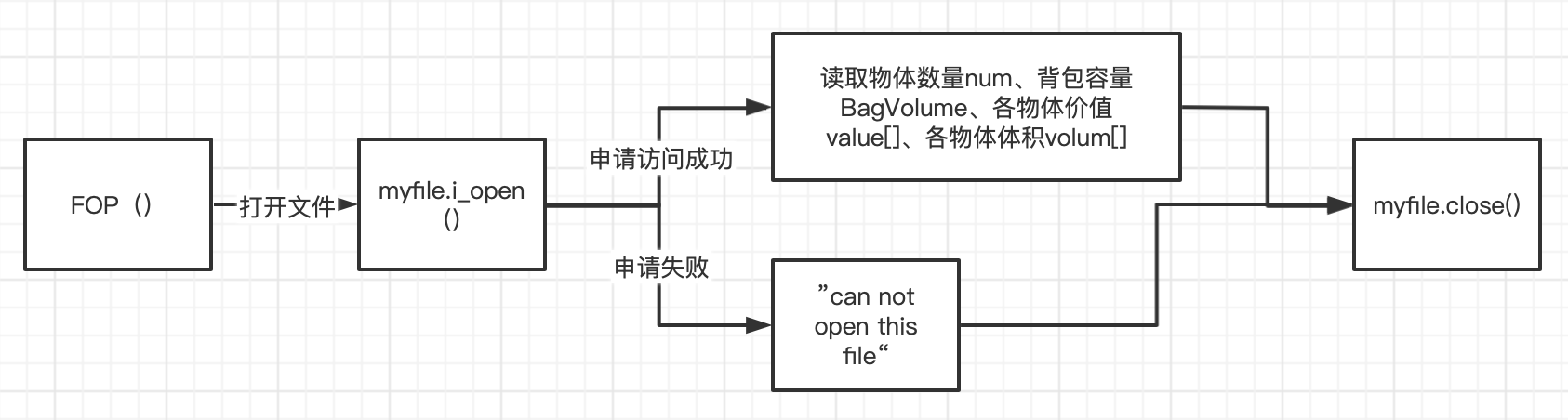
FOP():将存储数据的txt文件打开并导出数据;
![]()
-
VoDiVa():计算物品单位体积价值;
-
PopSort():将物体单位体积价值连同编号进行排序,需要VoDiVa()函数运行结束得到存储价值比的数组Sort[ ];
-
switch():对算法进行选择,输入-1时退出程序。可选择的算法有:
- Greed():贪心算法,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,算法得到的是在某种意义上的局部最优解。
- DynamicProgramming():动态规划算法,如果一类活动过程可以分为若干个互相联系的阶段,在每一个阶段都需作出决策(采取措施),一个阶段的决策确定以后,常常影响到下一个阶段的决策,从而就完全确定了一个过程的活动路线,则称它为多阶段决策问题。
- backtrack():回溯算法,类似枚举的搜索尝试过程,主要是在搜索尝试过程中寻找问题的解,当发现已不满足求解条件时,就“回溯”返回,尝试别的路径;
-
FCLZ():将结果导出到out.txt。
![]()
-
4.测试运行
-
从文件中读取数据
同意访问文件
![]()
![]()
-
对物品价值进行非递增排序
![]()
-
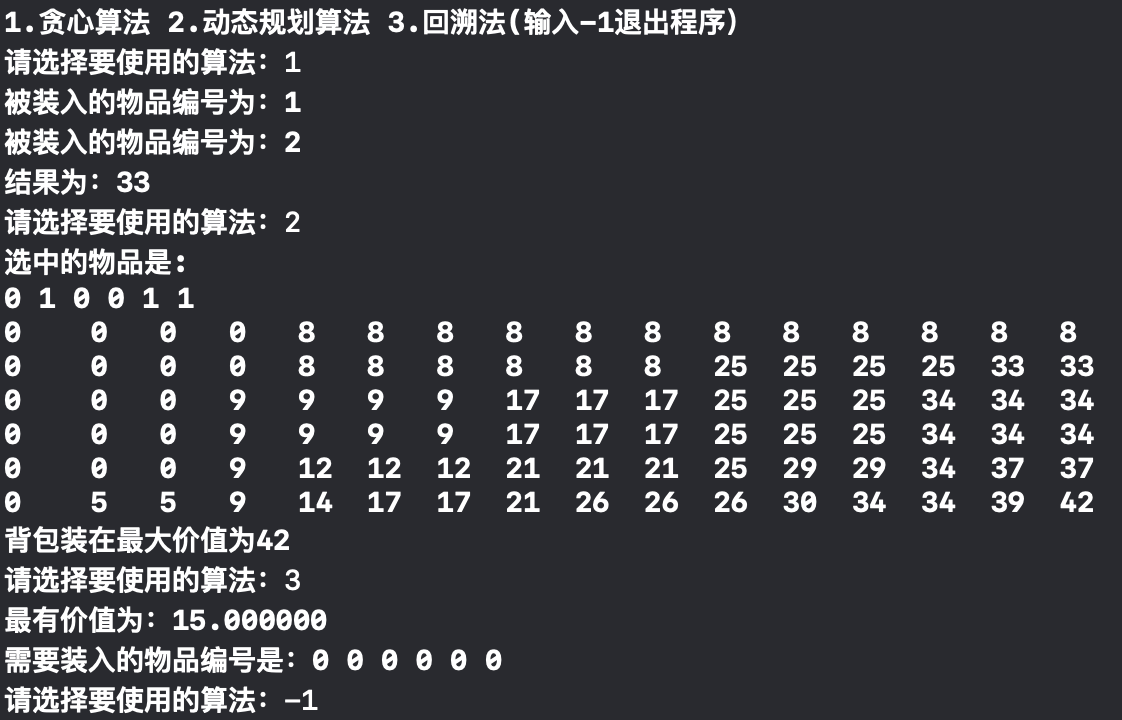
选择不同的算法进行实现
![]()
5.代码规范:
| 项目 | 规则 |
|---|---|
| 缩进 | 使用 𝑡𝑎𝑏 作为缩进 |
| 变量命名 | 1. 均不能以下划线开始,也不能以下划线结束 2. 禁止英文与拼音混用,仅允许纯拼音或纯英文 3. 采用类驼峰形式,命名首字母可小写,如 getMaxWeight 或 WriteFile 4. 允许单个小写英文字母的命名5. 允许纯大写英文字母的命名 |
| 每行最多字符数 | 单行字符数限制不超过256个 |
| 函数最大行数 | 单个函数行数限制不超过120行 |
| 函数、类命名 | 1. 均不能以下划线开始,也不能以下划线结束 2. 禁止英文与拼音混用,仅允许纯拼音或纯英文 3. 采用类驼峰形式,命名首字母可小写,如 getMaxWeight 或 WriteFile 4. 允许纯大写英文字母的命名 |
| 常量 | 同变量命名规则 |
| 空行规则 | 1. 引入头文件其间部分不允许空行 2. 静态变量/常量定义后跟一空行 3. 每个函数后跟一空行,除非是最后一个函数 4. 若函数为空,中间包含一空行 5. 其余除为了代码美观的空行,均不允许空行出现 |
| 注释规则 | 1. 行内注释可使用//...形式 2. 函数前部注释需使用/*内容/形式 |
| 操作符前后空格 | 1. if/for/while/switch/do等保留字与左右括号之间都必须加空格 2. 其余运算符左右均不加空格 |
| 其他规则 | 1. 左大括号前不换行 2. 右大括号前换行 |
6.核心代码展示说明:
- 贪心算法
//贪心算法
void Greed()
{
float temp=0;
float result=0;
float bv=BagVolume;
for(int i=0;i<num;i++)
{
//寻找最高价值的物品
for(i=0;i<num;i++){
if(temp<sortBest[i])
temp=sortBest[i];
}
//将最高价值的物品装入背包
for(i=0;i<num;i++){
if (temp==sortBest[i]){
sortBest[i]=0;
}
if (volume[i]<=bv){
result=result+value[i];
cout<<"被装入的物品编号为:"<<i+1<<endl;
}
bv=bv-volume[i];
}
}
cout<<"结果为:"<<result<<endl;
}
-
动态规划算法
int DynamicProgramming()
{int i, j; for (i = 0; i <= num; i++) V[i][0] = 0; for (j = 0; j <= BagVolume; j++) V[0][j] = 0; for (i = 0; i < num; i++){ for (j = 0; j < BagVolume+1; j++){ if (j<volume[i]) V[i][j] = V[i - 1][j]; else V[i][j] = max(V[i - 1][j], V[i - 1][j - volume[i]] + value[i]); } } j = BagVolume; for (i = num - 1; i >= 0; i--) { if (V[i][j]>V[i - 1][j]) { item[i] = 1; j = j - volume[i]; } else item[i] = 0; } printf("选中的物品是:\n"); for (i = 0; i<num; i++) printf("%d ", item[i]); printf("\n"); for (int i = 0; i < num; i++){ for (int j = 0; j < BagVolume+1; j++){ printf("%d\t ", V[i][j]); if (j == BagVolume){ printf("\n"); } } } printf("背包装在最大价值为%d\n", V[num - 1][BagVolume]); //system("pause"); return 0 ;}
-
回溯法
void backtrack(int i)
{double bound(int i); if(i>num) { bestp = BagVolume; return; } if(bagnow+volume[i]<=BagVolume) { bagnow+=volume[i]; bagvalue+=value[i]; put[i]=1; backtrack(i+1); bagnow-=volume[i]; bagvalue-=value[i]; } if(bound(i+1)>bestp)//符合条件搜索右子数 backtrack(i+1);}
7.总结
本项目使用C++和java两种不同的语言共同完成,由于本人水平有限,完成度尽我所能只有如此。
在完成实验的过程中,使用函数将将不同应用的代码分装起来,并设置全局变量,使之间可以相互调用,对提升代码的简洁性以及项目的易读性等方面都非常有效。
8.本项目所使用的PSP
| PSP2.1 | 任务内容 | 计划共完成需要的时间(min) | 实际完成需要的时间(min) |
|---|---|---|---|
| Planning | 计划 | 6 | 8 |
| - Estimate | - 估计这个任务需要多少时间,并规划大致工作步骤 | 6 | 8 |
| Development | 开发 | 510 | 600 |
| - Analysis | - 需求分析(包括学习新技术) | 10 | 6 |
| - Design Spec | - 生产设计文档 | 10 | 8 |
| - Design Review | - 设计复审(和同事审核设计文档) | 5 | 6 |
| - Coding Standard | - 代码规范(为目前的开发指定合适的规范) | 10 | 20 |
| - Design | - 具体设计 | 25 | 30 |
| - Coding | - 具体编码 | 500 | 600 |
| - Code Review | - 代码复审 | 30 | 30 |
| - Test | - 测试(自我测试,修改代码,提交修改) | 120 | 200 |
| Reporting | 报告 | 60 | 62 |
| - Test Report | - 测试报告 | 30 | 25 |
| - Size Measurement | - 计算工作量 | 10 | 13 |
| - Postmortem & Process Improvement Plan | - 事后总结,并提出过程改进计划 | 20 | 24 |
·任务四 Github的使用
将项目上传到Github中
本项目共使用commit11次。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号