红黑树

红黑树，除了符合二叉搜索树的基本规则外，还添加了一个特性：

1、节点是红色或黑色

2、根节点是黑色

3、每个叶子节点都是黑色的空节点（NIL节点）

4、每个红色节点的两个子节点都是黑色的，（从每个叶子到根的所有路径上不能有两个连续的红色节点）

5、从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点

 

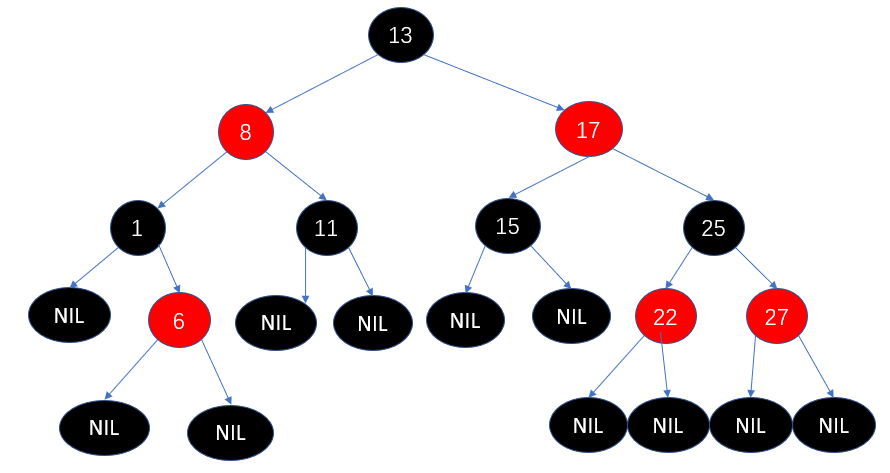
红黑树的相对平衡

红黑树的关键特性：从根到叶子的最长可能路径，不会超过最短可能路径的两倍长，结果就是这个树基本是平衡的

为什么可以做到最长路径不超过最短路径的两倍呢？

性质四决定了路径不能有两个相连的红色节点

最短的可能路径都是黑色节点

最长的可能路径是红色和黑色交替

性质五所有路径都有相同数据黑色节点

这就表明了没有路径能多余任何其他路径的两倍长

变色

插入一个新节点时，有可能树不在平衡，可以通过三种方式的变换，让树保持平衡：换色、左旋转、右旋转

变色：为了重新符合红黑树的规则，尝试把红色节点变为黑色，或者把黑色节点变为红色

首先，新插入的新节点通常都是红色节点，因为在插入节点为红色的时候，有可能插入一次是不违反红黑树任何规则的，而插入黑色节点，必然会导致有一条路径上多了黑色节点，这是很难调整的，红色节点可能导致出现红红相连的情况，但是这种情况可以通过颜色调换和旋转来调整

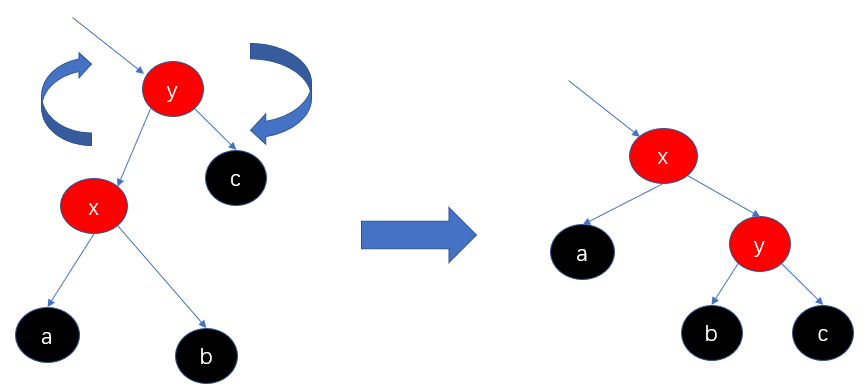
左旋转：逆时针旋转红黑树的两个节点，使得父节点被自己的右孩子取代，而自己成为自己的左孩子

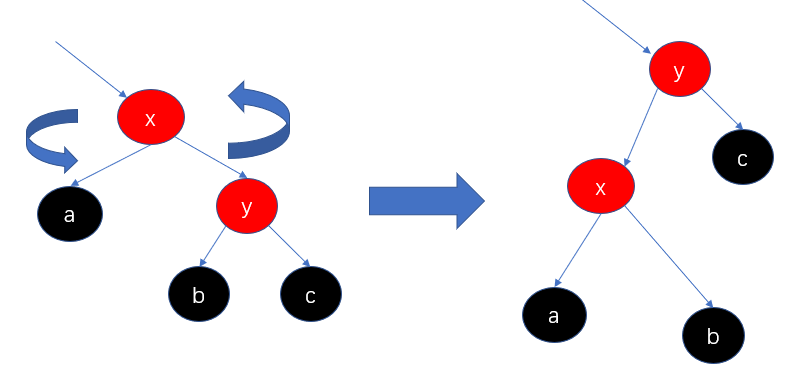
 右旋转：顺时针旋转红黑树的两个节点，使得父节点被自己的左孩子取代，而自己成为自己的右孩子