哈希表
哈希表是什么
哈希表通常是基于数组进行实现的,但是相对于数组有一下优势:
- 可以提供非常快速的插入-删除-查找操作
- 无论多少数据,插入和删除值需要接近常量的时候:即O(1)的时间级,实际上只需要几个机器指令即可完成
- 哈希表的速度比树还要快,基本可以瞬间查找到想要的元素
- 哈希表相对于树来说编码要容易很多
哈希表的结构:它的结构就是数组,但是它的神奇之处在于对下标值的一种变换,这种变换称为哈希函数,通过哈希函数可以得到HashCode
哈希化:将大数字转换成数组范围内下标的过程,称之为哈希化
哈希函数:通常我们会将单词转换成大数字,大数字在进行哈希化的代码实现放在一个函数中,这个函数称为哈希函数
哈希表:最终将数据插入到的额这个数组,对整个结构的封装就称为哈希表
什么是冲突?
数字转换成数组范围内下标的时候可能会导致下标重复,也就是冲突。
比如说我们需要存储50个单词,使用100个位置来存储,并且通过一种相对比较好的哈希函数来完成,但是依然可能会有冲突的可能,冲突不可避免,但是可以避免
解决冲突的办法有两种:
链地址法(拉链法)解决冲突的办法是每个数组单元中存储的不再是单个数据,而是一个链条,这个链条常见的是数组或者是链表
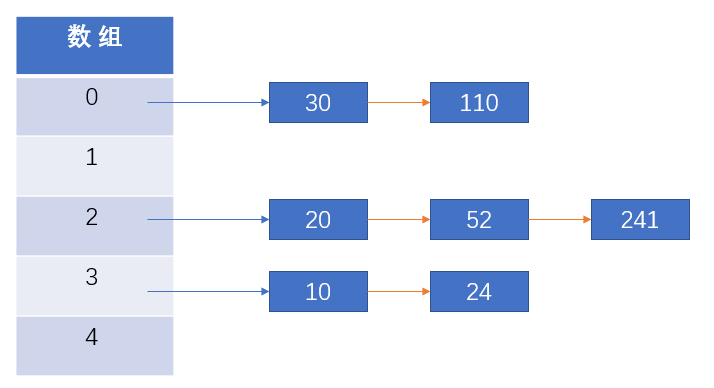
开放地址法的主要工作方式是寻找空白的单元格来添加重复的数据,主要有三种方法进行探索位置:线性探测、二次探测、再哈希法

线性探测:
比如说要插入的数据为18,经过哈希化之后index=1,但是index=1的位置上已经放着数据50了,就需要index位置加一,一点一点的查找合适的位置来防止18,空的位置就是合适的位置。
如果是查找的话,首先经过哈希化等到index=2,如果2的位置结果和查询的数值是一样的,那么久返回,如果不一样,就index加一,一点一点的查找,如果遇到空位置,就停止查找,因为找的这个数值是不会跳过空位置插入到其他位置的。
如果需要删除数据项的时候,不可以将这个数据项的下标的内容设置为null。因为将它设置为null可能会影响我们之后查询其他操作,所以通常删除一个位置的数据项时,将它进行特殊处理,比如设置为-1。
线性探测的问题:
线性探测有一个严重的问题,就是聚集,比如在没有任何人数据的时候,插入的是1-2-3-4-5,那么意味着下标值为0-1-2-3-4的位置都有元素,这种一连串田填充单元就叫做聚集,聚集会影响哈希表的性能,插入、查询、删除都会有影响,比如要插入数据12,会发现连续的单元都不允许插入数据,并且在这个过程中,我们需要探索多次,使用二次探测可以解决这个问题。
二次探测:
二次探测主要优化的是探测时的步长,线性探测是从步长为1开始探测(x+1,x+2,x+3依次探测),二次探测对步长做了优化(x+12,x+22,x+33),这样一次可以探测比较长的距离,避免聚集带来的影响。
二次探测的影响:
比如我们此时插入的数据是32-112-82-2-192,此时它们的依次累加的时候步长是相同的,也就是这种方式情况下回造成步长不一样的一种聚集,还是会影响效率(这种影响效率相对于连续的数字会小一些)。使用再哈希法解决这个问题
为了消除线性探测和二次探测中无论步长+1还是平法中存在的问题,还有一种最常用的解决方案:再哈希法
再哈希法
把关键字用另外一个哈希函数,再做一个哈希化,用这次哈希化的结果作为步长,对于指定的关键字,步长在整个探测中是不变的,不过不同的关键字使用了不同的步长
第二次哈希化需要具备以下特点:
和第一个哈希函数不同,否则结果还是原来的位置
不能输出为0,否则将没有步长,每次探测都是原地踏步,算法就进入了死循环
计算机专家已经设计好一种很好的哈希函数:
stepSize = constant - (key - constant)
constant是质数,且小于数组的容量
哈希化的效率
哈希表中执行插入和搜索操作的效率是非常高的
如果没有产生冲突,那么效率会更高
如果发生冲突,存取事件就依赖后来的探测长度
平均探测长度以及平均存取时间,取决于填装因子,随着填装因子变大,探测长度也越来越长
随着填装因子变大,效率下降的情况,在不同开放地址法方案中比链地址法更严重
什么是填装因子?
填装因子表示当前哈希表中已经包含的数据项和整个哈希表长度的比值
填装因子=总数据项/哈希表长度
开放地址的装填因子最大为1,因为它必须寻找到空白的单元才能将元素放入
链地址法的填装因子可以大于1,因为链地址法可以无限的延伸下去,当然后面的效率会变低
优秀的哈希函数
好的哈希函数应该尽可能的让计算的过程编的简单,提高计算的效率
哈希表的主要有点就是它的速度,所以在速度上不能满足就达不到设计的目的,提高速度的一个办法就是让哈希函数中尽量少的乘法和除法,因为他们的性能比较低。
好的哈希函数应该具备哪些优点?
快速的计算:
1、哈希表的优势就在于效率,所以快速获取到对应的hashCode非常重要
2、通过快速的计算来获取到元素对应的ehashCode
均匀的分布:
1、哈希表中,无论是链地址还是地址法,当多个元素映射带同一个位置的时候,都会影响到效率
2、优秀的哈希函数应该尽可能的讲元素映射到不同的位置,让元素在哈希表中均匀的分布
哈希表的长度
哈希表的长度最好使用质数
再哈希法中质数的重要性:假设表的容量不是质数(表长为15,下标值0-14),有一个特定关键字映射到0,步长为5,探测序列是多少呢?0-5-10-0-5-10,一次类推,算法只尝试着三个单元,如果这三个单元都有了数据,那么就会一致循环下去,如果容量为质数(比如13),探测序列就为0-5-10-2-7-12-4-9-1,一直这样下午,不仅不会产生循环,而且可以让数据在哈希表中更加均匀的分布,在链地址法中没有那么重要。
哈希函数的实现
//设计哈希函数 /* * 1、将字符串转换成比较大的数字:hashCode * 2、将大的数字hashCode压缩成数组范围内 * */ function hashFunc(str,size) { //定义hashCode变量 var hashCode = 0 //计算hashCode的值 for (var i = 0; i < str.length; i++) { hashCode = 37 * hashCode + str.charCodeAt(i) //使用37的比较多 } //取余操作 var index = hashCode % size return index } //测试哈希函数 alert(hashFunc('abc',7)) //4 alert(hashFunc('cba',7)) //3 alert(hashFunc('nba',7)) //5 alert(hashFunc('mba',7)) //1
经过测试得到的下标值分布还是挺均匀的
使用链地址法实现哈希表
哈希表的插入和修改操作是同一个函数,如果原来不存在该key,那么就是插入操作,如果已经存在该key,那么就是删除操作
插入和修改方法的实现
思路:
1、根据key获取索引值,目的是将数据插入的对应的位置
2、根据索引值取出bucket桶 如果桶不存在,创建桶并放在该索引的位置
3、判断是新增还是修改原来的值,如果有值就修改值,如果没有就添加
4、新增操作
//封装哈希表类 function HashTable() { //属性 this.storage = [] this.count = 0 //记录当前存放多少个元素 this.limit = 7 //哈希表总长度 //方法 //哈希函数 HashTable.prototype.hashFunc = function (str, size) { //定义hashCode变量 var hashCode = 0 //计算hashCode的值 for (var i = 0; i < str.length; i++) { hashCode = 37 * hashCode + str.charCodeAt(i) //使用37的比较多 } //取余操作 var index = hashCode % size return index } //插入和修改操作 HashTable.prototype.put = function (key, value) { //1、根据key获取对应的index var index = this.hashFunc(key, this.limit) //2、根据index获取bucket var bucket = this.storage[index] //根据索引值取出对应位置的桶 //3、判断bucket是否为空 if (bucket == null) { bucket = [] this.storage[index] = bucket } //4、判断是否是修改数据 for (var i = 0; i < bucket.length; i++) { var tuple = bucket[i] if (tuple[0] == key) { tuple[1] = value return } } //5、添加操作 bucket.push([key,value]) this.count += 1 } }
获取操作方法的实现
思路:
1、根据key获取对应的index
2、根据index获取对应的bucket
3、判断bucket是否为null,如果为null直接返回null
4、线性查找bucket中每一个key是否等于传入key,如果等于,直接返回对应的value
5、遍历完后,依然没有找到,直接返回对应null即可
//获取操作 HashTable.prototype.get = function (key) { //根据key获取对应的index var index = this.hashFunc(key, this.limit) //根据index获取对应的bucket var bucket = this.storage[index] //判断bucket是否为null if (bucket == null) return null //进行线性查找 for (var i = 0; i < bucket.length; i++) { var tuple = bucket[i] if (tuple[0] == key) return tuple[1] } //没有找到返回null return null }
删除操作方法的实现
思路:
1、根据key获取对应的index
2、根据index获取对应的bucket
3、判断bucket是否为存在,如果不存在直接返回null
4、线性查找bucket,寻找对应的数据删除即可
5、遍历完后,依然没有找到,直接返回对应null即可
HashTable.prototype.remove = function (key) { //根据key获取对应的index var index = this.hashFunc(key, this.limit) //根据index获取对应的bucket var bucket = this.storage[index] //判断bucket是否为null if (bucket == null) return null //进行线性查找并且删除 for (var i = 0; i < bucket.length; i++) { var tuple = bucket[i] if (tuple[0] == key) { bucket.splice(i,1) this.count-- return tuple[1] } } //没有找到返回null return null }
判断哈希表是否为空
HashTable.prototype.isEmpty = function () { return this.count == 0 }
哈希表的长度
HashTable.prototype.size = function () { return this.count }
哈希表的扩容
为什么需要扩容?
目前,我们是将所有的数据项放在长度为7的数组中,因为使用的是链地址法,loadFactor(填装因子,count和limit的比值)可以大于1,所以这个哈希表可以无限制的插入新数据,但是随着数据量的增多,每一个index对应的bucket会越来越长,也就会造成效率的降低,所以在合适的情况下对数组进行扩容
主要是在增加数据额和删除数据的时候进行判断,是否需要扩容,缩容
//封装哈希表类 function HashTable() { //属性 this.storage = [] this.count = 0 //记录当前存放多少个元素 this.limit = 7 //哈希表总长度 //方法 //哈希函数 HashTable.prototype.hashFunc = function (str, size) { //定义hashCode变量 var hashCode = 0 //计算hashCode的值 for (var i = 0; i < str.length; i++) { hashCode = 37 * hashCode + str.charCodeAt(i) //使用37的比较多 } //取余操作 var index = hashCode % size return index } //插入和修改操作 HashTable.prototype.put = function (key, value) { //1、根据key获取对应的index var index = this.hashFunc(key, this.limit) //2、根据index获取bucket var bucket = this.storage[index] //根据索引值取出对应位置的桶 //3、判断bucket是否为空 if (bucket == null) { bucket = [] this.storage[index] = bucket } //4、判断是否是修改数据 for (var i = 0; i < bucket.length; i++) { var tuple = bucket[i] if (tuple[0] == key) { tuple[1] = value return } } //5、添加操作 bucket.push([key, value]) this.count += 1 //判断是否需要进行扩容操作 if (this.count > this.limit * 0.75) { this.reSize(this.limit * 2) } } HashTable.prototype.remove = function (key) { //根据key获取对应的index var index = this.hashFunc(key, this.limit) //根据index获取对应的bucket var bucket = this.storage[index] //判断bucket是否为null if (bucket == null) return null //进行线性查找并且删除 for (var i = 0; i < bucket.length; i++) { var tuple = bucket[i] if (tuple[0] == key) { bucket.splice(i, 1) this.count-- return tuple[1] //判断是否缩小容量 if (this.limit > 7 && this.count < this.limit * 0.25) { this.reSize(Math.floor(this.limit / 2)) } } } //没有找到返回null return null } //扩容 HashTable.prototype.reSize = function (newLimit) { //1、保存旧的数组内容 var oldStorage = this.storage //2、重置所有属性 this.storage = [] this.count = 0 this.limit = newLimit //3、遍历oldStorage中所有的bucket for (var i = 0; i < oldStorage.length; i++) { //取出对应的bucket var bucket = oldStorage[i] if (bucket == null) { continue } //bucket中有数据 for (var j = 0; j < bucket.length; j++) { var tuple = bucket[j] this.put(tuple[0], tuple[1]) } } } }
容量质数
判断质数的方法
//判断质数 function fun(num) { for (var i = 2; i < num; i++) { if (num % i == 0) return false } return true } console.log(fun(5)) //true
更高效的判断质数的方法
对于一个数,可以进行因数分解,分解时得到的两个数一定是一个小于等于sqrt(n),一个大于sqrt(n)
所以只需要判断开平根的位置就可以了
function fun2(num) { var sqnum = parseInt(Math.sqrt(num)) for(var i=2;i<sqnum;i++){ if(num%i==0) return false } return true } console.log(fun2(5))
使哈希表的容量恒为质数
//封装哈希表类 function HashTable() { //属性 this.storage = [] this.count = 0 //记录当前存放多少个元素 this.limit = 7 //哈希表总长度 //方法 //哈希函数 HashTable.prototype.hashFunc = function (str, size) { //定义hashCode变量 var hashCode = 0 //计算hashCode的值 for (var i = 0; i < str.length; i++) { hashCode = 37 * hashCode + str.charCodeAt(i) //使用37的比较多 } //取余操作 var index = hashCode % size return index } //插入和修改操作 HashTable.prototype.put = function (key, value) { //1、根据key获取对应的index var index = this.hashFunc(key, this.limit) //2、根据index获取bucket var bucket = this.storage[index] //根据索引值取出对应位置的桶 //3、判断bucket是否为空 if (bucket == null) { bucket = [] this.storage[index] = bucket } //4、判断是否是修改数据 for (var i = 0; i < bucket.length; i++) { var tuple = bucket[i] if (tuple[0] == key) { tuple[1] = value return } } //5、添加操作 bucket.push([key, value]) this.count += 1 //判断是否需要进行扩容操作 if (this.count > this.limit * 0.75) { var newSize = this.size * 2 var newPrime = this.getPrime(newSize) this.reSize(newPrime) } } HashTable.prototype.remove = function (key) { //根据key获取对应的index var index = this.hashFunc(key, this.limit) //根据index获取对应的bucket var bucket = this.storage[index] //判断bucket是否为null if (bucket == null) return null //进行线性查找并且删除 for (var i = 0; i < bucket.length; i++) { var tuple = bucket[i] if (tuple[0] == key) { bucket.splice(i, 1) this.count-- return tuple[1] //判断是否缩小容量 if (this.limit > 7 && this.count < this.limit * 0.25) { var newSize = Math.floor(this.limit / 2) var newPrime = this.getPrime(newSize) this.reSize(newPrime) } } } //没有找到返回null return null } //判断是不是质数 HashTable.prototype.isPrime = function (num) { var temp = parseInt(Math.sqrt(num)) for (var i = 2; i < temp; i++) { if (num % i == 0) return false } return true } //获取质数 HashTable.prototype.getPrime = function (num) { while(!this.isPrime(num)){ num++ } return num } }



