机器学习泛化能力的评价指标

目录

• 一、回归模型评估
  • 1.均方误差
  • 2.绝对误差
  • 3.r2
  • 4.可解释方差
• 二、分类模型评估
  • 1.错误率与准确率
  • 2.精确率、召回率、F1
  • 3. ROC 与 AUC

对机器学习泛化能力的评估，不仅需要可行的估计方法，还需要衡量模型泛化能力的标准，这就是性能度量（$performance\ measure$）。

模型的 “好坏” 不仅取决于算法和数据，还取决于任务需求。

一、回归模型评估

指标	描述	sklearn函数
$Mean\ Squred\ Error\ (MSE,RMSE)$	均方误差	from sklearn.metrics import mean_squared_error
$Absolute\ Error\ (MAE,RAE)$	绝对误差	from sklearn.metrics import mean_absolute_error, median_absolute_error
$R-Squared$	$R$平方值	from sklearn.metrics import r2_score
$Explained\ Variance\ Score$	可解释方差	from sklearn.metrics import explained_variance_score

1.均方误差

给定样例集 $D=\{(x_1,y_1),(x_2,y_2),...,(x_m,y_m)\}$，$y_i$ 是示例 $x_i$ 的真实标记，$f(x)$ 是预测结果。

回归模型最常用的性能度量是均方误差（$Mean\ Squared\ Error$），数值越小越好。

$$MSE = \frac{1}{m} \sum_{i=1}^{m} (f(x_i) - y_i)^2$$

2.绝对误差

绝对误差（$Mean\ Absolute\ Error$）用来描述预测值与真实值的差值。数值越小越好。

$$MAE = \frac{1}{m} \sum_{i=1}^{m} |f(x_i) - y_i|$$

3.r2

给定样例集 $D=\{(x_1,y_1),(x_2,y_2),...,(x_m,y_m)\}$，$y_i$ 是示例 $x_i$ 的真实标记，$f(x)$ 是预测结果。

值最大为 $1$，越接近 $1$ 越好。

$$\begin{aligned} & \bar{y} = \frac{1}{m} \sum_{i=1}^{m} y_i \\ \\ & R^2 = 1 - \frac{\sum_{i=1}^{m}(y_i - f(x_i))^2} {\sum_{i=1}^{m}(y_i - \bar{y})^2} \end{aligned}$$

4.可解释方差

可解释方差（$Explained\ Variance\ Score$），值最大为 $1$，越接近 $1$ 越好。

$$Explained\ Variance = 1-\frac{Var(y_i- f(x_i))}{Var(y_i)}$$

二、分类模型评估

指标	描述	sklearn函数
$Precision$	精确率、查准率	from sklearn.metrics import precision_score
$Recall$	召回率、查全率	from sklearn.metrics import recall_score
$F1$	$F1$ 值	from sklearn.metrics import f1_score
$Confusion\ Matrix$	混淆矩阵	from sklearn.metrics import confusion_matrix
$ROC$	$ROC$ 曲线	from sklearn.metrics import confusion_matrix
$AUC$	$ROC$ 曲线下的面积	from sklearn.metrics import auc

1.错误率与准确率

分类模型最常用的两种性能度量，既适用二分类，也适用多分类。

错误率：分类错误的样本数占总样本数的比例。

准确率（$Accuracy$）：分类正确的样本数占总样本数的比例。

对样例集 $D$，分类错误率

$$E(f;D) = \frac{1}{m} \sum_{i=1}^{m} I(f(x_i)≠y_i)$$

准确率

$$\begin{aligned} acc(f;D) & = \frac{1}{m} \sum_{i=1}^{m} I(f(x_i)=y_i) \\ & = 1-E(f;D) \end{aligned}$$

准确率在很多项目场景不适用，原因是样本不均衡时，准确率会失效。

例：一个总样本中，正样本占90%，负样本占10%，样本严重不平衡。这时候如果将全部正样本预测为正样本，即可达到90%的准确率。

2.精确率、召回率、F1

对于二分类问题，根据真实情况与预测结果划分为：

真正例（$true\ positive,\ TP$）、假正例（$false\ positive,\ FP$）、真反例（$true\ negative,\ TN$）、假反例（$false\ negative,\ FN$）。$TP+FP+TN+FN=样本总数$。

分类结果的 “混淆矩阵”：

真实情况	预测结果	预测结果
	正例	反例
正例	$TP$（真正例）	$FN$（假反例）
反例	$FP$（假正例）	$TN$ （真反例）

查准率，也称精确率（$Precision$）：被预测为正的正样本数 / 被预测为正的样本总数（预测的准不准，看预测列）

$$P = \frac{TP}{TP+FP}$$

查全率，也称召回率（$Recall$）：被预测为正的正样本数 / 正样本实际数（预测的全不全，看实际行）

$$R = \frac{TP}{TP+FN}$$

查准率和查全率是相矛盾的，查准率高时，查全率偏低；查全率高时，查准率偏低。

以查准率为纵轴，查全率为横轴作图，得到查准率-查全率曲线，简称 “$P-R$ 曲线”，显示该曲线的图称为 "$P-R$ 图"。

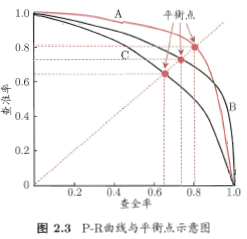
平衡点（$Break-Event\ Point,\ BEP$）：“查准率=查全率” 时的取值。$C$ 的 $BEP$ 是 $0.64$。

$BEP$ 还是过于简化，更常用的是 $F1$ 度量：查准率和查全率的调和均值。

$$\begin{aligned} &\frac{2}{F1} = \frac{1}{P} + \frac{1}{R} \\ \\ & F_1 = \frac{2TP}{2TP+FP+FN} \end{aligned}$$

因为查准率和查全率是相矛盾的，很难同时提高，所以用 $F1$ 综合二者。$F1$ 更接近于两个数较小的那个，当查全率和查准率接近时 $F1$ 值最大。很多推荐系统用 $F1$ 作为评测指标。

3. ROC 与 AUC

$ROC$ 全称 “受试者工作特征”（$Receiver\ Operating\ Characteristic$）。

绘制 $ROC$ 曲线，需要理解三个概念：$TPR$，$FPR$，截断点。

截断点：分类过程中以某个“截断点”将预测样本分为两类，一部分正类，一部分负类。

比如：一个样本预测为正类的概率为0.4，取截断点为0.5，则这个样本为负类，取截断点为0.3，这个样本为正类。

真正率（$True\ Position\ Rate,TPR$）：$TPR = \frac{TP}{TP+FN}$，即 被预测为正的正样本数 / 正样本实际数。等价于召回率。

假正率（$False\ Positive\ Rate,FPR$）：$FPR = \frac{FP}{FP+TN}$，即 被预测为正的负样本数 / 负样本实际数。

假负率（$False\ Negative\ Rate,FNP$）：$FNR = \frac{FN}{TP+FN}$，即 被预测为负的正样本数 / 正样本实际数。

真负率（$True\ Negative\ Rate,TNP$）：$TNR = \frac{TN}{TN+FP}$，即 被预测为负的负样本数 / 负样本实际数。

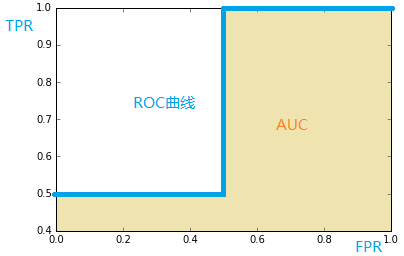
$ROC$ 曲线：纵轴是 "真正率（$TPR$）"，横轴是 “假正率（$FPR$）”。截断点取值不同，$TPR$、$FPR$ 计算结果也不同，将截断点不同取值下对应的 $TPR$、$FPR$ 结果画在二维坐标系中得到的曲线，就是 $ROC$ 曲线。

$ROC$ 曲线中，$FPR$ 越低 $TPR$ 越高（即曲线越陡峭），模型越好。$ROC$ 曲线无视样本不均衡。

$AUC$ 曲线：$ROC$ 曲线下的面积。全称“曲线下的面积”（$Area\ Under\ The\ Curve$）。

import numpy as np
from sklearn import metrics

y = np.array([1, 1, 2, 2])		# 样本的真实分类
scores = np.array([0.1, 0.4, 0.35, 0.8])    # y 是正类的概率估计[0.1, 0.4, 0.35, 0.8]
fpr, tpr, thresholds = metrics.roc_curve(y, scores, pos_label=2)     # FPR、TPR、截断点

print(fpr)
print(tpr)
print(thresholds)

[0.  0.  0.5 0.5 1. ]
[0.  0.5 0.5 1.  1. ]
[1.8  0.8  0.4  0.35 0.1 ]

pos_label：正类的标签。如果y不在 $\{-1,1\}$ 或 $\{0,1\}$ 时，pos_label设置为 $2$，否则引发错误。

thresholds[0]表示没有实例被预测并且任意设置为max(scores) + 1

分析：

y表示类别 $\{1,2\}$。假设y中 $1$ 表示反例，$2$ 表示正例。则y重写为：

y_true = [0, 0, 1, 1]

样本	预测是 $1$ 的概率	y_true
y[0]	$0.1$	$0$
y[1]	$0.4$	$0$
y[2]	$0.35$	$1$
y[3]	$0.8$	$1$

① 截断点为 $0.1$

当 $scores \geqslant 0.1$，预测类别为 $1$。此时，因为 $4$ 个样本都 $\geqslant 0.1$，所以y_pred = [1, 1, 1, 1]。

scores = [0.1, 0.4, 0.35, 0.8]
y_true = [0, 0, 1, 1]
y_pred = [1, 1, 1, 1]

真实值	预测值	预测值
	正例	反例
正例	$TP=2$	$FN=0$
反例	$FP=2$	$TN=0$

$TPR = \frac{TP}{TP+FN} = 1$

$FPR = \frac{FP}{TN+FP} = 1$

② 截断点为 $0.4$

当 $scores \geqslant 0.4$，预测类别为 $1$，所以y_pred = [0, 1, 0, 1]

scores = [0.1, 0.4, 0.35, 0.8]
y_true = [0, 0, 1, 1]
y_pred = [0, 1, 0, 1]

真实值	预测值	预测值
	正例	反例
正例	$TP=1$	$FN=1$
反例	$FP=1$	$TN=1$

$TPR = \frac{TP}{TP+FN} = 0.5$

$FPR = \frac{FP}{TN+FP} = 0.5$

③ 截断点为 $0.35$

当 $scores \geqslant 0.35$，预测类别为 $1$，所以y_pred = [0, 1, 1, 1]

scores = [0.1, 0.4, 0.35, 0.8]
y_true = [0, 0, 1, 1]
y_pred = [0, 1, 1, 1]

真实值	预测值	预测值
	正例	反例
正例	$TP=2$	$FN=0$
反例	$FP=1$	$TN=1$

$TPR = \frac{TP}{TP+FN} = 1$

$FPR = \frac{FP}{TN+FP} = 0.5$

④ 截断点为 $0.8$

当 $scores \geqslant 0.8$，预测类别为 $1$，所以y_pred = [0, 0, 0, 1]

scores = [0.1, 0.4, 0.35, 0.8]
y_true = [0, 0, 1, 1]
y_pred = [0, 0, 0, 1]

真实值	预测值	预测值
	正例	反例
正例	$TP=1$	$FN=1$
反例	$FP=0$	$TN=2$

$TPR = \frac{TP}{TP+FN} = 0.5$

$FPR = \frac{FP}{TN+FP} = 0$

来自：https://www.biaodianfu.com/regression-metrics.html