异常值判断

异常值也称离群点，异常值分析也称离群点分析。

 

1. 简单统计量分析

最常用的是最大值和最小值，超出合理范围为异常。如客户年龄为199岁，该值为异常。

 

2. 3σ原则

(1)、如果数据服从正态分布，在3σ原则下，异常值被定义为与平均值偏差超过3倍标准差的值。

在正态分布情况下，距离平均值3α之外的值出现的概率为 P(|x-μ|>3σ) ≤ 0.0027，属于极个别的小概率事件。

(2)、如果数据不服从正态分布，也可以用远离平均值的多少倍标准差来描述。

 

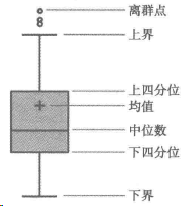
3. 箱型图判断

箱型图提供识别异常值的一个标准：异常值被定义为小于 Q_L-1.5IQR 或 大于Q_u+1.5IQR的值。

Q_L为下四分位数，表示全部观察值中有四分之一的数据比它小；

Q_u为上四分位数，表示全部观察值中有四分之一的数据比它大；

IQR为四分位数间距，是上四分位与下四分位之差，其中包含了观察值的一半。

 

 

 

 

 

 

 

 

import pandas as pd
catering_sale = './catering_sale.xls'       # 餐饮数据
data = pd.read_excel(catering_sale, index_col = u'日期')   # 读取数据，指定“日期”列为索引列 


import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']     # 用来显示中文标签
plt.rcParams['axes.unicode_minus'] = False       # 用来正常显示负号



plt.figure()
p = data.boxplot()                   # 画箱线图，直接使用DataFrame方法
x = p['fliers'][0].get_xdata()       # 'flies'为异常值的标签
y = p['fliers'][0].get_ydata()
y.sort()


# 用annotate添加注释
# 其中有些相近的点，注释会出现重叠，难以看清，需要一些技巧来控制
# 以下参数都是经过调试的，需要具体问题具体调试
for i in range(len(x)):
    if i>0:
        plt.annotate(y[i], xy = (x[i], y[i]), xytext=(x[i]+0.05 - 0.8/(y[i]-y[i-1]),y[i]))
    else:
        plt.annotate(y[i], xy = (x[i], y[i]), xytext=(x[i]+0.08,y[i]))
plt.show()

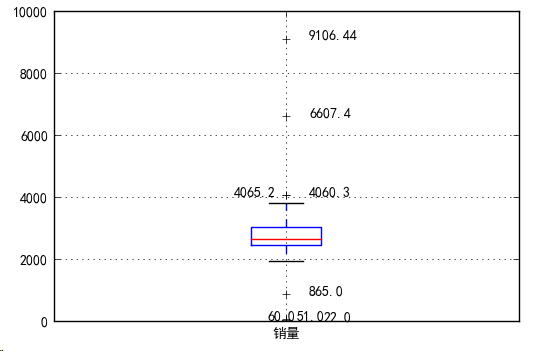
箱型图中超过上下界的8个销售额数据可能为异常值。结合业务把865、4060.3、4065.2归为正常值，将22、51、60、6607.4、9106.44归为异常值。最后确定过滤规则为：400以下5000以上为异常值。

 

4. Z-Score判断

这里使用Z标准化的阈值作为判断标准，当标准化后的得分超过阈值为异常。

import pandas as pd

df = pd.DataFrame({'col1': [1, 120, 3, 5, 2, 12, 13],
                   'col2' : [12, 17, 31, 53, 22, 32, 43]})
print(df)

# 通过Z-Score方法判断异常值
df_zscore = df.copy()   # 通过df.copy()复制一个原始数据框的副本用来存储Z-Score标准化后的得分
for col in df.columns:
    z_score = (df[col] - df[col].mean()) / df[col].std()
    df_zscore[col] = z_score.abs() > 2.2    # 判断Z-score得分是否大于2.2，如果是则是True,否则为False
print(df_zscore)

       　　

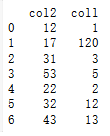
阀值的设定是确定异常与否的关键，通常当阀值大于2时，已经是相对异常的表现值。

 

总结：  如何判断异常值

除了上述4中简单方法外，还可以采用常见的数学模型进行判断：

基于概率分布的模型（例如正态分布的标准差范围）、

基于聚类的方法（例如KMeans）、

基于密度的方法（例如LOF）、

基于分类的方法（例如KNN）、

基于统计的方法（例如分位数法）等。