PCA 主成分分析
主成分分析(\(principal\ component\ analysis, PCA\))是无监督学习方法。该方法将原来由线性相关变量表示的数据,通过正交变换,变成少数由线性无关的新变量表示的数据,线性无关的变量称为主成分。
\(PCA\) 的变量个数通常小于原始变量的个数,属于降维方法。
一、总体主成分分析
1、基本思想
1.1、步骤
① 数据规范化处理(使数据在每一变量的平均值为0,方差为1)。
② 正交变换,即乘以正交矩阵,得到新变量(新坐标轴),新变量线性无关。(新变量是所有正交变换中,变量的方差和最大的)。
1.2、PCA 直观解释
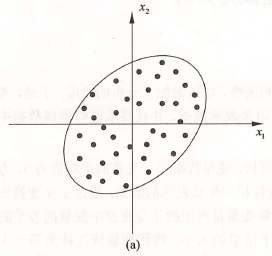
数据规范化处理后分布在原点附近(如图 \(a\))。
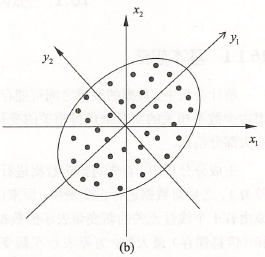
对原坐标系中的数据进行主成分分析等价于进行坐标系旋转变换(如图 \(b\))。
将数据投影到新坐标系的坐标轴上,\(PCA\) 选择方差和最大的方向为新坐标系的第一坐标轴(第一主成分),依次类推。
例如:
图 \(a\) 中,数据由变量 \(x_1\)、\(x_2\)表示,每个点表示一个样本。很明显变量 \(x_1\)、\(x_2\) 是线性相关的(即已知变量 \(x_1\),对变量 \(x_2\) 预测不是完全随机的)。
图 \(b\) 中,通过正交变换,数据由变量 \(y_1\)、\(y_2\) 表示,\(PCA\) 选择方差和最大的方向为第一坐标轴,即 \(y_1\) 轴;之后选择与第一坐标轴正交,且方差和次之的方向为第二坐标轴,即 \(y_2\) 轴。此时变量 \(y_1\)、\(y_2\) 是线性无关的。(即已知变量 \(y_1\),对变量 \(y_2\) 预测是完全随机的)。
主成分分析只取第一主成分时将二维数据压缩成一维。
1.3、方差最大的解释
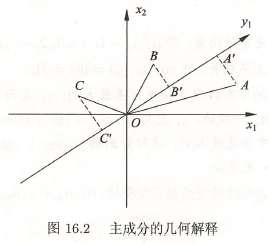
如图 \(16.2\),变量 \(x_1\)、\(x_2\),样本点 \(A\)、\(B\)、\(C\),对坐标系旋转变换,得到新的坐标轴 \(y_1\),表示新的变量 \(y_1\)。
样本点 \(A\)、\(B\)、\(C\) 在 \(y_1\) 轴的投影 \(A'\)、\(B'\)、\(C'\),样本在变量 \(y_1\) 上的方差和 \(OA'^2+OB'^2+OC'^2\)。主成分分析旨在选取正交变换中方差和最大的变量,作为第一主成分。
注意 \(OA^2+OB^2+OC^2\) 不变, \(OA'^2+OB'^2+OC'^2\) 最大等价于 \(AA'^2+BB'^2+CC'^2\) 最小。所以样本点在新变量上的方差和最大等价于样本点在新坐标轴上的投影尽可能的分开或到新坐标轴的距离足够近。
在数据总体上进行主成分分析,是总体主成分分析;
在有限样本上进行主成分分析,是样本主成分分析。
2、定义和导出
假设 \(\pmb{x}=(x_1,x_2,...,x_m)^T\) 是 \(m\) 维随机变量,其均值向量是 \(\pmb{\mu}\)( 均值向量,随机向量的数学期望。):
协方差矩阵 \(\Sigma\)
考虑由 \(m\) 维随机变量 \(\pmb{x}\) 到 \(m\) 维随机变量 \(\pmb{y}=(y_1,y_2,...,y_m)^T\) 的线性变换
其中 \(\alpha_i^T=(\alpha_{1i},\alpha_{2i},...,\alpha_{mi}),\ \ i=1,2,..,m\)。
由随机变量的性质可知:
例 \(1\):\(\pmb{x}=\begin{bmatrix} 4 & 5 & 3 & 4\\ 6 & 2 & 1 & 3 \end{bmatrix}\),求 \(\Sigma\)。
解:
import numpy as np
x = np.array([[4, 5, 3, 4],
[6, 2, 1, 3]])
print(np.cov(x)) # 求协方差矩阵
[[0.66666667 0.33333333]
[0.33333333 4.66666667]]
2.1、总体主成分
给定式 \((1)\) 的线性变换满足下列条件,称为总体主成分:
(1)系数向量 \(\alpha_i^T\) 是单位向量,即 \(\alpha_i^T\alpha_i=1\) ,\(\ \ i=1,2,...,m\);
(2)变量 \(y_i\) 与 \(y_j\) 互不相关,即 \(cov(y_i, y_j)=0(i≠j)\);
(3)变量 \(y_1\) 是 \(\pmb{x}\) 的所有线性变换中方差最大的;\(y_2\) 是与 \(y_1\) 不相关的 \(\pmb{x}\) 所有线性变化中方差最大的;一般,\(y_i\) 是与 \(y_1,y_2,...,y_{i-1}\ \ (i=1,2,...,m)\)都不相关的 \(\pmb{x}\) 的所有线性变换中方差最大的;这时分别称 \(y_1,y_2,...,y_m\) 为 \(\pmb{x}\) 的第一主成分、第二主成分、...、第 \(m\) 主成分。
条件 \((1)\) 表明线性变换是正交变换,\(\alpha_1, \alpha_2,...,\alpha_m\) 是其一组标准正交基,
条件 \((2)\)\((3)\) 给出求主成分的方法:
第一步,在 \(\pmb{x}\) 的所有线性变换
中,在 \(\alpha_1^T\alpha_1=1\) 条件下,求方差最大的,得到 \(\pmb{x}\) 的第一主成分;
第二步,在 \(\alpha_1^T\pmb{x}\) 不相关的 \(\pmb{x}\) 的所有线性变换
中,在 \(\alpha_2^T\alpha_2=1\) 条件下,求方差最大的,得到 \(\pmb{x}\) 的第二主成分;
第 \(k\) 步,在与 \(\alpha_1^T\pmb{x},\alpha_2^T\pmb{x},...,\alpha_{k-1}^T\pmb{x}\) 不相关的 \(\pmb{x}\) 的所有线性变换
中,在 \(\alpha_k^T\alpha_k=1\) 条件下,求方差最大的,得到 \(\pmb{x}\) 的第 \(k\) 主成分;
如此继续下去,得到 \(\pmb{x}\) 的第 \(m\) 主成分。
3、主要性质
定理: \(\pmb{x}\) 是 \(m\) 维随机变量,\(\Sigma\) 是 \(\pmb{x}\) 的协方差矩阵(即特征向量),\(\Sigma\) 的特征值是 \(\lambda_1\geq\lambda_2\geq...\geq\lambda_m\geq0\),特征值对应的单位特征向量是 \(\alpha_1,\alpha_2,...,\alpha_m\),则 \(\pmb{x}\) 的第 \(k\) 主成分是
\(\pmb{x}\) 的第 \(k\) 主成分的方差是协方差矩阵 \(\Sigma\) 的第 \(k\) 个特征值。
性质:
① 主成分 \(\pmb{y}\) 的协方差矩阵是对角矩阵
其中 \(\lambda_k\) 是 \(\Sigma\) 的第 \(k\) 个特征值,\(\alpha_k\) 是对应的单位特征向量,\(k=1,2,...,m\)。
② 主成分 \(\pmb{y}\) 的方差之和是等于随机变量 \(\pmb{x}\) 的方差之和
其中 \(\sigma_{ii}\) 是 \(x_i\) 的方差,即协方差矩阵 \(\Sigma\) 的对角线元素。
③ 主成分 \(y_k\) 与变量 \(x_i\) 的相关系数 \(\rho(y_k,x_i)\) 称为因子负荷量,表示第 \(k\) 个主成分 \(y_k\) 与变量 \(x_i\) 的相关关系,即 \(y_k\) 对 \(x_i\) 的贡献率。
二、样本主成分分析
样本主成分分析是基于样本协方差矩阵的主成分分析。
给定样本矩阵
其中 \(\pmb{x}_j=(x_{ij},x_{2j},\cdots,x_{mj})^T\) 是 \(\pmb{x}\) 的第 \(j\) 个独立观测样本,\(j=1,2,...,n\)。
\(X\) 的样本协方差矩阵
其中 \(\bar{x}_i=\frac{1}{n}\sum_{k=1}^{n}x_{ik}\)。
给定样本数据矩阵 \(X\),考虑向量 \(\pmb{x}\) 到 \(\pmb{y}\) 的线性变换
这里
如果该线性变换满足下列条件,称为样本主成分。
样本第一主成分 \(y_1=a_1^T\pmb{x}\) 是在 \(a_1^Ta_1=1\) 条件下,使得 \(a_1^T\pmb{x}_j\ \ (j=1,2,...,n)\) 的样本方差 \(a_1^TSa_1\) 最大的 \(\pmb{x}\) 的线性变换;
样本第二主成分 \(y_2=a_2^T\pmb{x}\) 是在 \(a_2^Ta_2=1\) 和 \(a_2^Tx_j\) 与 \(a_1^Tx_j\ \ (j=1,2,...,n)\) 的样本协方差 \(a_1^TSa_2=0\) 条件下,使得 \(a_2^T\pmb{x}_j\ \ (j=1,2,...,n)\) 的样本协方差 \(a_2^TSa_2\) 最大的 \(x\) 的线性变换;
样本第 \(i\) 主成分 \(y_i=a_i^Tx\) 是在 \(a_i^Ta_i=1\) 和 \(a_i^T\pmb{x_j}\) 与 \(a_k^T\pmb{x}_j\ \ (k<i,\ j=1,2,...,n)\) 的样本协方差 \(a_k^TSa_i=0\) 条件下,使得 \(a_i^T\pmb{x}_j\ (j=1,2,...,n)\) 的样本方差 \(a_i^TSa_i\) 最大的 \(\pmb{x}\) 的线性变换。
三、PCA 两种实现方法
\(PCA\) 主要有两种,通过相关矩阵的特征值分解或样本矩阵的奇异值分解进行。(相关矩阵指将样本矩阵标准化后再求其相关系数矩阵。)
① 相关矩阵的特征值分解。
针对 \(m\times n\) 样本矩阵 \(X\),求相关矩阵
求相关矩阵的 \(k\) 个特征值和特征向量,构造正交矩阵
\(V\) 的每一列对应一个主成分,得到 \(k\times n\) 样本主成分矩阵
② 样本矩阵的奇异值分解。
针对 \(m\times n\) 样本矩阵 \(X\)
对矩阵 \(X'\) 进行截断奇异值分解,保留 \(k\) 个奇异值、奇异向量,得到
\(V\) 的每一列对应一个主成分,得到 \(k\times n\) 样本主成分矩阵 \(Y\)
例 \(2\): \(n\) 个学生参加 \(4\) 门考试,将考试成绩看作随机变量的取值,进行标准化处理,得到矩阵 \(R\),
| 课程 | 语文 | 外语 | 数学 | 物理 |
|---|---|---|---|---|
| 语文 | 1 | 0.44 | 0.29 | 0.33 |
| 外语 | 0.44 | 1 | 0.35 | 0.32 |
| 数学 | 0.29 | 0.35 | 1 | 0.60 |
| 物理 | 0.33 | 0.32 | 0.60 | 1 |
对数据进行主成分分析。
解: \(x_1,x_2,x_3,x_4\) 表示语、外、数、物。
① 求矩阵的特征值,按大小排序,
import numpy as np
a = np.array([[1, 0.44, 0.29, 0.33],
[0.44, 1, 0.35, 0.32],
[0.29, 0.35, 1, 0.6],
[0.33, 0.32, 0.6, 1]])
w, v = np.linalg.eig(a) # 求矩阵的特征值和特征向量
print(w)
[2.17016506 0.87100546 0.56617908 0.3926504 ]
这些特征值是主成分的方差贡献率。累积方差大于 \(75\%\),只需前两个主成分,即 \(k=2\),
② 求 \(\lambda_1\),\(\lambda_2\) 的特征向量;方差贡献率,
| 项目 | \(x_1\) | \(x_2\) | \(x_3\) | \(x_4\) | |
|---|---|---|---|---|---|
| \(y_1\) | 0.460 | 0.476 | 0.523 | 0.537 | \(\frac{2.17}{2.17+0.87+0.57+0.39}=0.543\) |
| \(y_2\) | 0.574 | 0.486 | -0.476 | -0.456 | \(\frac{0.87}{2.17+0.87+0.57+0.39}=0.218\) |
print(v) # Python处理自带的误差
[[-0.45990769 -0.56790937 -0.6665586 -0.14718523]
[-0.4763124 -0.49090704 0.71535364 0.14284941]
[-0.52874972 0.47557056 0.11286206 -0.69391536]
[-0.53106981 0.45860862 -0.17672284 0.69022607]]
按照式 \((5)\) 得第一、第二主成分:
③ 求主成分的因子负荷量,贡献率,
| 项目 | \(x_1\) | \(x_2\) | \(x_3\) | \(x_4\) |
|---|---|---|---|---|
| \(y_1\) | 0.678 | 0.701 | 0.770 | 0.791 |
| \(y_2\) | 0.536 | 0.453 | -0.444 | -0425 |
| \(y_1\)、\(y_2\) 对 \(x_1\) 的贡献率 | 0.747 | 0.679 | 0.790 | 0.806 |
规范化随机变量 \(x_i^*\) 与主成分 \(y_i^*\) 的相关系数(因子负荷量)为
其中 \(e_k^*=(e_{1k}^*,e_{2k}^*,...,e_{mk}^*)^T\) 为矩阵对应特征值 \(\lambda_k^*\) 的单位特征向量。
第一、第二主成分对变量 \(x_i\) 的贡献率,
\(k\) 个主成分 \(y_1,y_2,...,y_k\) 对原有变量 \(x_i\) 的贡献率定义为 \(x_i\) 与 \((y_1,y_2,...,y_k)\) 的相关系数的平方,记作 \(v_i\)
计算公式:
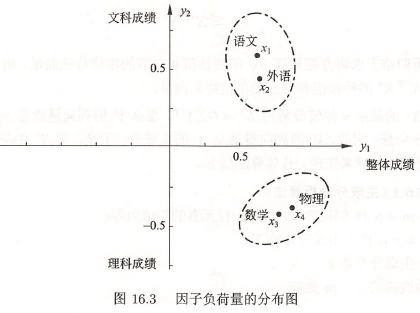
从上表可以看出,
第一主成分 \(y_1\) 对应的因子负荷量 \(\rho(y_1,x_i),\ i=1,2,3,4\), 均为正数,表明各门成绩提高都使 \(y_1\) 提高,也就是说,第一主成分 \(y_1\) 反映学生的整体成绩。还可以看出,因子负荷量的数值相近,且 \(\rho(y_1,x_4)\) 的值最大,这表明物理成绩在整体成绩中占最重要位置。
第二主成分 \(y_2\) 对应的因子负荷量 \(\rho(y_2,x_i),\ i=1,2,3,4\),有正有负,正的是语文、外语,负的是数学、物理 ,表明文科成绩提高可使 \(y_2\) 提高,理科成绩提高可使 \(y_2\) 降低, 也就是说,第二主成分 \(y_2\) 反映文科成绩与理科成绩的关系。
下图是因子负荷量分布图,将原变量 \(x_1,x_2,x_3,x_4\)(语文、外语、数学、物理)和主成分 \(y_1,y_2\)(整体成绩、文科对理科成绩)的因子负荷量在平面坐标系中表示。可以看出变量之间的关系,\(4\) 个原变量聚成了两类:因子负荷量相近的语文、外语为一类,数学、物理为一类,前者反映文科成绩,后者反映理科成绩。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号