SMOTE 过采样算法
1. 算法概要
设训练集的一个少数类样本数为 \(T\)，应用过采样方法生成 \(NT\) 个样本。
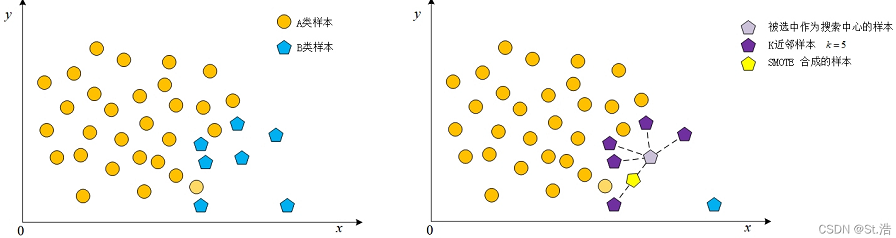
① 从样本数为 \(T\) 的样本中选择一个样本，搜索它的 \(k\) 近邻。
② 从 \(k\) 近邻样本中随机选择一个样本，将这两个样本连接成一条直线，新合成的样本就在这条直线上，重复 \(N\) 次。
③ 总共 \(T\) 个样本，重复步骤② \(T\) 次。
2. 算法步骤
过采样算法 \(SMOTE\) ，概括来说是基于单线性“插值”来合成新的样本。
设训练集的一个少数类样本数为 \(T\)，那么 \(SMOTE\) 算法将为这个少数类合成 \(NT\) 个新样本。这里要求 \(N\) 必须为正整数，如果 \(N<1\)，那么算法将“认为”少数类的样本数 \(T=NT\)，强制 \(N=1\)。
考虑少数类的一个样本 \(x_i\)，\(i \in \{1,2,...,T\}\)：
① 首先从该少数类的全部 \(T\) 个样本中找到样本 \(x_i\) 的 \(k\) 个近邻（例如欧式距离），记为 \(x_{i(near)}\)，\(near \in \{1,2,...,k\}\)
② 然后从这 \(k\) 个近邻中随机选择一个样本 \(x_{i(n)}\)，在生成一个 \(0\) 到 \(1\) 之间的随机数 \(\zeta_1\)，从而合成一个新样本 \(x_{i1}\)
③ 将步骤②重复 \(N\) 次，从而合成 \(N\) 个新样本：\(x_{inew}\)，\(new\in1,2,..,N\)。
那么，对全部的 \(T\) 个少数类样本进行上述操作，便可为该少数类合成 \(NT\) 个新样本。
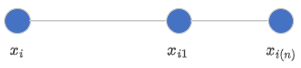
如果样本的特征维数是 \(2\) 维，那么每个样本都可以用二维平面上的一个点来表示。\(SMOTE\) 算法所合成出的一个新样本 \(x_{i1}\) 相当于表示样本 \(x_i\) 的点和表示样本 \(x_{i(n)}\) 的点之间所连线段上的一个点。所以说该算法是基于“插值”来合成新样本。
例 \(1\)：令 \(x_i=x_1\)，\(x_{i(n)} = x_2\)，则 \(x_{i1} = x_1+\zeta_1(x_2-x_1) = x_2 + \zeta_1(x_1-x_2) = \zeta_1x_1 + (1-\zeta_1)x_2\)
