二维卷积层
卷积神经网络(\(convolutional\ neural\ network,CNN\))是含有卷积层的神经网络。本节介绍最常见的二维卷积层。它有高、宽两个维度。
1. 二维卷积运算
虽然卷积层得名于卷积(\(convolution\))运算,但通常在卷积层中使用更加直观的互相关(\(cross-correlation\))运算。
如图 \(5.1\),一个二维输入数组、卷积核或过滤器(\(filter\))通过互相关运算输出一个二维数组。
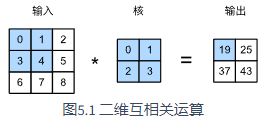
卷积窗口从左往右,从上往下,依次在输入数组上滑动。
示例:corr2d函数,输入数组 \(X\),卷积核 \(K\),输出数组 \(Y\)。
import torch
from torch import nn
def corr2d(X, K):
h, w = K.shape
Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))
for i in range(Y.shape[0]):
for j in range(Y.shape[1]):
Y[i, j] = (X[i: i + h, j: j + w] * K).sum()
return Y
X = torch.tensor([[0, 1, 2], [3, 4, 5], [6, 7, 8]])
K = torch.tensor([[0, 1], [2, 3]])
print(corr2d(X, K))
tensor([[19., 25.],
[37., 43.]])
2. 二维卷积层
卷积层的模型包括卷积核和偏差。在训练模型的时候,通常对卷积核随机初始化,然后不断迭代卷积核和偏差。
示例:基于corr2d函数实现一个自定义二维卷积层。
- 构造函数
__init__里声明weight、bias参数。 forward调用corr2d函数,再加上偏差。
class Conv2D(nn.Module):
def __init__(self, kernel_size):
super(Conv2D, self).__init__()
self.weight = nn.Parameter(torch.randn(kernel_size))
self.bias = nn.Parameter(torch.randn(1))
def forward(self, x):
return corr2d(x, self.weight) + self.bias
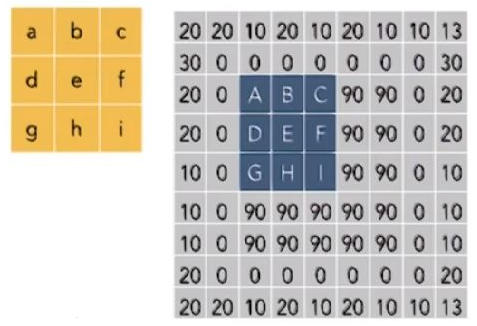
3. 图像中物体边缘检测
图像物体边缘检测,即找到像素变化的位置。
示例:
① 构造 \(6 \times 8\) 的图像(即高和宽分别为 \(6\) 像素和 \(8\) 像素的图像),中间 \(4\) 列为黑(\(0\)),其余为白(\(1\))。
X = torch.ones(6, 8)
X[:, 2:6] = 0
print(X)
tensor([[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.],
[1., 1., 0., 0., 0., 0., 1., 1.]])
② 构造卷积核 \(K = 1 \times 2\)(高和宽分别为 \(1、2\) )。
K = torch.tensor([[1, -1]])
③ 互相关运算。
可以看出,将从白到黑的边缘和从黑到白的边缘分别检测成了 \(1\) 和 \(-1\)。其余部分的输出全是 \(0\)。
Y = corr2d(X, K)
print(Y)
tensor([[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.],
[ 0., 1., 0., 0., 0., -1., 0.]])
因此,卷积层可通过重复使用卷积核有效地表征局部空间。
4. 学习卷积核
使用输入数组 \(X\),输出数组 \(Y\) 学习卷积核 \(K\)。
首先随机初始化卷积核,接下来每次迭代,使用平方误差比较 \(Y\) 和卷积层的输出,计算梯度来更新权重。
示例:
# 构造一个卷积核,形状是(1, 2)的二维卷积层
conv2d = Conv2D(kernel_size=(1, 2))
step = 20 # 迭代次数
lr = 0.01 # 学习率
for i in range(step):
Y_hat = conv2d(X)
l = ((Y_hat - Y) ** 2).sum()
l.backward()
# 梯度下降
conv2d.weight.data -= lr * conv2d.weight.grad
conv2d.bias.data -= lr * conv2d.bias.grad
# 梯度清0
conv2d.weight.grad.fill_(0)
conv2d.bias.grad.fill_(0)
if (i + 1) % 5 == 0:
print('Step %d, loss %.3f' % (i + 1, l.item()))
Step 5, loss 4.442
Step 10, loss 1.222
Step 15, loss 0.339
Step 20, loss 0.094
迭代 \(20\) 次后损失函数很小,此时学习到的卷积核的参数:
print("weight: ", conv2d.weight.data)
print("bias: ", conv2d.bias.data)
weight: tensor([[ 0.9948, -1.0092]])
bias: tensor([0.0080])
可以看到,学到的卷积核的权重与之前定义的卷积核 \(K\) 权重较接近,而偏置接近0。
5. 互相关运算、卷积运算
为了得到卷积运算的输出,只需将卷积核左右反转并上下翻转,再与输入数组做互相关运算。
互相关运算:
卷积运算:
可见,卷积运算和互相关运算类似,但如果它们使用相同的卷积核,对于同一输入,输出往往不同。
那么,为何卷积层能使用互相关运算替代卷积运算?
原因:深度学习中卷积核都是学出来的,卷积层无论使用互相关运算或卷积运算都不影响卷积层的输出。
为了解释这一点,假设卷积层使用互相关运算学出图 \(5.1\) 的核数组。设其他条件不变,使用卷积运算出的核数组即图 \(5.1\) 中的核数组按上下、左右翻转。也就是说,图 \(5.1\) 中的输入与学出的已翻转的核数组再做卷积运算时,依然得到图 \(5.1\) 中的输出。
6. 特征图、感受野
二维卷积层输出的二维数组可以看作是输入在空间维度(宽和高)上某一级的表征,也叫特征图(\(feature\ map\))。
影响元素 \(x\) 的前向计算的所有可能输入区域(可能大于输入的实际尺寸)叫做 \(x\) 的感受野(\(receptive\ field\))。
以图 \(5.1\) 为例,输入中阴影部分的四个元素是输出中阴影部分元素的感受野。
我们将图 \(5.1\) 中形状为 \(2 \times 2\) 的输出记为 \(Y\),并考虑一个更深的卷积神经网络:将\(Y\) 作为输入,与另一个形状为 \(2 \times 2\) 的核数组做互相关运算,输出单个元素 \(z\)。那么,\(z\) 在 \(Y\) 上的感受野包括 \(Y\) 的全部 \(4\) 个元素,而输入上的感受野包括最初全部 \(9\) 个元素。
来自:《动手学深度学习》


 浙公网安备 33010602011771号
浙公网安备 33010602011771号