磁共振成像原理

目录

• 1. 原子核的自旋
• 2. 进动
• 3. 磁共振现象
• 4. 射频脉冲

1. 原子核的自旋

原子有原子核和绕核运动的电子组成。

原子核的自旋：

• 质子数和中子数一个为奇数、一个为偶数；
• 两者都为奇数

这两种情况的原子核就会自旋。

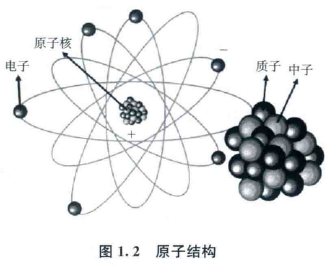
原子核是带正电，绕自旋轴旋转，效应相当于环形电流，周围会产生磁场。

原子核磁矩大小与自旋角动量成正比：

\[\pmb{\mu} = \gamma \pmb{P} \]

其中，\(\pmb{\mu}\) 是磁矩，\(\pmb{p}\) 是角动量矩，\(\gamma\) 是磁旋比（常数）。

2. 进动

进动：自旋核具有自旋角动量和核磁矩，在静磁场作用下，核磁矩像陀螺在地球的引力场中的进动一样运动，称为自旋核的进动，如图 \(1.3\) 所示。

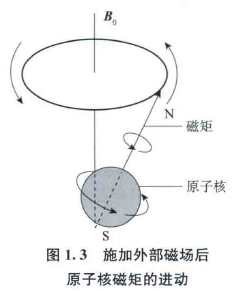
进动角频率 \(w\) 与外磁场 \(B_0\) 的关系：

\[w = \gamma B_0 \]

3. 磁共振现象

在与静磁场 \(B_0\) 垂直的方向上施加频率等于进动频率 \(w\) 的电磁波 \(H_1\) 时，原子核磁矩 \(\mu_N\) 与 \(H_1\) 作用产生力矩 \(\pmb{\tau}\) ：

\[\pmb{\tau} = \pmb{\mu}_N \times \pmb{H}_1 \]

\(\tau\) 可能使质子的自旋改变方向，从电磁波吸收能量，并从 \(M_1 = \frac{1}{2}\) 的能态跃迁至 \(M_1 = -\frac{1}{2}\) 能态，这就是磁共振现象。

吸收的能量等于两个能级的能量差：

\[\triangle E = h \nu = \frac{h \gamma}{2 \pi} B_0 \]

其中，\(\gamma\) 为电磁波辐射的共振频率，\(B_0\) 为外加磁感应强度，\(h\) 为普朗克常量。停止发射辐射脉冲后，部分质子从高能级跃迁到低能级，其相位和能级恢复到激发前的状态，同时向外辐射相同频率的电磁波信号。

磁共振现象简单概括：磁共振现象就是磁场的强度和方向决定了原子核自旋的频率和方向，在磁场中旋转时，原子核吸收频率和进动频率相同的电磁波，是自身能力增加，部分质子能级跃迁。而一旦撤销外部射频照射，跃迁的质子恢复原状，并把多余的能量以电磁波的形式释放出来。

4. 射频脉冲

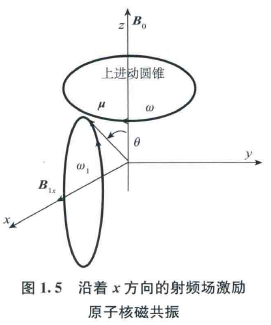
为了获得射频脉冲，通常在如图 \(1.5\) 所示的 \(x\) 轴上的振荡线圈中通交流电，使其产生线偏振磁场 \(B_{1x} = 2B_1 coswt\)。

线偏振磁场分解为两个大小相等、旋转方向相反的圆偏振场。其中，只有旋转方向与核磁矩进动方向一致的圆偏振场能够与其相互作用，激发磁共振信号。

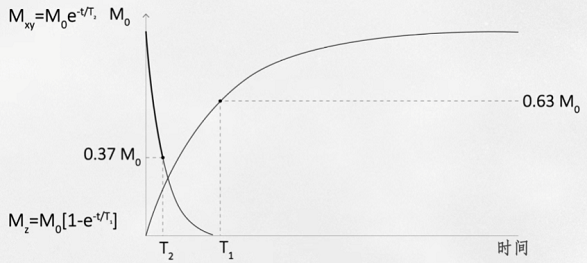
弛豫时间 \(T_1\)：纵向磁分量恢复至稳态值 \(63\%\)​ 的时间。

纵向磁分量随时间变化公式：

\[M_z = M_0 \left[ 1 + (cos \theta - 1) e^{-\frac{1}{T_1}}\right] \]

弛豫时间 \(T_2\)：横向磁分量降低到最大值值 \(37\%\)​ 的时间。

横向磁分量随时间变化公式：

\[\begin{aligned} & M_{xy} = M_0 sin \theta e^{-\frac{t}{T_2}} \\ & M_{xy} = M_0 e^{-i(w_o -\frac{\pi}{2})} \cdot e^{-\frac{t-\tau}{\ T_{2}^{*}}} \end{aligned} \]

其中，\(T^*\) 为特征时间，为质子的本征弛豫（\(T_1、T_2\)）与外部弛豫之和。外部弛豫即磁场不均匀导致的弛豫时间常数。