Xbar-R 控制图
1. Xbar-R控制图
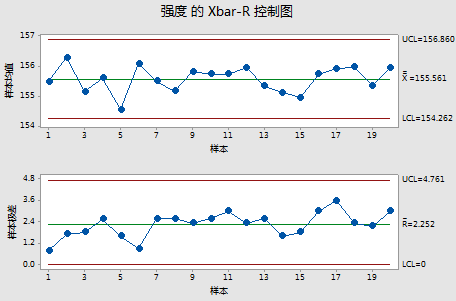
Xbar-R控制图，可以在拥有连续数据且子组大小不超过8的情况下监视过程的均值和变异。
例如：确定新塑料产品的生产过程是否受控。操作员抽样20个小时，每小时抽取5个部件，并评估塑料的强度。
什么情况下使用备择控制图？
对于具有9或更多观测值的子组，使用Xbar-S控制图。
如果子组内存在一致的变异来源，使用I-MR-R/S控制图。
如果没有子组，使用I-MR控制图。
如果数据有缺陷品数或缺陷数，使用属性控制图，如P控制图或U控制图。
2. Xbar-R控制图的数据注意事项
为了确保结果有效，请在收集数据、执行分析和解释结果时考虑以下准则。
1. 数据集应当连续
如果数据中有缺陷品数或缺陷数，使用属性控制图，如P控制图或U控制图。
2. 数据应当采用时间顺序
由于控制图检测会随时间发生的变化，因此数据顺序非常重要。应当按照数据的收集顺序来输入数据。让最旧得数据位于工作表的顶部。
3. 应当按照适当的时间间隔收集数据
按照均匀的时间间隔收集数据，如每小时一次，每班次一次，每天一次。选择一个时间间隔，该时间间隔应当足够短，以便可以在发生过程更改之后立即识别此更改。
4. 数据应当位于合理的子组中
如果子组不合理，则估计的控制限可能太宽。
5. 子组大小应当为8或更少
对于具有9或更多观测值的子组，应当使用Xbar-S控制图。
如果没有子组，请使用 I-MR 控制图。
6. 收集相应的数据量
如果子组大小小于或等于2，至少收集100个观测值。
如果子组大小为3，至少收集80个观测值。
如果子组大小为4或5，至少收集70个观测值。
如果子组大小为6或更大，至少收集60个观测值。
7. 数据不必是正太分布的
大多数控制图在形式上基于正太性假设的，但如果收集子组中的数据，仍可以使用非正太数据得到好的结果。所需的子组大小取决于数据的非正太性。
8. 每个子组内的观测值不应当相互关联
如果每个子组中的连续数据点是相关的，控制限的范围将过窄，而且控制图可能会错误地将一些受控点显示为失控点。
3. 估计Xbar-R控制图的 σ 的方法和公式
σ 是标准差。如果为 σ 输入历史值，则 Minitab 将使用历史值。否则，Minitab使用下列方法从数据估计 σ。
1. Rbar方法
Minitab使用每个子组的极差 ri 计算 Sr ，它是 σ 的无偏估计量：
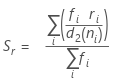
其中
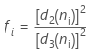
当子组大小固定时，公式简化为以下所示：
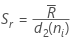
其中，Rbar是子组极差的均值，计算方式为：
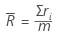
表示法：
| 项 | 说明 |
| ri | 子组i的极差 |
| m | 子组数 |
| d2(·) | 与括号中指定的值相对应的五偏常量d2值 |
| ni | 子组i中的观测值个数 |
| d3(·) | 与括号中指定的值相对应的无偏常量d3值 |
2. 合并标准差方法
合并标准差 Sp 按一下公式计算：
当子组大小固定时，按以下方式计算 Sp：
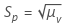
使用无偏常量
默认情况下，使用合并标准差估计 σ 时，Minitab 将应用无偏常量 c4()：
偏倚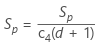 
当子组大小固定时，可按以下方式计算无偏倚的 Sp：
偏倚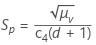
表示法
| 项 | 说明 |
| xij | 第i个子组中的第j个观测值 |
 |
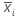子组i的均值 |
| ni | 子组i中的观测值个数 |
| μv | 子组方差的均值 |
| c4(·) | 与括号中指定的值相对应的无偏常量c4值 |
| d | Sp的自由度，计算公式：∑(ni - 1) |
4. Xbar-R控制图中Xbar控制图的方法和公式
1. 描绘点
每个描绘点
代表子组中观测值均值（子组 i）。
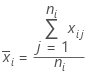
表示法
| 项 | 说明 |
| xij | 第 i 个子组中的第 j 个观测值 |
| ni | 子组 i 中的观测值个数 |
2. 中心线
中心线代表过程均值（μ）。如果没有指定历史值，则 Minitab 使用数据的平均值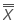 
，计算方式：
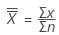
表示法
| 项 | 说明 |
| Σx | 所有单个观测值的总和 |
| Σn | 总观测值个数 |
3. 控制限
1. 控制下限（LCL）
每个子组 i 的控制下限值的计算方式：
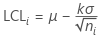
2. 控制上限（UCL）
每个子组 i 的控制下限值的计算方式：
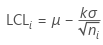
表示法
| 项 | 说明 |
| μ | 过程均值 |
| k | 检验 1 的参数（默认值为3） |
| σ | 过程标准差 |
| ni | 子组 i 中的观测值个数 |
5. Xbar-R控制图中 R 控制图的方法和公式
1. 描绘点
每个描绘点 ri 代表子组 i 的极差。
2. 中心线
每个子组的中心线的值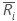
的计算方式：
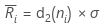
表示法
| 项 | 说明 |
| ni | 子组 i 中的观测值个数 |
| d2(·) | 与括号中指定的值相对应的无偏常量 d2 值 |
| σ | 过程标准差 |
3. 控制限
1. 控制下限（LCL）
每个子组的控制下限值 i 大于等于以下值：
或
LCLi = 0
2. 控制上限（UCL）
每个子组的控制上限值 i 的计算方式：
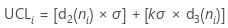
表示法
| 项 | 说明 |
| d2(·) | 与括号中指定的值相对应的无偏常量d2值 |
| ni | 子组i中的观测值个数 |
| σ | 过程标准差 |
| k | 检验1的参数（默认为3） |
| d3(·) | 与括号中指定的值相对应的无偏常量d3值 |
6. 无偏常量d2()、d3()、d4()
d2(N)是正太总体分布（标准差 = 1）中 N 观测值的预期值。因此，如果 r 是正太分布（标准差 = σ）中 N 观测值的样本的极差，则E(r) = d2(N)σ。
d3(N)是正太分布（σ = 1）中 N 观测值的极差的标准差。因此，如果 r 是正太分布（标准差 = σ）中 N 观测值的样本的极差，则stdev(r) = d3(N)σ。
可使用下表查找给定值 N 的无偏常量：
对于从51-100的 N 值，使用 d2(N)以下的近似值：
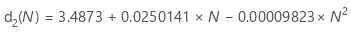
对于从26-100的N值，使用d3(N)和d4(N)的以下近似值：
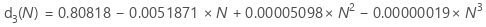
7. 无偏常量c4()和c5()
C4()
C5()
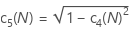
表示法
| 项 | 说明 |
| Γ() | Gamma函数 |
