时间序列模型（三）：指数平滑法
一次移动平均实际上认为近N期数据对未来值影响相同，都加权 1/N；而 N 期以前的数据对未来值没有影响，加权为0。但是，二次及更高次移动平均数的权数却不是 1/N，且次数越高，权数的结构越复杂，但永远保持对称的权数，即两端项权数小，中间项权数大，不符合一般系统的动态性。一般来说历史数据对未来值的影响随时间间隔的增长而递减的。所以，更切合实际的方法应是对各期观测值依时间顺序进行加权平均值作为预测值。指数平滑法可满足这一要求，而且具有简单的递推形式。
指数平滑法根据平滑次数的不同，分为一次指数平滑法、二次指数平滑法、三次指数平滑法等。
1. 一次指数平滑法
1. 预测模型
设时间序列为 y1,y2,...,yt,...，α为加权系数，0<α<1，一次指数平滑公式为：
式（13）是由移动平均公式改进而来的。由式（1）知，移动平均数的递推公式为
2. 加权系数的选择
在进行指数平滑时，加权系数的选择是很重要的。由式（15）看出，α的大小规定了在新预测值中数据和原预测值所占的比重。α越大，新数据占的比重越大，原预测值占的比重越小，反之亦然。若把式（15）改成
上式可以看出，新预测值是根据预测误差对原预测值进行修正得到的。α的大小体现了修正幅度，α越大，修正幅度越大；α越小，修正幅度越小。
若选取 α = 0，则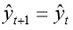
，即下期预测值就等于本期预测值，
