适用于多品种情况的回归控制图
本节针对“不满足同一分布”的“多品种”的情况，介绍一种称为“回归控制图”的特殊控制图技术。
1. 回归控制图原理
针对“多品种”情况，可以采用“回归”技术，对服从不同正太分布的数据进行“预处理”，使不同批次的数据“回归”到满足“同一个分布”的条件，然后采用常规控制图分析经过预处理的数据，确定统计受控状态。
对原始数据进行“回归”预处理后再调用常规控制图的过程称为回归控制图技术。
2. 回归方法一：标准正太处理
1. 数据的“标准正太处理”
2. “标准正太处理”的应用实例
按照式（5-1）将数据转换为标准正太分布后的数据如表 5-5 所示。
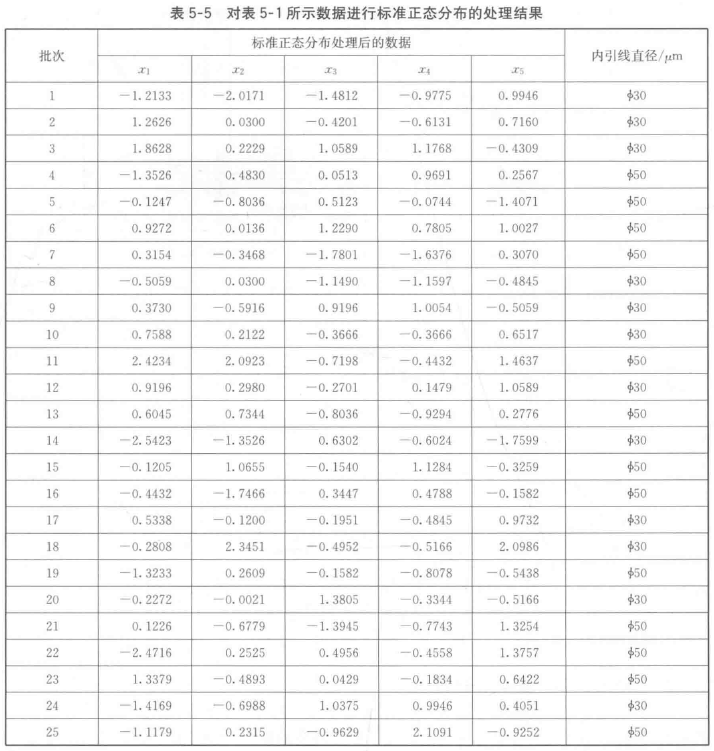
对表5-5中变换后的数据，采用概率纸、直方图、分布拟合3种方法分析，结果如图 5-14。
在正太概率纸中变换后的数据分布基本为一条直线，线性相关系数高达0.997；直方图呈对称性，也可以视为正态分布；分布拟合结果表明，变换后的数据确实服从正太分布。
因此，不同直径内引线的拉力强度数据经过标准正太分布处理后确实服从同一正态分布。
对表5-5数据采用常规控制图分析，得到图5-15。
3. “标准正太处理”技术适用条件
采用式（5-1）将正太分布数据转换为标准正太分布时，首先将每个数据减去该正太分布的均值，再除以该正太分布的标准差。
为了保证转换的精度，在采用式（5-2）计算正太分布的均值和标准差时数据不能太少，不应少于30个。如果少于20个，可信度很差。
为了保证每个品种的数据个数基本满足这一要求，采用“标准正太处理”技术时品种数不能太多，一般不超过3~4个；每批数据个数不少于5个。
3. 回归方法二：“相对偏差”方法
1. “相对偏差”处理技术应用实例
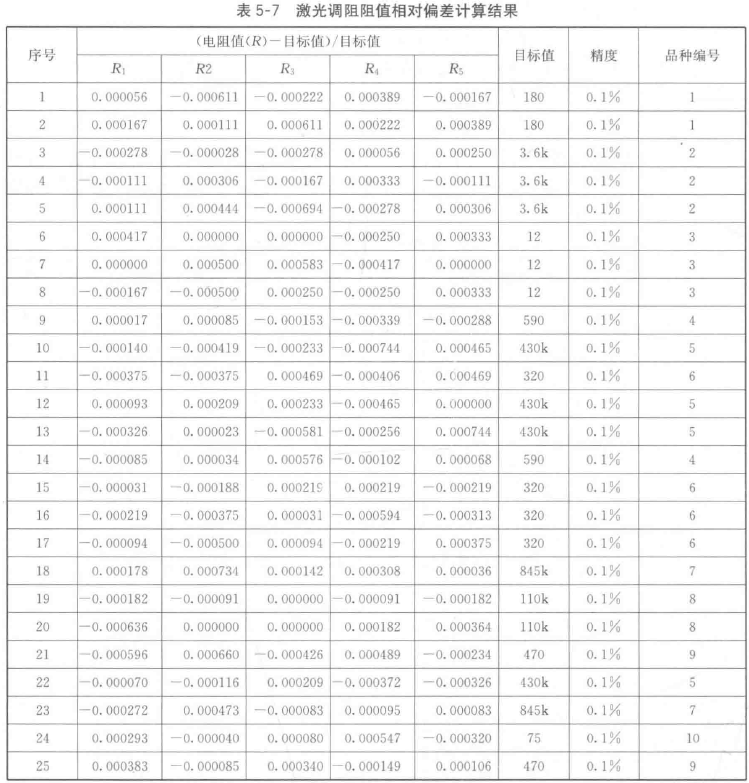
表5-6为25批电阻值数据，表中同时给出目标值、精度要求。由于目标值有10种，是一个品种数较多的多品种情况。
尽管目标值不同，但精度相同，对表5-6中每个阻值按照相对偏差 = （电阻值-目标值）/ 目标值来计算相对偏差数据（表5-7），发现服从同一正太分布。采用正太分布概率纸、直方图和分布拟合结果，如图5-16，相对偏差确实服从同一正太分布。
采用常规图分析相对偏差数据，如图5-17。
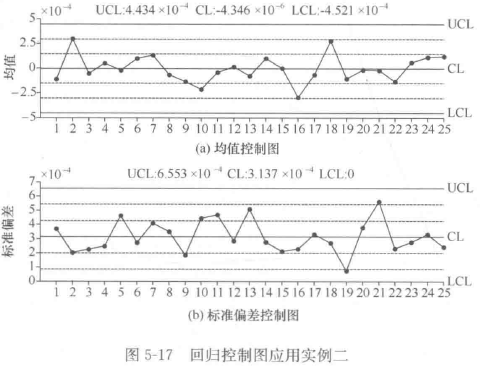
2. “相对偏差”处理技术适用条件
计算相对偏差对数据个数没有限制，因此对品种较多、每个品种数据较少的情况可以选用这种方法。
但实践表明，如果相对偏差较大（超过10%）、不同品种数值范围跨度过大（如电阻值从几欧到几百兆欧），则效果较差。这种情况选用T-K控制图。
4. 关于“双重回归”情况
“回归”技术的核心是对服从不同正太分布的数据采用预处理，使不同批次的数据“回归”到“同一个”分布的条件。上面两种回归处理方法，实际应用中不存在统一的算法，针对不同情况采用不同的回归处理方法。
下面介绍综合上述两种方法的“双重回归”情况。
经历两次归一化处理，又称为“双重回归”。
例：表5-8给出25批电阻数据，从表中看出目标值有9种，2种精度要求，这是采用“双重回归”技术的典型情况。
首先计算每个阻值的相对偏差，然后对属于不同精度要求的相对偏差数据进行“标准正太分布处理”，最后采用常规控制图分析经过两次归一化处理的数据。如图5-18。
