适用于非正太分布数据的控制图
1. 非正太分布数据的控制图分析方法
对于非正太分布数据，采用两种方法使用控制图。
1. 数据转换方法
对非正太分布数据进行控制图分析包括三方面：
（1）确认数据服从的分布
简单方法：概率纸、直方图
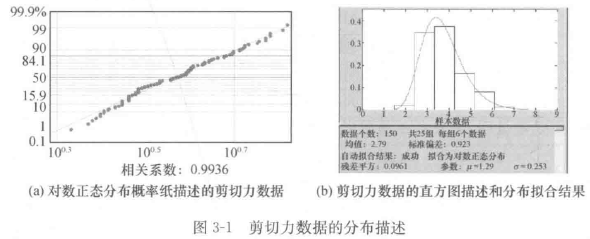
（2）将非正太分布数据转换为正太分布数据
例如：服从对数正太分布的数据，对每个数据取对数，将其转换为正太分布。一般情况，采用数理统计中Box变换技术。
（3）对转换后的数据采用合适的计量值控制图分析。
2. 采用分位数控制图
对非正太分布的情况，也可以采用分位数控制图。
2. 制造过程非正太分布数据控制图实例
下面以图5-1所示，有服从对数正太分布的25批共150个数据。
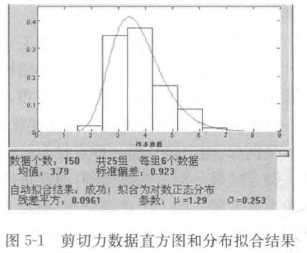
（1）数据转换
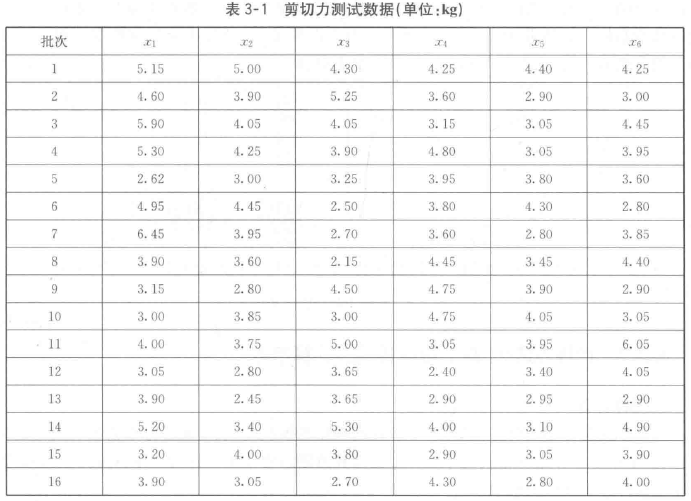
由表3-1所示，数据服从对数正太分布，
对每个数据取对数，产生的数据服从正态分布。结果如表3-2。
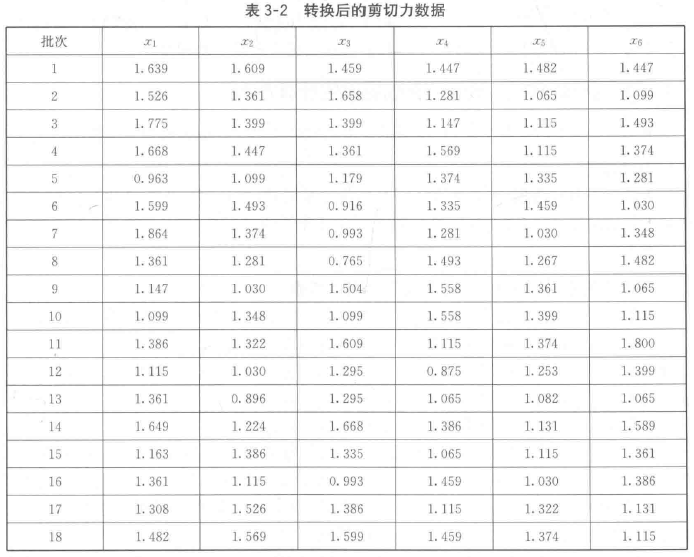
对表3-2中的数据，采用概率纸分析结果如图5-4。在正太概率纸变换后的数据分布基本为一条直线。
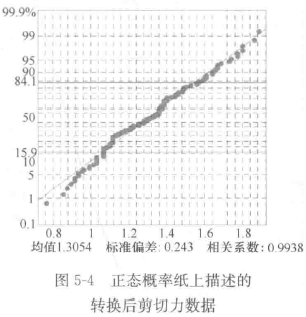
（2）调用控制图
表3-2的数据，满足常规计量值控制图的使用条件，可以采用均值-标准差控制图分析统计受控状态。
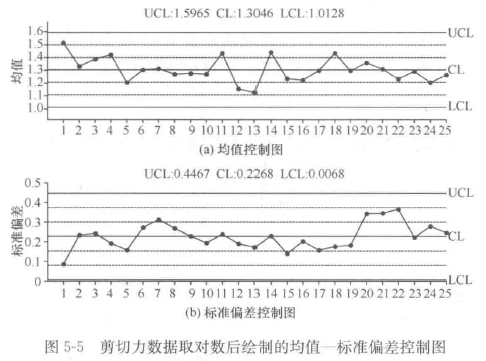
3. 非制造过程中非正太分布数据控制图实例
在非制造过程的SPC评价中，特别是采用单值-移动极差控制图分析时间间隔的情况，会出现非正太分布。
1. 实例一：阀门更换时间数据的控制图分析
（1）测量数据
为了监测一个阀门更换周期是否正常，采用控制图监测阀门失效前正常工作小时数的情况。
如表5-3：
采用概率纸描述阀门工作时间数据，如图5-6。由于数据不在一条直线上，说明时间不服从正太分布。
（2）数据转换
采用Box变换技术，对阀门工作时间y进行变换，将其转换为正太分布。
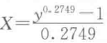
变换后的数据如表5-3所示。采用正太概率纸描述变换后的数据如图5-7所示。
由于数据基本在一条直线上，线性相关系数为0.9862，线性程度较高，说明变换后数据服从正态分布。
（3）控制图分析
采用单值-移动极差控制图分析统计受控状态。
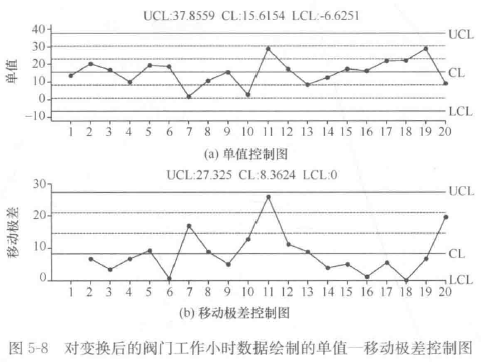
（4）说明
如果不进行数据转换，直接调用单值-移动极差控制图分析，结果如图5-9。
单值控制图和移动极差控制图上均出现失控点。实际失控点并不是因为异常出现失控，而是因为阀门正常工作数小时不满足正太分布。
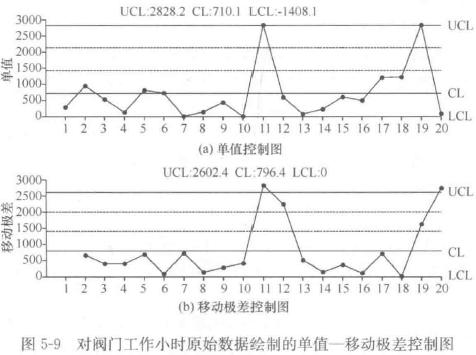
这就说明，对于非正太分布的数据不能直接采用常规计量值控制图进行分析，因为会对结果造成误判。
2. 实例二：谋杀案数据的控制图分析
（1）谋杀案案发间隔时间数据
总共29起谋杀案，每次谋杀案发生的时间间隔如表5-4所示。
采用正太概率纸描述案发生间隔时间数据，如图5-10。可以看出数据不在一条直线上，说明时间间隔数据不服从正太分布。
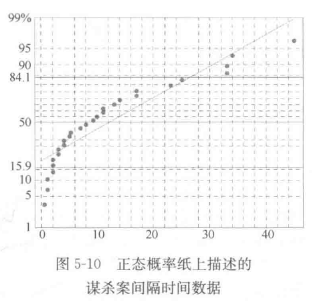
（2）数据变换
采用Box变换技术，对谋杀案间隔时间 y 进行下述变换，可以将其转换为正太分布。
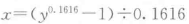
变换后的数据如表5-4。概率纸描述变换后的数据如图5-11。数据基本在一条直线上，线性相关系数高达0.9942。
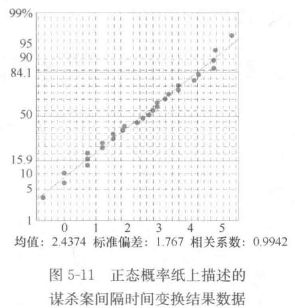
（3）控制图分析
变换后的数据服从正太分布，采用单值-移动极差控制图分析统计受控状态，如图5-12。
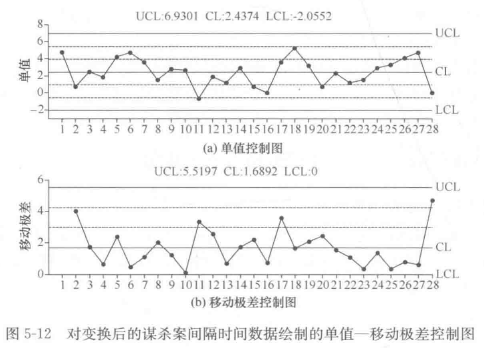
说明谋杀案发生的时间间隔波动正常，不存在异常因素。
（4）说明
对不服从正太分布的谋杀案时间间隔数据，不进行数据转换，直接调用单值-移动极差控制图分析，如图5-13。
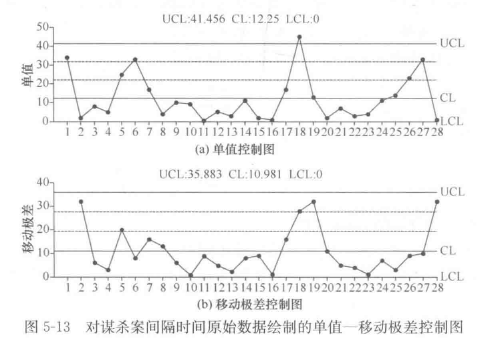
单值控制图上出现了超出控制限的失控点，同时还出现连续9点在中心线同一侧的情况。
实际上失控点并不是出现异常原因导致失控，而是谋杀案时间间隔数据不满足正太分布。
