特殊控制图的基本原理
1. 常规控制图的适用条件
1. 常规计量值控制图的适用条件
采用常规计量值控制图分析时参数满足两个条件：
1. 只有一个参数；
2. 数据完全相互独立，且服从同一正态分布（相互独立、服从正态分布、同一正态分布）。
2. 常规计数值控制图的适用条件
（1）常规计点值控制图适用条件
对计点值缺陷数据，使用常规缺陷数控制图的前提条件是缺陷数服从泊松分布，即每个缺陷数相互独立。
（2）常规计件值控制图的适用条件
对计件值使用不合格品数/不合格品率控制图的前提条件是不合格品数服从二项分布。即每个不合格品的出现是相互独立的。
（3）常规计点值控制图和计件值控制图均采用 3σ 原理确定控制限，实际上是将泊松分布的计点值控制图和适用于二项分布的计件值控制图采用了正太分布近似。
2. 需要采用特殊控制图的典型情况
1. 不满足“正太”分布情况
判断一组数据分布特点直观方法是概率纸和直方图方法。
如图5-1：
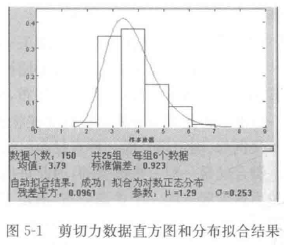
直方图明显不对称，因此不服从正太分布，根据分布拟合结果表明数据服从对数正太分布。
2. 不满足“同一分布”的情况
一般常说的“多品种”问题，不满足“同一分布”。例如：同一车床加工不同直径尺寸的插针，正常情况下同一直径的插针服从同一正太分布，不同直径的插针服从不同正态分布，这就不满足“同一个”分布的要求。
3. 不满足“数据完全相互独立”的情况
（1）不满足“数据完全相互独立”条件的批处理加工情况
（2）不满足“数据完全相互独立”条件的“自相关”数据情况
4. 不满足“只采用一个参数”的情况
例如：金属丝加工，对金属丝同时有直径和抗拉强度两个要求，而且这两个参数具有明显的相关性。 不满足第一个使用条件。
5. 缺陷数很少/合格率很高的高水平工艺情况
平均缺陷数 λ 小于1，不合格品率 p 小于1%，这时泊松分布和二项分布均不能采用正太分布近似，因此不能采用常规计点值控制图和计件值控制图。
6. 缺陷数不满足泊松分布的情况
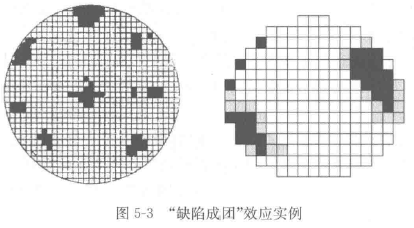
缺陷数不服从泊松分布，例如：半导体器件产生的缺陷并不相互独立，表现为“成团效应”。
图5-3为半导体器件生产中晶圆上不合格管芯分布情况的两个实例。图中黑色为没有功能的费管芯，灰色为参数不合格的管芯。这些不合格管芯出现的位置明显地显示出“成团效应”。
对表现为“成团效应”的缺陷数，采用缺陷成团控制图。
3. 特殊控制图的基本原理
特殊控制图依据的原理与常规控制图一样：
1. 按照正太分布 3σ 原理及其对应的概率值确定控制限。
2. 常规控制图的判断规则完全适用于特殊控制图。
