SPC与常规控制图
这篇随笔介绍SPC(Statistical Process Control)概念和控制图的基本原理,剖析在实践中经常将加工结果是否合格与生产过程是否处于统计受控状态混淆的问题。
1. SPC基本概念
1. 结果起伏变化的两类原因
(1)随机原因
实际生产中,即使受控因素保持不变,人(Man)、机(Machine)、料(Material)、法(Method)、环(Environment)、测(Measurement)这6个因素(又称5M1E),绝对保持不变不可能,必然存在随机扰动。
随机原因引起的波动有以下几个特点:
1. 起伏波动程度较小。
2. 有一定的统计规律。如像镀层厚度这类计量值参数数据呈现正态分布。而像镀件表面的疵点缺陷数这类计数值参数服从泊松分布。
(2)异常因素和可识别原因
异常原因大体包括设备运转失灵、刀具磨损、过失误差、设备刚维修后的状态变化、原材料改变等。
异常原因引起的波动有以下几个特点:
1. 并不总是存在。
2. 变化幅度异常大,或者变化幅度不大,但变化呈现某种规律。如逐渐增大或减少。
2. “统计受控”的概念与SPC的作用
(1)工艺统计受控的含义
过程只存在随机原因引起的起伏,不存在异常原因,则称过程处于统计受控状态。存在异常原因的影响,称过程处于失控状态。
在SPC实践中,将生产过程是否处于统计受控状态与加工结果是否规范等同起来,是一种不正确的认识。
(2)SPC作用
SPC作用是对数据采用“控制图”进行定量分析,确保过程一直处于受控状态。是一项“事先预防”技术。
2. “统计受控”与“加工结果是否合格”的关系
“工艺统计受控”只是考虑生产过程是否存在“异常原因”,这是SPC技术解决的问题。加工结果是否合格这是工序能力指数评价要解决的问题。不能将两者混为一谈。
制造过程存在受控和失控,工艺水平存在高和低,在实际制造过程中,下述4种状态都是可能存在的。
1. 受控状态、产品合格
2. 失控状态、产品合格
3. 受控状态、产品不合格
4. 失控状态、产品不合格
3. 控制图的结构和作用
SPC过程中判断是否处于统计受控状态的基本工具是控制图。
1. 控制图的结构组成
图4-2是采用“均值-标准偏差控制图”分析是否处于统计受控状态。
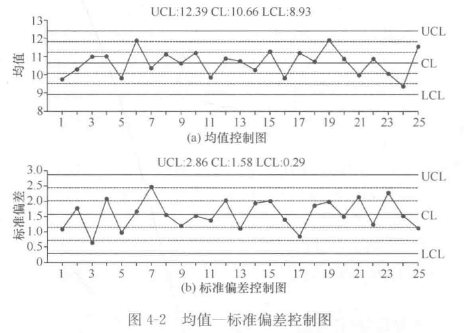
在图4-2(a)所示的均值控制图中,用折线连接的是每批数据的均值。UCL(Upper Control Limit)为上控制限、LCL(Lower Control Limit)为下控制限、CL(Center Line)为中心线。可用于从中心值判断波动起伏中是否存在“异常原因”。
在图4-2(b)所示的标准偏差控制图中,每个数据点是每批数据的标准差。可用于从分散性判断波动起伏中是否存在“异常原因”。
由上可见,控制图是在具有控制限的坐标系中,用折线表示特征值(如均值、标准差)随次数的变化情况。分析数据起伏变化的原因中是否存在异常原因,从而判断生产过程是否处于统计受控状态。
2. 控制图依据的数学原理
计算控制限以及建立受控/失控判断规则依据的以下原理。
(1)中心极限定理与工艺参数的正太分布
根据中心极限定理,如果某一质量特性是许多随机因素的综合,而没有显著的非正太因素,则该质量特性参数服从正太分布。
(2)特征值的正态性
即使母体不是正态分布,其许多样本特征(一般要求每批样本数n不小于5),如均值等,近似为正太分布。
这就是为什么采用控制图时要求每批数据的个数最好不小于5。
(3)正太分布特征值的统计特性
实施SPC涉及正太分布的多种特征参数。如果母体服从均值为μ,标准偏差为σ的正太分布,即X~N(μ, σ2),若抽取容量为n的子样
(4)小概率事件原理
出现小概率事件,认为假设不成立。控制图中控制限的计算以及判断生产过程是否处于统计受控制状态的基本出发点都是基于“小概率事件”。
4. 控制限的计算原理
1. 3σ法则
(1)根据“3σ法则”确定的控制限
若参数Y服从均值为μ、标准差为σ的正态分布,即Y~N(μ, σ2),根据数理统计原理,随机变量Y取值在(μ±3σ)范围的比例为99.73%。或者说,Y取值超出这一范围的概率仅为0.0027,为小概率,通常情况下不会发生。因此可以采用下式(4-1)确定中心线、上、下控制限:
UCL = μ+3σ
CL = μ
LCL = μ - 3σ
我国标准“GB/T 4091常规控制图”采用“3σ法则”计算控制限。
(2)根据“3σ法则”确定控制限对应的分位数
根据“3σ法则”,参数特征小于下控制限 (μ-3σ) 的概率均为0.00135,因此下控制限就是参数特征值对应的分布的0.00135分位数。
参数特征值大于上控制限(μ+3σ)的概率也为0.00135,则参数特征值小于上控制限(μ+3σ)的概率为(1-0.00135)=0.99865,因此,上控制限就是参数特征值所对应分布的0.99865分位数。
2. 概率值(0.001)法
概率值0.001对应于工艺参数特征值大于(μ+3.09σ)的概率或者特征值小于(μ-3.09σ)的概率。相当于将“3σ法则”中的3σ改为3.09σ。
5. 工艺过程受控/失控状态的判断规则
下面基于“小概率事件原理”介绍受控/失控状态的判断方法,并介绍 “GB/T 4091常规控制图” 规定的一组判断规则。
1. 判断规则的基本原理
(1)是否有数据点超出控制限,并不是判断是否处于统计受控状态的唯一准则。
(2)从“小概率事件在一般情况下不应出现”的原理出发,推导出多条判断规则。如果发生了,表示失控。
2. 统计受控状态的判断规则
根据“正常情况下小概率事件不应出现”的原理,可以推到出多条判断规则。
国家标准“GB/T 4091常规控制图”给出下面8条基本判断规则。即如果出现下述情况之一,则判断生产失控。
为了便于理解,将控制图上、下控制限范围分为6个区间,如图4-3:
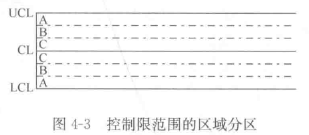
由于上、下控制限分别对应中心线CL+3σ以及CL-3σ,因此每个区间对应一个σ。
(1)规则1:控制图上有一个点位于控制限以外。
说明一:超出控制限的数据点,说明控制参数发生了较大幅度的波动,使得该过程出现失控状态,因此这事应该选择使用的一条基本判断规则。
说明二:针对数据点超出控制限的判断规则如下,其中括号内的值是相应事件发生的概率值。
若控制图上有“一部分”数据点超出控制限,则该工艺过程失控。“一部分”数据点是指如下情况:
连续25个数据点中至少有一个点在控制限以外(0.0654);
连续35个数据点中至少有两个点在控制限以外(0.0041);
连续100个数据点中至少有三个点在控制限以外(0.0025)。
按照这一判断规则,并非只要有数据点超出控制限就表示工艺失控。例如,若连续35个数据点中只有第26号数据点超出控制限,按照上述判断规则,并不判断工艺失控。
下面7条规则,数据点均为超出控制限,但是只要出现相应的小概率事件,也应判断工艺失控。
(2)规则2:连续9点落在中心线的同一侧。
(3)规则3:连续6点递增或递减。
说明:当零部件/材料因磨损/耗减到一定程度需要更换时,控制图上将会出现连续多点递增或者递减的情况,因此对于这类工序,应选规则3。
(4)规则4:连续14点相邻点交替上下。
(5)规则5:连续3点中有两点落在中心线同一侧的B区以外。
(6)规则6:连续5点中有4点落在中心线同一侧的C区以外。
(7)规则7:连续15点落在中心线两侧的C区内。
(8)规则8:连续8点落在中心线两侧且无一点在C区内。
上述规则适用于所有的控制图。
6. 常规控制图的分类
1. 参数的类别
根据工艺参数统计属性的不同,将工艺分为两类。
(1)计量值:指取值是连续变化的参数,如车床加工的零件直径、电镀件的镀层厚度、半导体器件生产中掺杂方块电阻、键合拉力强度等。
对计量值参数,通常用中心值和分散性描述其参数分布特性。中心值的变化情况可用均值或中位数描述。参数的分散情况用标准差或极差描述。
(2)计数值:指只能取离散的参数,如印制电路板上的疵点数、键合丝断丝根数、电视机屏幕上的针孔数、半导体器件生产中的封装不合格品格数等。
计数值又分为不合格品数、不合格品率(统称为计件值)和缺陷数以及单位产品中缺陷数(统计为计点值)共4类。
2. 常规控制图的类型
常规控制图分为计量值控制图和计数值控制图两类。
计量控制图根据表征参数中心值变化情况分为均值控制图和中位数控制图,以及表征参数分散情况下的标准差S控制图和极差R控制图。实际生产中存在每批数据只能采集一个数据的情况,采用单值-移动极差(X-Rs)控制图。
国家标准GB4091涉及4种常用的常规计量值控制图,如表4-1:

上表中,计数值控制图(根据计件值为对象)又分为不合格品数np控制图和不合格品率p控制图,以及(根据计点值为对象)分为c控制图和u控制图。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号