方差分析(One-way ANOVA)
举例:饮料的颜色共有四种,分别为橘黄色、粉色、绿色和无色透明。这四种饮料的营养含量、味道、价格、包装等可能影响销售量的因素全部相同,先从地理位置相似、经营规模相仿的五家超级市场上收集了前一期该种饮料的销售量情况,见表1:
| 超市 | 无色 | 粉色 | 橘黄色 | 黄色 |
| 1 | 26.5 | 31.2 | 27.9 | 30.8 |
| 2 | 28.7 | 28.3 | 25.1 | 29.6 |
| 3 | 25.1 | 30.8 | 28.5 | 32.4 |
| 4 | 29.1 | 27.9 | 24.2 | 31.7 |
| 5 | 27.2 | 29.6 | 26.5 | 32.8 |
| 合计 | 136.6 | 147.8 | 132.2 | 157.3 |
分析饮料的颜色是否对销售产生影响。
1. 方差分析原理
ANOVA叫做方差分析,目的是检验每个组的平均数是否相等。
而实现这个目的的手段是通过方差的比较(即考察数据的差异),而差异的产生来自两个方面。一方面是由因素中的不同水平造成的,称之为系统差异(系统性误差)。如:饮料的不同颜色带来的不同销量。另一方面是由抽取样本时的随机性产生,称之为随机性差异(随机性误差)。如:相同颜色的饮料在不同的商场销量也不同。
两个方面的差异可以用两个方差来计算。
组间方差,即水平之间的方差,是衡量不同总体下各个样本之间差异的方差。在组间方差里,既包括系统性误差,也包括随机性误差。
如:在表1中,不同颜色的饮料在不同地点(超市)产生销量之间的差异既有系统性误差(人对不同颜色的偏爱)也有随机性误差(抽样的随机性),不同颜色的饮料在不同地点产生销售之间的方差即为组间方差。
组内方差,即水平内部的方差,是衡量同一总体下样本数据的方差。在组内方差里,只有随机性差异。
如:在表1中,同一颜色的饮料在不同地点产生销量之间的差异是随机性误差。同一颜色的饮料在不同地点产生销量之间的方差即为组内方差。
如果饮料的不同颜色对销量无影响,那仅有随机性误差,此时,组间方差与组内方差比值接近于1。如果颜色对销售有影响,组间方差既包括随机性误差,也包括系统性误差,比值大于1。
组间方差与组内方差的比值大到某种程度,可以作出判断,不同水平之间存在显著性差异。方差分析就是通过不同方差的比较,作出接受原假设或拒绝原假设的判断。
2. 方差分析思路
令μ1,μ2,μ3,μ4分别为4种颜色饮料的平均销售量,检验它们是否相等。不相等,意味不同颜色的饮料来自不同的总体,表明颜色对销售量有影响;反之,无影响。
3. 计算分析
1. 建立假设
ANOVA原假设(零假设):H0:μ1=μ2=μ3=μ4;假设颜色对销售量没有影响。
备择假设H1:μ1,μ2,μ3,μ4不全相等;即假设颜色对销售量有影响。
2. 计算水平均值
无色饮料销售量均值 = 136.6÷5=27.32
粉色饮料销售量均值=147.8÷5=29.56
桔黄色饮料销售量均值=132.2÷5=26.44
绿色饮料销售量均值=157.3÷5=31.46
3.计算全部观察值的总均值
总样本的平均数 = (136.6+147.8+132.2+157.3)÷20=28.695
4. 计算离差平方和

5. 构造统计量并计算检验统计量的样本值
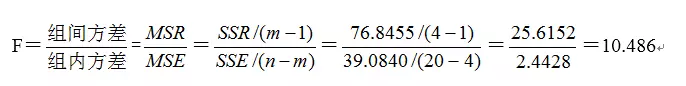
6. 确定检验规则、列出方差分析表、作出统计决策
P-值规则:根据算得的检验统计量的样本值(F值)算出P-值 = 0.000466。由于P-值 = 0.000466 < 显著水平标准 = 0.05,所以拒绝 H0,接受备择假设 H1,即通过检验知,µj不全相等。说明饮料的颜色对销售量有显著影响。
临界值规则:根据给定的显著水平 a = 0.05,查表得临界值为3.24。因为 F = 10.486 > 3.24,检验统计量的样本值落入拒绝域,所以拒绝 H0,接受备择假设 H1。
显著水平:举例说明:某药品商宣传能治愈某病的概率是90%。(即原假设)一个医生不相信宣传,于是做实验验证,15人治好11人。原本15人应治好13.5人。那么宣传是不是有欺骗性。
用假设性检验来验证(采用显著性水平为5%检验),假设这15人服从二项分布,P(X<=11)的概率等于5.6%,大于显著性水平。而我们的显著性水平是5%,也就是说小于5%的是小概率事件,而治愈11人不是小概率事件,所以没有证据证明药品商骗人。所以接受他的宣传(接受原假设),即治愈率90%。
15人治好9人,计算得到p值小于5% ,这个时候处于拒绝域。(小于5%是小概率事件,几乎不可能遇到,怎么刚好让我遇到,所以有足够证据证明是虚假宣传),所以采用备选假设,推翻原假设。
P-值大于显著水平,支持原假设,F值大于临界值(由显著水平得到),拒绝原假设。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号