朴素贝叶斯法

朴素贝叶斯（Nave Bayes）法是基于贝叶斯定理与特征条件独立假设的分类算法。它的思想可以概括为先验概率+数据=后验概率。

1.朴素贝叶斯模型

下面是分类模型样本：

假设有m个样本，每个样本有n个特征，特征输出有K个类别，定义为

从样本得到朴素贝叶斯的先验分布，

接着得到条件概率分布，

然后用贝叶斯公式得到X和y的联合分布P(X, y)：

因为P(Y=C_k)比较容易通过最大似然法求出，得到P(Y=C_k)就是类别C_k 在训练集里面出现的频数。但是P(X₁=x₁, X₂=x₂, ... X_n=x_n| Y=C_k)是个复杂的n个维度的条件分布，很难求出。朴素贝叶斯在这里做了一个大胆的假设，即X的n个维度之间相互独立，得出：

从上式看出，很难的条件分布大大简化了。如果特征之间不独立怎么办？那就尽量不适用朴素贝叶斯模型。这就是贝叶斯模型的选择。

 

最后回到要解决的问题，我们的问题是给定测试集的一个新样本特征，我们如何判断它属于哪个类型？

既然是贝叶斯模型，当然是后验概率最大化来判断分类了。我们只要计算出所有的K个条件概率 ，然后找出最大的条件概率对应的类别，就是朴素贝叶斯的预测。

 

 

2.朴素贝叶斯的推断过程

预测的类别 C_result 是使 P(Y=C_k|X=X^(test))最大化的类别，数学表达式为：

由于对所有的类别计算 P(Y=C_k|X=X^(test))时，上式分母是一样的，都是 P(X=X^(test))，因此，我们的预测公式简化为：

接着利用朴素贝叶斯的独立性假设，得到朴素贝叶斯公式：

 

 

 

 

 

 

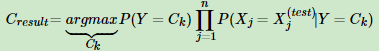
来自：刘建平