AdaBoost 算法

集成学习

随机森林

AdaBoost 算法

提升树

梯度提升树（GBDT）

XGBoost


目录


在 \(Boosting\) 系列算法中，最具代表的是 \(AdaBoost\) 算法。该算法即可用于分类，也可用于回归。


一、AdaBoost 分类算法

假设二分类训练集

\[T=\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\} \]

\(x_i \in \mathcal{X} \subseteq \pmb{R^n}\)（\(n\) 维），\(y_i \in \mathcal{Y} = \{-1,1\}\)，



1. 算法流程

输入：\(T=\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\}\)，\(x_i \in \pmb{R^n}\)（\(n\) 维），\(y_i \in \{-1,1\}\)，弱学习器算法；

输出：最终分类器 \(G(x)\)。

① 初始化权值

\[D_1 = (\omega_{11},...\omega_{1i},...\omega_{1N}), \ \ \ \ \omega_{1i} = \frac{1}{N}, \ \ \ \ i=1,2,...,M \]

② 对 \(m = 1,2,...M\)

​ (a) 使用权值分布 \(D_m\) 的训练集学习，得到基本分类器

\[G_m(x)\to \{-1,1\} \]

​ (b) 计算 \(G_m(x)\) 的分类误差率

\[\tag{1} e_m = \sum_{i=1}^{M} P(G_m(x_i) ≠ y_i) = \sum_{i=1}^{N} \omega_{mi}I(G_m(x_i)≠y_i) \]

​ (c) 计算 \(G_m(x)\) 的系数

\[\tag{2} \alpha_m = \frac{1}{2} log \frac{1-e_m}{e_m} \]

这里的对数为自然对数。

​ (d) 更新权值分布

\[\begin{align} \tag{3} & D_{m+1} = (\omega_{m+1,1},...,\omega_{m+1,i},...,\omega_{m+1,N}) \\ \tag{4} & \omega_{m+1,i} = \frac{\omega_{mi} e^{(-\alpha_m \ y_i \ G_m \ (x_i))}} {Z_m} \\ \tag{5} & Z_m = \sum_{i=1}^{N} \omega_{mi} e^{(-\alpha_m \ y_i \ G_m \ (x_i))} \end{align} \]

\(Z_m\) 是规范化因子。

③ 构建基本分类器的线性组合

\[\tag{6} f(x) = \sum_{m=1}^{M} \alpha_m G_m(x) \]

最终分类器

\[\tag{7} G(x) = sign(f(x)) \\ \]


以上是 \(AdaBoost\) 二分类问题的算法流程，对于 \(AdaBoost\) 多分类问题，原理与二分类类似，最主要区别在基分类器的系数上。比如 \(AdaBoost \ \ \ SAMME\)​ 算法，它的基分类器系数

\[\alpha_m = \frac{1}{2} log \frac{1-e_m}{e_m} + log(R-1) \]

其中 \(R\) 为类别数。如果是二分类，\(R=2\)。



2. 算法分析

① \(I(G_m(x_i) ≠ y_i)\) 中，当 \(G_m(x_i) = y_i\) 时为 \(0\)，\(G_m(x_i) ≠ y_i\) 时为 \(1\)。

② \(0 \leqslant e_m \leqslant 0.5\)

因为当 \(e_m \geqslant 0.5\) 会自动转换为 \(e_m \leqslant 0.5\)。

\(x\) 0 1 2 3
\(y\) 1 1 1 1
\(G_m(x)\) -1 -1 -1 1
错误 错误 错误 正确

自动转换为：

\(x\) 0 1 2 3
\(y\) 1 1 1 1
\(-G_m(x)\) 1 1 1 -1
正确 正确 正确 错误

③ 由下图可得，\(\alpha_m\) 随 \(e_m\) 减小而增大。

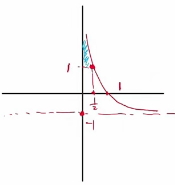
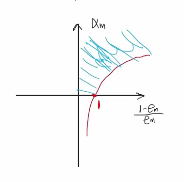
\[0 \leqslant e_m \leqslant 0.5 \Longrightarrow 2 \leqslant \frac{1}{e_m} \Longrightarrow 1 \leqslant \frac{1}{e_m} - 1 \Longrightarrow 0 \leqslant log \frac{1-e_m}{e_m} \Longrightarrow 0 \leqslant \alpha_m \]



3. 算法实例

例 \(1\)：给定训练集，用 \(AdaBoost\) 算法学习一个强分类器。

序号 1 2 3 4 5 6 7 8 9 10
\(x\) 0 1 2 3 4 5 6 7 8 9
\(y\) 1 1 1 -1 -1 -1 1 1 1 -1

解：① 初始化权值

\[D_1 = (\omega_{11},\omega_{12},...\omega_{110}) \\ \omega_{1i} = 0.1, \ \ \ \ i=1,2,...,M \]


② 对 \(m = 1\)

​ (a) 使用权值分布 \(D_1\) 的训练集学习，阈值 \(v=2.5\) 时分类误差率最大，得到基本分类器

\[G_1(x) = \begin{cases} 1, & x<2.5 \\ -1, & x>2.5 \end{cases} \]

​ (b) \(G_1(x)\) 的分类误差率 \(e_1 = P(G_1(x_i) ≠ y_i) = 0.3\)。

​ (c) \(G_1(x)\) 的系数：\(\alpha_1 = \frac{1}{2} log \frac{1-e_1}{e_1} = 0.4236\)

​ (d) 更新权值分布：

\[\begin{aligned} & D_2 = (\omega_{21},...,\omega_{2i},...\omega_{210}) \\ \\ & \omega_{2i} = \frac{\omega_{1i} e^{(-\alpha_1 y_i G_1(x_i))}} {Z_1} \\ \\ & D_2 = (0.07143,0.07143,0.07143,0.07143,0.07143,0.07143,0.16667,0.16667,0.16667,0.07143) \\ \\ & f_1(x) = 0.4236 G_1(x) \end{aligned} \]

分类正确的样本权重更新计算：\(w_{1i} e^{(-\alpha_1 y_i G_1(x_i))} = 0.1 \times e^{(-0.4263 \times 1 \times 1)} = 0.065469\)

分类错误的样本权重更新计算：\(w_{1i} e^{(-\alpha_1 y_i G_1(x_i))} = 0.1 \times e^{(0.4263 \times 1 \times 1)} = 0.152745\)

\(Z_1 = 0.065469 \times 7 + 0.152748 \times 3 = 0.916515\)

分类正确的样本更新后的权重：\(\omega_{2i} = \frac{0.065469}{0.916515} = 0.071432\)

分类错误的样本更新后的权重：\(\omega_{2i} = \frac{0.152745}{0.916515} = 0.166659\)

分类器 \(sign[f_1(x)]\) 有三个误分类点。


对 \(m = 2\)

​ (a) 使用权值分布 \(D_2\) 的训练集学习，阈值 \(v=8.5\) 时分类误差率最大，得到基本分类器

\[G_2(x) = \begin{cases} 1, & x<8.5 \\ -1, & x>8.5 \end{cases} \]

​ (b) \(G_2(x)\) 的分类误差率 \(e_2 = P(G_2(x_i) ≠ y_i) = 0.2143\)。

​ (c) \(G_2(x)\) 的系数：\(\alpha_2 = \frac{1}{2} log \frac{1-e_2}{e_2} = 0.6496\)

​ (d) 更新权值分布：

\[\begin{aligned} & D_3 = (0.0455,0.0455,0.0455,0.1667,0.1667,0.1667,0.1060,0.1060,0.1060,0.0455) \\ & f_2(x) = 0.4236G_1(x) + 0.6496G_2(x) \end{aligned} \]

分类器 \(sign[f_2(x)]\) 有三个误分类点。


对 \(m = 3\)

​ (a) 使用权值分布 \(D_3\) 的训练集学习，阈值 \(v=5.5\) 时分类误差率最大，得到基本分类器

\[G_3(x) = \begin{cases} 1, & x<5.5 \\ -1, & x>5.5 \end{cases} \]

​ (b) \(G_3(x)\) 的分类误差率 \(e_3 = P(G_3(x_i) ≠ y_i) = 0.1820\)。

​ (c) \(G_3(x)\) 的系数：\(\alpha_3 = \frac{1}{2} log \frac{1-e_3}{e_3} = 0.7514\)

​ (d) 更新权值分布：

\[\begin{aligned} & D_3 = (0.125,0.125,0.125,0.102,0.102,0.102,0.065,0.065,0.065,0.125) \\ & f_3(x) = 0.4236G_1(x) + 0.6496G_2(x) + 0.7514G_3(x) \end{aligned} \]

分类器 \(sign[f_2(x)]\) 的误分类点为0。


于是最终分类器

\[G(x) = sign[f_3(x)] = sign[0.4236G_1(x) + 0.6496G_2(x) + 0.7514G_3(x)] \]



二、AdaBoost 分类算法误差分析

\(AdaBoost\) 能在学习过程中不断减少训练误差，即训练集上的分类误差率。

定理 \(1\)： \(AdaBoost\) 算法最终分类器的训练误差界为

\[\tag{8} \frac{1}{N} \sum_{i=1}^{N} I(G(x_i)≠y_i) \leqslant \frac{1}{N} \sum_{i}e^{(-y_if(x_i))} = \prod_{m} Z_m \]

\(G(x)\)、\(f(x)\)、\(Z_m\) 分别由式 \((7)\)、\((6)\)、\((5)\) 给出。

证明：当 \(G(x_i)≠y_i\) 时，\(y_if(x_i)<0\)，因而 \(e^{(-y_if(x_i))} \geqslant 1\)。推到出前半部分。

后半部分推到用到 \(Z_m\) 的定义式 \((5)、(4)\) 的变形：

\[\omega_{mi} e^{(-\alpha_m \ y_i \ G_m \ (x_i))} = Z_m \omega_{m+1,i} \]

\[\begin{aligned} \frac{1}{N} \sum_{i} \exp \left(-y_{i} f\left(x_{i}\right)\right) &=\frac{1}{N} \sum_{i} \exp \left(-\sum_{m=1}^{M} \alpha_{m} y_{i} G_{m}\left(x_{i}\right)\right) \\ &=\sum_{i} w_{1 i} \prod_{m=1}^{M} \exp \left(-\alpha_{m} y_{i} G_{m}\left(x_{i}\right)\right) \\ &=Z_{1} \sum_{i} w_{2 i} \prod_{m=2}^{M} \exp \left(-\alpha_{m} y_{i} G_{m}\left(x_{i}\right)\right) \\ &=Z_{1} Z_{2} \sum_{i} w_{3 i} \prod_{m=3}^{M} \exp \left(-\alpha_{m} y_{i} G_{m}\left(x_{i}\right)\right) \\ &=\cdots \\ &=Z_{1} Z_{2} \cdots Z_{M-1} \sum_{i} w_{M i} \exp \left(-\alpha_{M} y_{i} G_{M}\left(x_{i}\right)\right) \\ &=\prod_{m=1}^{M} Z_{m} \end{aligned} \]

这说明，每一轮选取适当的 \(G_m\) 使 \(Z_m\) 最小，从而使训练误差下降最快。

定理 \(2\)： 二分类问题 \(AdaBoost\) 的训练误差界

\[\begin{aligned} \prod_{m=1}^{M} Z_{m} & = \prod_{m=1}^{M}\left[2 \sqrt{e_{m}\left(1-e_{m}\right)}\right] \\ & = \prod_{m=1}^{M} \sqrt{\left(1-4 \gamma_{m}^{2}\right)} \\ & \leqslant \exp \left(-2 \sum_{m=1}^{M} \gamma_{m}^{2}\right) \end{aligned} \]

推论 1：如果存在 \(\gamma>0\)，对所有 \(m\) 有 \(\gamma_m \geqslant \gamma\)，则

\[\frac{1}{N} \sum_{i=1}^{N} I(G(x_i) ≠ y_i) \geqslant e^{(e^{-2M \gamma^2} \ \ \ )} \]

表明此条件下 \(AdaBoost\) 的训练误差是以指数速率下降。

注意：\(AdaBoost\) 不需要知道下界 \(\gamma\)。该算法具有适应性，即能适应弱分类器各自的训练误差。这是它名称的由来，\(Ada\) 是 \(Adaptive\) 的简写。



三、AdaBoost 分类算法解释

\(AdaBoost\) 分类算法还有另一种解释，可认为 \(AdaBoost\) 分类算法是模型为加法模型、损失函数为指数函数、学习算法为前向分步算法的二分类学习算法。



1. 前项分布算法

加法模型

\[\tag{9} f(x) = \sum_{m=1}^{M} \beta_mb(x;\gamma_m) \]

\(b(x;\gamma_m)\) 为基函数，\(\gamma_m\) 为基函数的参数，\(\beta_m\) 为基函数的系数。显然，式 \((6)\) 是加法模型。

在给定训练集及损失函数 \(L(y,f(x))\) 的条件下，学习加法模型 \(f(x)\)​ 成为经验风险极小化即损失函数极小化问题：

\[\tag{10} \underset{\beta_m \ ,\gamma_m}{min} \ \sum_{m=1}^{N} L(y_i, \sum_{m=1}^{M} \beta_m b(x_i;\gamma_m)) \]

前向分步算法思想：因为学习的是加法模型，如果能够从前向后，每一步只学习一个基函数及其系数，逐步逼近优化目标函数式，那么就可以简化优化的复杂度。具体地，每步只需优化如下损失函数：

\[\tag{11} \underset{\beta,\gamma}{min} \sum_{i=1}^{N} L(y_i,\beta b(x_i;\gamma)) \]

给定训练集 \(T = \{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\}\)，\(x_i \in \mathcal{X} \subseteq \pmb{R^n}\)（\(n\) 维），\(y_i \in \mathcal{Y} = \{-1,1\}\)。损失函数 \(L(y,f(x))\) 和基函数的集合 \(\{b(x;\gamma)\}\)，学习加法模型 \(f(x)\) 的前向分步算法如下。



前向分布算法：

输入：训练集 \(T = \{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\}\)，损失函数 \(L(y,f(x))\) 和基函数集 \(\{b(x;\gamma)\}\)；

输出：加法模型 \(f(x)\)。

① 初始化 \(f_0(x)=0\)；

② 对 \(m=1,2,...,M\)

​ (a) 极小化损失函数

\[(\beta_m,\gamma_m) = arg \underset{\beta,\gamma}{min} \sum_{i=1}^{N} L(y_i,f_{m-1}(x_i) + \beta b(x_i;\gamma)) \]

得到参数 \(\beta_m,\gamma_m\)。

​ (b) 更新

\[f_m(x) = f_{m-1}(x) + \beta_m b(x;\gamma_m) \]

③ 得到加法模型

\[f(x) = f_M(x) = \sum_{m=1}^{M} \beta_m b(x;\gamma_m) \]

这样，前向分步算法将同时求解从 \(m=1\) 到 \(M\) 所有参数 \(\beta_m,\gamma_m\) 的优化问题简化为逐次求解各个 \(\beta_m,\gamma_m\) 的优化问题。



2. 前向分步算法与 AdaBoost 分类算法

定理 \(3\)：\(AdaBoost\) 分类算法是前向分布算法的特例。这时，模型是由基本分类器组成的加法模型，损失函数是指数函数。

求证：\(AdaBoost\) 算法基分类器的系数为 \(\alpha_m = \frac{1}{2}log\frac{1-e_m}{e_m}\)。

证明：假设经过 \(m-1\) 轮迭代，得到弱分类器 \(f_{m-1}(x)\)，根据前向分布算法，有：

\[f_m = f_{m-1}(x) + \alpha_m G_m(x) \]

\(AdaBoost\) 的损失函数是指数损失，则有：

\[L = \sum_{i=1}^{N}e^{(-y_i \ f_m \ (x_i))} = \sum_{i=1}^{N}e^{(-y_i \ (f_{m-1} \ \ \ (x_i) + \alpha_m \ G_m))} \]

因为 \(f_{m-1}(x)\) 已知，所以将其移到前面：

\[L = \sum_{i=1}^{N} \bar{w}_{m,i} \ e^{(-y_i \ \alpha_m \ G_m \ (x_i))} \]

其中，\(\bar{w}_{m,i} = e^{(-y_i \ (f_{m-1} \ \ (x)))}\) 是每轮迭代的样本权重，证明化简如下：

\[\begin{aligned} \bar{w}_{m,i} & = e^{(-y_i \ (f_{m-1} \ \ \ (x_i) + \alpha_{m-1} \ \ \ G_{m-1} \ \ \ (x_i)) )} \\ & = \bar{w}_{m-1,i} \ e^{(-y_i \ \alpha_{m-1} \ \ \ G_{m-1} \ \ \ (x_i))} \end{aligned} \]

继续化简 \(L\)：

\[\begin{aligned} L & = \sum_{i=1}^{N} \bar{w}_{m,i} \ e^{(-y_i\ \alpha_i\ G_m \ (x_i))} \\ \\ & = \sum_{y_i = G_m \ (x_i)} \bar{w}_{m,i}\ e^{-\alpha_m} + \sum_{y_i ≠ G_m \ (x_i)} \bar{w}_{m,i}\ e^{\alpha_m} \\ \\ & = \sum_{i=1}^{N} \bar{w}_{m,i} \left( \frac{\sum_{y_i = G_m \ (x_i)} \ \bar{w}_{m,i}}{\sum_{i=1}^{N} \ \bar{w}_{m,i}} \ e^{-\alpha_m} + \frac{\sum_{y_i ≠ G_m \ (x_i)} \ \bar{w}_{m,i}}{\sum_{i=1}^{N} \ \bar{w}_{m,i}} \ e^{\alpha_m} \right) \end{aligned} \]

重写 \(L\)：

\[L= \sum_{N}^{i=1} w_{m,i} \left( (1-e_m)e^{(-\alpha_m \ )} + e_me^{(\alpha_m \ )} \right) \]

对 \(\alpha_m\) 求偏导，令其为 \(0\)，则有：

\[\alpha_m = \frac{1}{2} log \frac{1-e_m}{e_m} \]



四、AdaBoost 回归算法

AdaBoost 回归算法。



五、AdaBoost 算法正则化

为防止 \(AdaBoost\) 过拟合，通常加入正则化项，这个正则化通常称为步长（\(learning\ rate\)）。定义为 \(\nu\)。

对于弱学习器的迭代，

\[f_m(x) = f_{m-1}(x) + \alpha_m G_m(x) \]

加上正则化项，

\[f_m(x) = f_{m-1}(x) + \nu \alpha_m G_m(x) \]

其中 \(0< \nu \leqslant 1\)。

对于同样的训练集，较小的 \(\nu\) 意味需要更多的弱学习器、迭代次数。通常我们用步长和迭代最大次数一起来决定算法的拟合效果。



六、AdaBoost 小结

\(AdaBoost\) 算法弱学习器通常是决策树和神经网络。对于决策树，\(AdaBoost\) 分类用 \(CART\) 分类树，\(AdaBoost\) 回归用 \(CART\) 回归树。

\(AdaBoost\) 优点：

  • 作为分类器时，分类精度高。
  • 可以使用各种回归分类模型构建弱学习器。
  • 不容易过拟合。

\(AdaBoost\) 缺点：

  • 对异常数据敏感，异常数据在迭代中会获得较高的权重。影响最终强学习器的预测准确性。


posted @ 2019-08-14 11:05  做梦当财神  阅读(493)  评论(1)  编辑  收藏  举报