支持向量机（二）线性支持向量机

支持向量机（一）线性可分支持向量机

支持向量机（二）线性支持向量机

支持向量机（三）非线性支持向量机与核函数

支持向量机（四）SMO算法

目录

• 一、线性支持向量机
• 二、对偶算法
  • 1.线性支持向量机对偶算法
• 三、支持向量

一、线性支持向量机

线性可分支持向量机对线性不可分数据不适用，因为这时的不等式约束不成立。需要修改硬间隔最大化为软间隔最大化。

线性不可分意味某些样本点 \((x_i,y_i)\) 不满足函数间隔 \(\ge1\) 的约束条件。可以对每个样本点 \((x_i,y_i)\) 引进一个松弛变量 \(\xi_i \ge 0\)，使函数间隔加上松弛变量 \(\ge 1\)。即：

\[y_i(\omega \cdot x_i+b) \ge 1-\xi_i \]

对每个松弛变量 \(\xi_i\)，支付一个代价 \(\xi_i\)。目标函数由原来的 \(\frac{1}{2}||\omega||^2\) 变为

\[\frac{1}{2} ||\omega||^2 + C \sum_{i=1}^{N} \xi_i \tag{1} \]

\(C>0\) 为惩罚参数，\(C\) 值越大表示对误分类惩罚越大。

最小化目标函数 \((1)\) 的两层含义：使 \(\frac{1}{2}||\omega||^2\) 尽量小即间隔尽量大，同时使误分类点的个数尽量小，\(C\) 是调和二者的系数。

线性支持向量机的优化问题作为原始问题：

\[\begin{align} \tag{2} \underset{\omega,b,\xi}{min} \ \ \ \ & \frac{1}{2}||\omega||^2+C\sum_{i=1}^{N} \xi_i \\ \tag{3} s.t. \ \ \ \ & y_i(\omega \cdot x_i+b) \ge 1-\xi_i, \ \ \ \ i=1,2,...,N \\ \tag{4} & \xi_i \ge 0, \ \ \ \ i=1,2,...,N \end{align} \]

原始问题 \((2)\thicksim (4)\) 是凸二次规划问题，因而 \((\omega,b,\xi)\) 的解是存在的。且 \(\omega\) 的解是唯一的，\(b\) 的解可能不唯一，而是存在一个区间内。

二、对偶算法

原始问题 \((2)\thicksim (4)\) 的对偶问题

\[\begin{align} \tag{5} \underset{\alpha}{min} \ \ \ \ & \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(x_{i} \cdot x_{j}\right)-\sum_{i=1}^{N} \alpha_{i} \\ \tag{6} s.t.\ \ \ \ & \sum_{i=1}^{N}\alpha_iy_i=0 \\ \tag{7} & 0 \le\alpha_i \le C,\ \ \ \ i=1,2,...,N \end{align} \]

原始最优化问题 \((2)\thicksim (4)\) 的拉格朗日函数是

\[L(\omega,b,\xi,\alpha,\mu)=\frac{1}{2}||\omega||^2+C\sum_{i=1}^{N}\xi_i-\sum_{i=1}^{N}\alpha_i(y_i(\omega \cdot x_i+b)-1+\xi_i)-\sum_{i=1}^{N}\mu_i\xi_i \tag{8} \]

其中，\(\alpha_i \ge 0\)，\(\mu_i \ge 0\)。

对偶问题是拉格朗日函数的极大极小问题。

首先 \(L(\omega,b,\xi,\alpha,\mu)\) 对 \(\omega,b,\xi\) 的极小，由

\[\bigtriangledown_\omega L(\omega,b,\xi,\alpha,\mu)=\omega-\sum_{i=1}^{N}\alpha_iy_ix_i=0 \]

\[\bigtriangledown_b L(\omega,b,\xi,\alpha,\mu)=-\sum_{i=1}^{N}\alpha_iy_i=0 \]

\[\bigtriangledown_{\xi_i} L(\omega,b,\xi,\alpha,\mu)=C-\alpha_i-\mu_i=0 \]

得

\[\omega=\sum_{i=1}^{N}\alpha_iy_ix_i \tag{9} \]

\[\sum_{i=1}^{N}\alpha_iy_i=0 \tag{10} \]

\[C-\alpha_i-\mu_i=0 \tag{11} \]

将式 \((9)\thicksim (11)\) 代入式 \((8)\)，得

\[\underset{\omega,b,\xi}{min} L(\omega,b,\xi,\alpha,\mu)=-\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i\alpha_jy_iy_j(x_i \cdot x_j)+\sum_{i=1}^{N}\alpha_i \]

再对 \(\underset{\omega,b,\xi}{min}\ L(\omega,b,\xi,\alpha,\mu)\) 求 \(\alpha\) 的极大，即得对偶问题：

\[\begin{align} \tag{12} \underset{\alpha}{max}\ \ \ \ & -\frac{1}{2} \sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i\alpha_jy_iy_j(x_i \cdot x_j)+\sum_{i=1}^{N}\alpha_i \\ \tag{13} s.t.\ \ \ \ & \sum_{i=1}^{N}\alpha_iy_i=0 \\ \tag{14} & C-\alpha_i-\mu_i=0 \\ \tag{15} & \alpha_i \ge 0 \\ \tag{16} & \mu_i \ge 0,\ \ \ \ i=1,2,...,N \\ \end{align} \]

将对偶最优化问题 \((12)\thicksim (16)\) 进行变换；利用等式约束 \((14)\) 消去 \(\mu_i\)，从而只留下变量 \(\alpha_i\)，并将约束 \((14)\thicksim (16)\) 写成

\[0 \le \alpha_i \le C \tag{17} \]

再将目标函数求极大转换为求极小，得到对偶问题 \((5)\thicksim (7)\)。通过求解对偶问题得到原始问题的解。

定理 ： 设 \(\alpha^*=(\alpha_1^*,\alpha_2^*,...,\alpha_N^*)^T\) 是对偶问题的解，若存在 \(\alpha^*\) 一个分量 \(\alpha_j^*\)，\(0<\alpha_j^*<C\)，按下式求原始问题的解 \(\omega^*\)、\(b^*\) ：

\[\begin{align} \tag{18} & \omega^*=\sum_{i=1}^{N}\alpha_i^*y_ix_i \\ \tag{19} & b^*=y_j-\sum_{i=1}^{N}\alpha_i^*y_i(x_i\cdot x_j) \end{align} \]

根据 \(KKT\) 条件可证明。

1.线性支持向量机对偶算法

输入：训练集 \(T={(x_1,y_1),(x_2,y_2),...,(x_N,y_N)}\)，其中 \(y_i\in(-1,1)\)

输出：分离超平面、分类决策树

① 选择惩罚参数 \(C>0\)，构造并求解凸二次规划问题

\[\begin{aligned} \underset{\alpha}{min}\ \ \ \ & \frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i\alpha_jy_iy_j(x_i\cdot x_j)-\sum_{i=1}^{N}\alpha_i \\ s.t.\ \ \ \ & \sum_{i=1}^{N}\alpha_iy_i=0 \\ & 0 \le \alpha_i \le C,\ \ \ \ i=1,2,...,N \end{aligned} \]

求得最优解 \(\alpha^*=(\alpha_1^*,\alpha_2^*,...,\alpha_N^*)^T\)。

② 计算 \(\omega^*\)、\(b^*\)。

\[\omega^*=\sum_{i=1}^{N}\alpha_i^*y_ix_i \]

选择 \(\alpha^*\) 一个分量 \(\alpha_j^*\)，\(0<\alpha_j^*<C\)，计算

\[b^*=y_j-\sum_{i=1}^{N}\alpha_i^*y_i(x_i\cdot x_j) \]

③ 求得分离超平面

\[\omega^*\cdot x+b^*=0 \]

分类决策函数：

\[f(x)=sign(\omega^*\cdot\ x+b^*) \]

理论上原始问题 \((2)\thicksim (3)\) 对 \(b\) 的解可能不唯一，然而在实际应用中，往往只会出现算法中的情况。

三、支持向量

在线性不可分的情况下，对偶问题 \((5)\thicksim (7)\) 的解 \(\alpha^*=(\alpha_1^*,\alpha_2^*,...,\alpha_N^*)^T\) 中对应 \(\alpha_i^*>0\) 的样本点 \((x_i,y_i)\) 的实例 \(x_i\) 称为支持向量（软间隔的支持向量）。

如下图，”○“ 表示正例，”ד 表示负例，实线表示分离超平面，虚线表示间隔边界，\(\frac{\xi_i}{||\omega||}\) 表示样本 \(x_i\) 到间隔边界的距离。

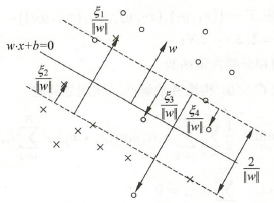
这时的支持向量比线性可分的情况复杂。支持向量 \(x_i\) 或者在间隔边界上，或者在间隔边界与分离超平面之间，或者在分离超平面误分一侧。

若 \(\alpha_i^*<C\)，则 \(\xi_i=0\)，支持向量 \(x_i\) 在间隔边界上；

若 \(\alpha_i^*=C\)，\(0<\xi_i<1\)，支持向量 \(x_i\) 在间隔边界与分离超平面之间；

若 \(\alpha_i^*=C\)，\(\xi_i=1\)，\(x_i\) 在分离超平面上；

若 \(\alpha_i^*=C\)，\(\xi_i>1\)，\(x_i\) 在分离超平面误分类一侧。