k 近邻法
\(k\) 近邻法(\(k-nearest\ neighbor,\ k-NN\))即可用于分类,也可用于回归。
\(KNN\) 做分类还是回归区别在预测时的决策方式。做分类时,用多数表决法;做回归时,用平均法。
sklearn-learn 中只使用了 蛮力实现(\(brute-force\))、\(kd\) 树(\(KDTree\))、球树(\(BallTree\))。
本文只讨论 \(k\) 近邻法在分类问题上的应用。
一、k 近邻法
\(k\) 近邻法思想:对于预测样本,在训练集中找到与该预测样本最邻近的 \(k\) 个,这 \(k\) 个样本的多数属于哪个类,就把该预测样本分为这个类。
\(k\) 近邻法中,当 \(k=1\)时,称为最近邻算法。
输入:训练集:\(T={(x_1,y_1), (x_2,y_2),..., (x_N,y_N)}\),\(i=1,2, \cdots, N\),
其中,\(x_i\) 为预测集样本, \(y_i\in \mathcal{Y}= \left\{c_1, c_2, \cdots, c_K \right\}\) 为样本的类别。
输出:样本 \(x_i\) 所属类别 \(y_i\)。
(1)根据给定的距离度量,在训练集 \(T\) 中找出与 \(x_i\) 最近邻的 \(k\) 个点,涵盖这 \(k\) 个点的 \(x_i\) 的邻域记作 \(N_k(x_i)\)。
(2)在 \(N_k(x_i)\) 中根据分类决策树规则(如多数表决)决定 \(x_i\) 的类别 \(y_i\)。
二、k 近邻模型
\(k\) 近邻模型三要素:距离度量、\(k\)值的选择、分类决策规则。
1. 距离度量
常用:曼哈顿距离、欧式距离、闵可夫斯基距离(曼哈顿距离是闵可夫斯基距离在 \(p=1\) 的特例,欧式距离是\(p =2\) 的特例)。
两个 \(n\) 维样本 \(x_i=(x_i^{(1)},x_i^{(2)},...,x_i^{(n)})^T\),\(x_j=(x_j^{(1)},x_j^{(2)},...,x_j^{(n)})^T\)。
曼哈顿距离:
欧式距离:
闵可夫斯基距离:
例 \(1\):3个点 \(x_1=(1,1)^T\),\(x_2=(5,1)^T\),\(x_3=(4,4)^T\),求 \(p\) 取不同值时,距离 \(x_1\) 的最近邻点。
解:因为 \(x_1\) 和 \(x_2\) 只有第一维的值不同, 所以 \(p\) 为任何值时, \(L_p(x_{1}, x_2)=4\) 。而 \(L_{1}\left(x_{1}, x_{3}\right)=6\),
\(L_{2}\left(x_{1}, x_{3}\right)=4.24\),\(L_{3}\left(x_{1}, x_{3}\right)=3.78\),\(L_{4}\left(x_{1}, x_{3}\right)=3.57\),
于是得到: \(p\) 等于 \(1\) 或 \(2\) 时, \(x_2\) 是 \(x_1\) 的最近邻点;\(p\) 大于等于 \(3\) 时, \(x_3\) 是 \(x_1\) 的最近 邻点。
2. k 值的选择
\(k\) 值较小,会用较小的领域的数据来训练,训练误差减小;预测时数据也较少,如果近邻的样本恰巧是噪声,预测出错,估计误差增大。
\(k\) 值较大,训练误差增大,估计误差减小。
极端情况 \(k=N\),无论测试集是什么,结果都是训练集中最多的类。
通常采用交叉验证法选取 \(k\) 值。
3. 分类规则
分类决策规则一般采用多数表决法。
三、k 近邻法蛮力实现
计算预测样本和训练集中所有样本的距离,然后得到最小的 \(k\) 个距离即可,接着多数表决,做出预测。
该方法简单,适合样本量少,样本特征少的情况。
四、kd 树
\(k\) 近邻法最简单的实现方法是线性扫描(即蛮力实现)。当训练集很大时,该方法不可行。为提高 \(k\) 近邻搜索效率,引入 \(kd\) 树。
\(kd\) 树就是 \(k\) 个特征维度的树。\(KNN\) 中 \(k\) 表示 \(k\) 个样本,\(kd\) 树中 \(k\) 表示特征维数。
\(kd\) 树算法包括3步:第一建树、第二搜索最近邻、第三预测。
1. 构造 kd 树
构造 \(kd\) 树方法:\(kd\) 树实质是二叉树,其切分点的选取与 \(CART\) 树类似,即选取使样本复杂度降低最多的特征。\(kd\) 树认为特征方差越大,则该特征的复杂度越大,优先对该特征进行切分,切分点是样本在该特征的中位数。重复该切分步骤,直到切分后子区域无样本则终止切分,终止时的样本为叶结点。
例 \(2\):训练集 \(T={(2,3)^T, (5,4)^T, (9,6)^T, (4,7)^T, (8,1)^T, (7,2)^T}\) ,构造 \(kd\) 树。
解:(1)找到切分特征。6个数据在第一个特征 \(x^{(1)}\)、第二个特征 \(x^{(2)}\) 的方差为 \(6.97\)、\(5.37\),所以用 \(x^{(1)}\) 构造 \(kd\) 树。
(2)确定切分点。6个数据在 \(x^{(1)}\) 的中位数是 7,所以切分点是\((7,2)\)。
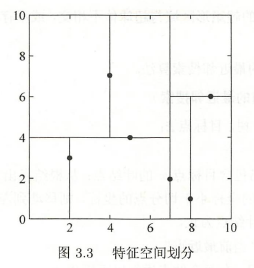
(3)确定左、右子区域。以平面 \(x^{(1)}=7\) 将空间划分为左、右两个子区域,\(\{(2,3),(5,4),(4,7)\}\)、\(\{(9,6),(8,1)\}\)。
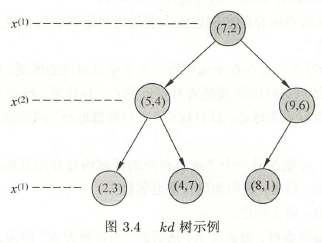
如此递归,直到两个子区域没有样本存在时停止。得到特征空间划分(图\(3.3\))和 \(kd\) 树(图\(3.4\))。
2. 搜索 kd 树
\(kd\) 树可以省去大部分数据点的搜索。
\(kd\) 树的最近邻搜索:
输入:\(kd\) 树,目标点 \(x\)。
输出:\(x\) 的最近邻。
(1)在 \(kd\) 树中找出包含目标点 \(x\) 的叶结点。
(2)以此叶结点为 “当前最近点”。
(3)递归地向上回退。在每个结点上进行以下操作:
- 以目标点为圆心,目标点到叶结点的距离为半径,得到一个超球体,如果该超球体内的样本点比叶结点距离目标更近,则以该样本点为 ”当前最近点“。
- 检查该叶结点的父结点的另一个子结点对应的区域是否有更近的点。具体地,检查另一子结点对应的超矩形体和超球体是否相交。如果相交,可能在超矩形体内存在距目标点更近的点,移动到另一个子结点。接着递归地进行最近邻搜搜。如果不想交,向上回退。
- 当回退到根节点时,搜索结束。最后的 “当前最近点” 为 \(x\) 的最近邻点。
如果样本点是随机分布的,\(kd\) 树搜索的计算复杂度是 \(O(logN)\),\(N\) 是训练集样本数。
\(kd\) 树适用于训练集样本数远大于空间维数的 \(k\) 近邻搜索。当空间维数接近训练集样本数时,效率几乎接近线性扫描。
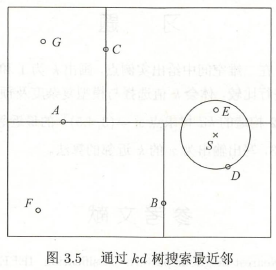
例 \(3\):如图 \(3.5\) 的 \(kd\) 树,根节点 \(A\),它的子结点为 \(B\)、\(C\)。树上总共 7 个样本点,目标点 \(S\),求 \(S\) 的最近邻。
解:在 \(k d\) 树中找到包含点 \(S\) 的叶结点 \(D\) , 以点 \(D\) 作为 近似最近邻。真正最近邻一定在以点 \(S\) 为中心通过点 \(D\)
的圆的内部。然后返回结点 \(D\) 的父结点 \(B\), 在结点 \(B\) 的另一子结点 \(F\) 的区域内搜索最近邻。结点 \(F\) 的区域与圆
不相交, 不可能有最近邻点。继续返回上一级父结点 \(A\), 在结点 \(A\) 的另一子结点 \(C\) 的 区域内搜索最近邻。结点 \(C\)
的区域与圆相交; 该区域在圆内的实例点有点 \(E\), 点 \(E\) 比 点 \(D\) 更近, 成为新的最近邻近似。最后得到点 \(E\) 是点 \(S\)
的最近邻。
3. kd 树预测
在 \(kd\) 树搜索最近邻时,选择第一个最近邻样本,把它置为已选。在第二轮选择中,忽略置为已选的样本,重新选择最近邻,这样跑 \(k\) 次,得到了 \(k\) 个最近邻,
如果是分类问题,根据多数表决法,预测为最多类别数的类别;
如果是回归问题,根据平均法,\(k\) 个最近邻样本的平均值作为回归预测值。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号