梯度下降法

 

求解机器学习算法的模型参数，即无约束优化问题，常用两种方法：梯度下降，最小二乘法。此外还有牛顿法和拟牛顿法。

 

1. 梯度

对多元函数参数求偏导，把求得的偏导写成向量形式。比如：f(x,y)对x，y求偏导，梯度就是(∂f/∂x, ∂f/∂y)^T。

 

2. 梯度下降法详解

梯度下降法有代数法和矩阵法两种表示形式。

 

2.1 代数法

1. 先决条件：确认模型的假设函数和损失函数

线性回归假设函数：

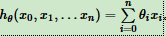
线性回归损失函数：

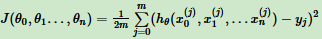
2. 参数初始化

初始化θ₀，θ₁...θ_n，算法终止距离ε，步长α。一般将所有的θ初始化为0，步长为1。

3. 算法过程

(1)、求当前位置损失函数的梯度。

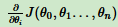
(2)、步长乘以梯度，得到当前位置下降距离。

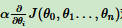
(3)、确定是否所有的θ_i，梯度下降的距离都小于ε，如果小于ε算法终止。当前所有θ_i(i = 1,2...n)为最终结果。否则进入步骤4.

(4)、更新所有的θ，更新完进入步骤1.

 

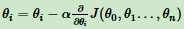
线性回归的例子：

损失函数：

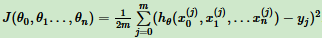
按步骤1对θ_i求偏导：

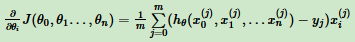
由于样本中没x₀，所以上式令所有为1。

步骤4中θ_i更新表达式为：

 

注意：第3节讲梯度下降法的变种，主要区别是对样本选取的方法不同，这里采用所有样本。

 

2.2 矩阵法

1. 先决条件：确认模型的假设函数和损失函数

线性回归假设函数：

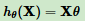
线性回归损失函数：

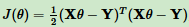
2. 参数初始化

初始化θ向量为默认值，算法终止距离ε，步长α。一般将所有的θ初始化为0，步长为1。

 

线性回归的例子：

对θ向量求偏导数：

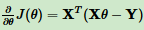
θ向量的更新表达式为：

 

 

2.3 梯度下降法调优

1. 步长选择。步长太大，迭代会过快，可能错过最优解；步长太小，迭代过慢。

2. 初始值选择。初始值不同，最小值可能不同，因为梯度下降法求得的是局部最小值。

3. 归一化。不同特征取值范围不一样，减少特征取值的影响，对数据归一化。

对每个特征x，求它的期望和标准差std(x)，然后转化为：

这样得到新期望为0，新方差为1。

 

3. 梯度下降法(BGD，SGD，MBGD)

3.1 批量梯度下降法(Batch Gradient Descent)

更新参数θ_i用所有样本进行更新。

 

3.2 随机梯度下降法(Stochastic Gradient Descent)

更新参数θ_i仅用一个样本j进行更新。

 

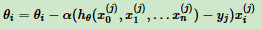
3.3 小批量梯度下降法（Mini-batch Gradient Descent）

小批量梯度下降法是批量梯度下降法和随机梯度下降法的折中， 对于m个样本，用x个样本来更新。

 

 

 来自：刘建平

hθ(x0,x1,...xn)=∑i=0nθixi