线性回归
1. 线性回归的模型函数和损失函数
对于m个样本，n维特征，
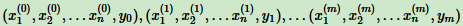
如果y是连续的，则是回归问题，否则是分类问题。
它的线性回归模型是：
θi (i = 1,2...n)是参数，xi (i = 1,2...n)是每个样本的n个特征。
这里增加一个特征 x0 = 1，得到 
矩阵形式的线性回归模型：hθ(x) = xΘ，其中hθ(x)为mx1的向量，θ为nx1的向量，x为mxn维的矩阵。
一般线性回归用均方误差作为损失函数。线性回归损失函数表达式：
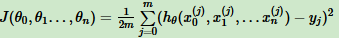
矩阵形式的线性回归损失函数：
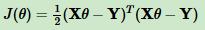
2. 线性回归算法
常用两种方法求线性回归损失函数的最小值：梯度下降法，最小二乘法。
梯度下降法，θ的跌代公式：
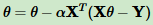
最小二乘法，θ的迭代公式：
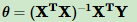
当然线性回归损失函数的求法还有牛顿法和拟牛顿法。
3.线性回归的推广：多项式回归
将多项式回归变为线性回归。
开始的线性模型：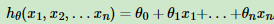
，如果这里有x的二次方，模型变为多项式回归。
比如：下面是二元（两个特征）多项式回归，
这样变化又回到线性回归，这是一个五元（五个特征）线性回归。
4. 线性回归的推广：广义线性回归
第三节线性推广对样本特征做了推广，这一节对特征 y 做推广。比如输出 Y 不满足和 X 的线性关系，但是 lnY 和 X 满足线性关系：
，这时可以对Y做变换。
5. 线性回归的正则化
为了防止模型过拟合，建立模型时需要正则化。一般有 L1 正则化和 L2正则化。
L1正则化的项用一个常数α 来调节损失函数的均方差和正则化的权重，表达式：
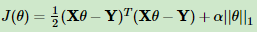
其中，α 为常数系数，需要进行调优。||θ||1 为L1范数（L1范数：向量各个元素绝对值之和。比如 向量A=[1，-1，3]， 那么A的L1范数为 |1|+|-1|+|3|）。
L1正则化可以使一些特征的系数变小，甚至使一些绝对值较小的系数直接变为0。增强模型泛化能力。
L2正则化表达式：
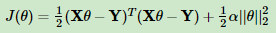
其中，α 为常数系数，需要进行调优。||θ||2 为L2范数（L2范数：向量各个元素平方和的1/2次方）。
L2正则化不抛弃任何一个特征，缩小了回归系数，使得模型相对稳定。但模型特征留有很多，解释性差。
L2正则化表达式求解一般用最小二乘法，下面是矩阵推导形式：
来自：刘建平
