最大熵模型
最大熵模型与逻辑回归类似，是对数线性分类模型。在损失函数优化过程中，使用和支持向量机类似的凸优化技术。对熵的使用，会想起决策树ID3和C4.5。
1. 最大熵模型的定义
将最大熵原理应用到分类得到最大熵模型。
用最大熵模型选择一个最好的分类模型。训练集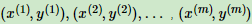
，其中x为n维特征向量，y为类别输出。
训练集总体联合分布 P(X, Y)的经验分布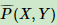
，和边缘分布P(X)的经验分布
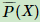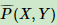。即为训练集中X，Y同时出现次数除以样本总数m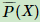，为训练集中X出现次数除以样本总数m。
用特征函数 f(x, y)描述 x 和 y 的关系。为：
可以认为训练集只要出现 (x(i), y(i))，其 f(x(i), y(i))=1。同一个训练集可以有多个约束特征函数。
特征函数 f(x, y)关于经验分布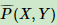期望值，用
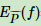表示为：
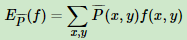
特征函数 f(x, y)关于条件分布 P(Y|X) 和经验分布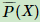的期望值，用
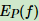表示为：
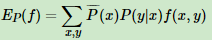
下式就是最大熵模型学习的约束条件，假如有M个特征函数 fi(x, y)(i = 1,2,3...M) 就有M个约束条件。可以理解为如果训练集里有 m 个样本，就有和这 m 个样本对应的 M 个约束条件。
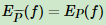
最大熵模型定义如下：
假设满足所有约束条件的模型集合为：
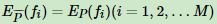
定义在条件概率分布 P(Y|X)上的条件熵为：
我们目的是求使 H(P) 最大时对应的 P(Y|X)，这里对 H(P) 加负号求极小值，目的是为了使 -H(P) 为凸函数，方便用凸优化求极值。
2. 最大熵模型损失函数优化
最大熵模型损失函数 -H(P)定义为：
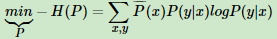
约束条件为：
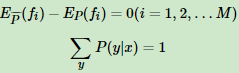
用拉格朗日函数将约束最优化转化为无约束最优化对偶问题，此时损失函数对应的拉格朗日函数 L(P, ω)定义为：
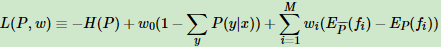
其中ωi(i=0,1,2,3...M)为拉格朗日乘子。这与支持向量机中用到的凸优化理论一样，用到了拉格朗日对偶。
凸优化原始问题：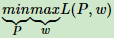
其对应的拉格朗日对偶问题为：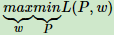
因此原始问题的解和对偶问题的解一致。可以通过求解对偶问题来求解原始问题。
求解对偶问题的第一步是求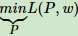
，这可以通过求导得到。得到的
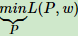是关于 ω 的函数。记为：
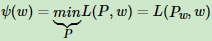
Ψ(ω)为对偶函数，将其解记为：
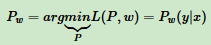
这样得到P(y|x)和ω的关系，从而把对偶函数Ψ(ω)里的所有P(y|x)替换成用ω表示，这样对偶函数Ψ(ω)就是全部用ω表示。接着对Ψ(ω)求极大化，得到极大化时对应ω向量的取值，带入P(y|x)和ω的关系式，从而也得到P(y|x)的最终结果。
3. 最大熵模型实例
例：假设随机变量 x 有5个取值{A,B,C,D,E}，其中P(A)+P(B) = 3/10，根据最大熵模型估计各个值的概率 P(A),P(B),P(C),P(D),P(E)。
解：用 y1,y2,y3,y4,y5 表示 A,B,C,D,E，于是最大熵模型的最优化问题是：
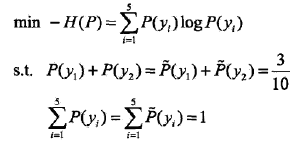
引入拉格朗日乘子 w0,w1，则拉格朗日函数为：
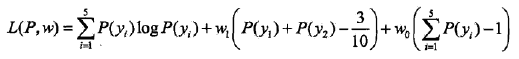
根据拉格朗日对偶性：
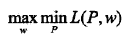
首先求解 L(P, w) 关于 P 的极小化问题，为此，固定 w0, w1,求偏导数：
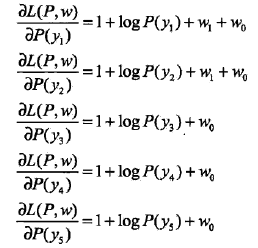
令各偏导数等于0，得：
于是
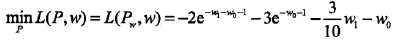
再求解 L(Pw, w) 关于 w 的极大化问题：
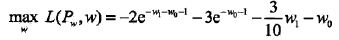
分别求 L(Pw, w) 对 w0, w1的偏导数并令其为0，得到
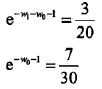
则所求概率分布为：
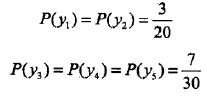
4. 最大熵模型小结
它的约束函数的数目会随样本量的增大而增大，导致样本量很大的时候，对偶函数优化求解的迭代过程非常慢，scikit-learn都没有最大熵模型对应的库。
