决策树-CART 回归树
分类回归树（\(classification\ and\ regression\ tree,\ CART\)）既可用于分类也可用于回归。
\(CART\)分类树、\(CART\) 回归树统称 \(CART\) 决策树。
\(CART\) 学习分三步：特征选择、决策树的生成、剪枝。
\(CART\) 决策树是二叉树。对 \(CART\) 回归树用均方误差最小化准则，\(CART\) 分类树用基尼系数最小化（\(Gini\ index\)）准则，进行特征选择，生成二叉树。
假设 \(X、Y\) 是输入、输出变量，\(Y\) 是连续的。给定训练集
生成回归树。
一颗回归树对应着输入空间（即特征空间）的一个划分以及在划分单元上的输出值。假设已将输入空间划分为 \(M\) 个单元 \(R_1,R_2,...,R_M\)，并且在每个单元 \(R_m\) 上有一个固定的输出值 \(c_m\)，于是回归树模型为
当输入空间划分确定时，可用平方误差 \(\sum_{x_i \in R_m} (y_i - f(x_i))^2\) 来表示回归树对训练数据的预测误差，用平方误差最小的准则求解每个单元上的最优输出值。易知，单元 \(R_m\) 上的 \(c_m\) 的最优值 \(\hat{c}_m\) 是 \(R_m\) 上的所有输入实例 \(x_i\) 对应的输出 \(y_i\) 的均值，即
CART回归树（或最小二乘回归树）生成算法：
基于均方误差最小化来进行模型求解的方法称为最小二乘法。
输入：训练集 \(D\)；
输出：回归树 \(f(x)\)。
在训练集所在的输入空间中，递归地将每个区域划分为两个子区域并决定每个子区域上的输出值，构建二叉树。
(1) 选择最优切分变量 \(j\) 、切分点 \(s\) 。
\[\tag{1} \underset{j,s}{min} \begin{bmatrix} \underset{c_1}{min} \ \sum_{x_i \in R_1(j,s)} (y_i - c_1)^2 + \underset{c_2}{min} \ \sum_{x_i \in R_2(j,s)} (y_i - c_2)^2 \end{bmatrix} \]遍历变量 \(j\)，对固定的切分变量 \(j\) 扫描切分点 \(s\)，选择使式 \((1)\) 达到最小值的 \((j,s)\)。
(2) 用选定的 \((j,s)\) 划分区域并决定响应的输出值：
\[R_1(j,s) = \{x|x^{(j)} \leqslant s\},\ \ \ \ R_2(j,s) = \{x|x^{(j)}>s\} \\ \hat{c}_m = \frac{1}{N_m} \ \sum_{x_i \in R_m(j,s)} y_i,\ \ \ \ x \in R_m,\ \ \ \ m=1,2 \]\(N_m\) 表示叶子结点的样本个数。
(3) 继续对两个子区域调用步骤 \((1),(2)\)，直到满足停止条件。
(4) 将输入空间划分为 \(M\) 个区域 \(R_1,R_2,...,R_M\)，生成回归树：
\[f(x) = \sum_{m=1}^{M} \hat{c}_mI(c \in R_m) \]
即：
- 考虑数据集 \(D\) 上的所有特征 \(j\)，遍历每一个特征下所有可能的取值即切分点 \(s\)，将数据集分为两部分 \(R_1\)、\(R_2\)。
- 分别计算两个子集的均方误差和，选择最小的均方误差对应的切分特征、切分点，生成两个子区域。
- 对子区域递归调用步骤 \(1\)、\(2\)，直到满足停止条件。
例 \(1\)：数据集 \(D\)。
选择切分特征 \(0\)，切分点 \(3\)，将数据分为两部分。
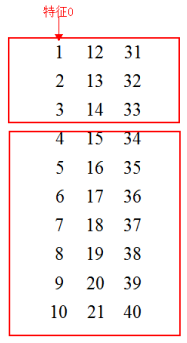
同样，选择切分特征 \(1\)，切分点 \(20\)，将数据分为两部分。
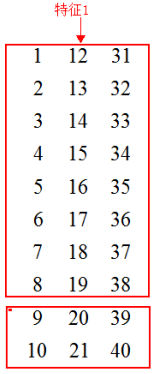
以上就是切分特征、切分点的选择。
