K-Means 聚类算法

 

　　K-Means算法是无监督聚类算法，它有很多变体。包括初始化优化K-Means++，距离计算优化elkan K-Means算法和大样本优化Mini Batch K-Means算法。

 

1. K-Means原理

　　K-Means算法思想：按照样本之间距离大小，将样本划分为K个簇。让簇内点尽量连在一起，簇间的距离尽量的大。

　　(KNN算法思想：如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多属于一个类别，则该样本也属于这个类别。)

　　用数据表达式表示，簇划分为（C₁，C₂，...C_k），目标是最小化平方误差E：

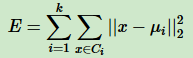
　　其中μ_i是簇C_i的均值向量，有时也是质心，表达式：

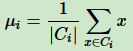
　　直接求上式最小值，不容易，是NP难题，只能采用启发式的迭代算法。

　　K-Means采用的启发式方式很简单，用下图可形象描述：

　　

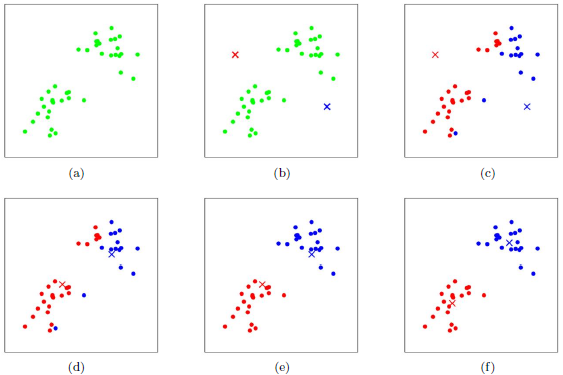
　　上图a初始数据集，假设 k=2。图b中，随机选择2个类别质心，即图中的红色质心和蓝色质心，然后求样本中所有点到这两个质心的距离，并标记每个样本的类别为距离最小的质心的类别，如图c，这样得到第一轮迭代后的类别。此时，对当前标记的红色和蓝色点分别求新的质心，如图d，图e和图f重复图c和图d的过程。即将所有点的类别标记为距离最近的质心的类别并求新的质心。

 

2. 传统K-Means算法流程

注意事项：

(1)、k 值的选择，一般根据经验选择一个合适 k 值，没有经验，通过交叉验证选择。

(2)、k 个质心的选择，质心的初始位置对最后的聚类结果和运行有很大影响。

算法流程：

输入：样本集D = {x₁,x₂,...x_m}，聚类的簇数k，最大迭代次数N

输出：簇划分C = {C₁,C₂,...C_k}

(1)、从数据集D中随机选择K个样本作为初始的k个质心向量：{μ₁，μ₂，...μ_k}

(2)、对n = 1,2,...N

　　a、将簇划分C初始化为C_t = Ø (t = 1,2...k)

　　b、对于 i = 1,2,...m，计算样本 x_i 和各个质心向量 μ_j (j = 1,2...k) 的距离：，将 x_i 标记为 d_ij 最小所对应的类别 λ_i 。此时更新。

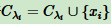　　c、对于 j = 1,2,...k，对 C_j 中所有样本点重新计算新的质心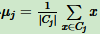

　　e、如果所有 k 个质心向量没发生变化，转到步骤3.

(3)、输出簇划分C = {C₁,C₂,...C_k}

 

3. K-Means初始化优化K-Means++

　　K-Means++是对K-Means随机初始化质心方法的优化。

　　策略如下：

　　a、从数据中随机选择一个点作为第一个聚类中心 μ₁

　　b、对数据集中的每个点 x_i ，计算它与已选择聚类中心中最近聚类中心的距离

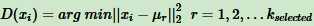
　　c、选择一个新的数据点作为新的聚类中心，选择的原则为：D(x)较大的点被选择作为聚类中心的概率大

　　d、重复 b 和 c 直到选出 k 个聚类质心

　　e、利用这 k 个质心作为初始化质心去运行标准的 K-Means算法

 

4. K-Means距离计算优化elkan K-Means

　　传统的 K-Means 算法，每轮迭代时，计算所有样本点到所有质心的距离，比较耗时。elkan K-Means 目标是减少不必要的距离计算。

　　elkan K-Means 利用两边之和大于第三边，以及两边之差小于第三边来减少距离计算。

　　第一种规律是对于每一个样本点 x 和 两个质心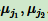。如果预先计算出这两个质心之间的距离 D(j₁, j₂) ，发现 2D(x, j₁) ≤ D(j₁, j₂)，则 D(x, j₁) ≤ D(x, j₂)。此时不需要计算 D(x, j₂) 。

　　第二种规律是对于每一个样本点 x 和两个质心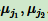。可以得到 D(x, j₂) ≥ max{0, D(x, j₁) - D(j₁, j₂)}。这个从三角形性质很容易得到。

　　利用上面两个规律，elkan K-Means 比传统的 K-Means 迭代速度有很大提高。但如果样本特征稀疏，有缺失值的话，这个方法不适用，因为某些距离无法计算，不能使用该算法。

 

5. 大样本优化 Mini Batch K-Means

　　如果样本量非常大，10万以上，特征100万以上，K-Means 非常耗时，就算 elkan K-Means 优化也很耗时。此时用 Mini Batch K-Means。

　　顾名思义，Mini Batch，就是用样本集中的一部分做传统的 K-Means，代价就是聚类的精度有一些降低。

　　在 Mini Batch K-Means ，选择合适的 batch size 来做 K-Means 聚类。一般通过无放回的随机采样得到。

　　为了增加算法的准确性，一般会多跑几次 Mini Batch K-Means 算法，用不同的随机采样集来得到聚类簇，选择其中最优的聚类簇。

 

6. K-Means与KNN

　　不同点：

1. K-Means是无监督学习的聚类算法，没有样本输出；而KNN是监督学习的分类算法（也可以用于聚类），有对应的类别输出。
2. KNN基本不需要训练，对测试集里面的点，只需要找到在训练集中最近的k个点，用这最近的k个点的类别来决定测试点的类别。而K-Means则有明显的训练过程，找到k个类别的最佳质心，从而决定样本的簇类别。
3. KNN数据集有Label，K-Means数据无Label。

　　相似点：

　　两个算法都包含一个过程，即找出和某一个点最近的点。两者都利用了最近邻(nearest neighbors)的思想。

 

7. K-Means小结

　　K-Means的主要优点有：

　　1）原理比较简单，实现也是很容易，收敛速度快。

　　2）聚类效果较优。

　　3）算法的可解释度比较强。

　　4）主要需要调参仅仅是簇数k。

　　K-Means的主要缺点有：

　　1）K值的选取不好把握

　　2）对于不是凸的数据集比较难收敛

　　3）如果各隐含类别的数据不平衡，比如各隐含类别的数据量严重失衡，或者各隐含类别的方差不同，则聚类效果不佳。

　　4） 采用迭代方法，得到的结果只是局部最优。

　　5） 对噪音和异常点比较的敏感

 

 

 来自：刘建平