逻辑回归

目录

• 一、逻辑斯谛分布
• 二、二元逻辑回归模型
• 三、线性回归到逻辑回归
• 四、二元逻辑回归损失函数
• 五、二元逻辑回归损失函数优化
• 六、二元逻辑回归损失函数正则化

逻辑回归（$Logistic\ \ regression$​​​）是分类方法。可以处理二元分类和多元分类。

一、逻辑斯谛分布

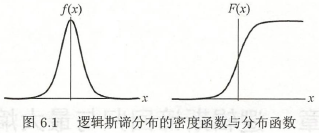
逻辑斯谛分布的密度函数 $f(x)$ 和分布函数 $F(x)$​ 如图。分布函数属于逻辑斯谛函数，曲线以点 $\left(\mu ,\frac{1}{2}\right)$ 中心对称。

二、二元逻辑回归模型

二元逻辑回归模型是如下条件概率分布：

$$P(Y=1|x)=\frac{e^{(\theta \ \bullet \ x+b)}}{1+e^{(\theta \ \bullet \ x+b)}} \tag{1}$$

$$P(Y=0|x)=\frac{1}{1+e^{(\theta \ \bullet \ x+b)}} \tag{2}$$

$x \in \pmb{R^n}$ （$n$ 维），$Y\in\{0,1\}$，$\theta \in \pmb{R^n}$ ，$\theta$ 称为权值向量，$b$​ 称为偏置。

对给定的样本 $x$​，带入式 $(1)$​、$(2)$​ 求得两个概率值​。比较概率值的大小，将 $x$​ 分为概率大的那一类。

为了方便，将 $\theta$​ 和 $x$​ 加以扩充，即 $\theta=(\theta^{(1)},\theta^{(2)},...,\theta^{(n)},b)^T$​，$x=(x^{(1)},x^{(2)},...,x^{(n)},1)^T$​

二元逻辑回归模型如下：

$$P(Y=1|x)=\frac{e^{(\theta \ \bullet \ x)}}{1+e^{(\theta \ \bullet \ x)}} \tag{3}$$

$$P(Y=0|x)=\frac{1}{1+e^{(\theta \ \bullet \ x)}} \tag{4}$$

一个事件的几率指发生的概率与不发生的概率比值。

事件的对数几率（$logit$ 函数）是:

$$logit(p)=log \frac{p}{1-p}$$

由式 $(3)$、$(4)$得

$$log \frac{P(Y=1|x)}{1-P(Y=1|x)}=\theta \ \bullet \ x$$

即输出 $Y=1$ 的对数几率是 由输入 $x$​ 的线性函数表示的模型，即逻辑回归模型。

则

$$P(Y=1|x)=\frac{1}{1+e^{(-\theta \ \bullet \ x)}}$$

三、线性回归到逻辑回归

线性回归模型 $y$​​​​​ 和 $x$​​​​​​ 之间的线性关系系数 $\theta$​​​​​，​满足 $y=\theta \ \bullet \ x$​。因为此时 $y$ 是连续的，所以是回归模型。

从线性回归到逻辑回归，需要 $y$ 是离散，对 $y$ 做转换，变为 $g(y)$。如果 $g(y)$ 结果是两种，就是二元分类模型。

$g$ 一般取 $sigmoid$ 函数：

$$g(y)=\frac{1}{1+e^{-y}}$$

取 $sigmoid$ 函数的原因有两个：

• 当 $y$ 趋于正无穷，$g(y)$ 趋于1，当 $y$​ 趋于负无穷，$g(y)$ 趋于0。
• $g(y)$ 容易求导。$g'(y)=g(y)(1-g(y))$

令 $g(y)$​ 中的 $y$​ 为：$y=\theta \ \bullet \ x$​​，得到二元逻辑回归的一般形式：

$$h_\theta(x)=\frac{1}{1+e^{(-\theta \ \bullet \ x)}}$$

四、二元逻辑回归损失函数

线性回归 $Y$​​ 是连续的，用均方误差定义损失函数。但逻辑回归不连续，用极大似然估计法求损失函数。

设：

$$\begin{aligned} & P(Y=1|x)=h_\theta(x) \\ & P(Y=0|x)=1-h_\theta(x) \end{aligned}$$

两个式子写成一个式子：

$$P(Y|x)=h_\theta(x)^y(1-h_\theta(x))^{(1-y)}$$

似然函数为：

$$L(\theta)=\prod_{i=1}^{m}(h_\theta(x^{(i)}))^{y{(i)}}(1-h_\theta(x^{(i)}))^{1-y^{(i)}}$$

$m$ 为样本个数。

对数似然函数取反即为损失函数：

$$\begin{aligned} J(\theta)=-lnL(\theta) &= -\sum_{i=1}^m (y^{(i)}log(h_\theta(x^{(i)}) + (1-y^{(i)})log(1-h_\theta(x^{(i)}))) \\ &= -\sum_{i=1}^m y^{(i)}log(h_\theta(x^{(i)}) - \sum_{i=1}^m (1-y^{(i)})log(1-h_\theta(x^{(i)})) \end{aligned}$$

损失函数矩阵形式：

$$J(\theta)=-Y^Tlogh_\theta(X)-(E-Y)^Tlog(E-h_\theta(X))$$

其中 $E$ 为全 $1$ 向量。

五、二元逻辑回归损失函数优化

损失函数最小话，常见的有梯度下降法、坐标轴下降法、等牛顿法。

六、二元逻辑回归损失函数正则化

逻辑回归有时也有过拟合问题，需要正则化。

$L1$ 正则化：

$$J(\theta)=-Y^Tlogh_\theta(X)-(E-Y)^Tlog(E-h_\theta(X))+\alpha\|\theta\|_1$$

其中 $\|\theta\|_1$为 $\theta$ 的 $L1$ 范数。

$L1$​ 正则化损失函数优化方法常用：坐标轴下降法、最小角回归法。

$L2$​ 正则化：

$$J(\theta)=-Y^Tlogh_\theta(X)-(E-Y)^Tlog(E-h_\theta(X))+\frac{1}{2}\alpha\|\theta\|_2^2$$

其中 $\|\theta\|_2$​​为 $\theta$​​ 的 $L2$​​ 范数。

$L1$ 正则化损失函数优化方法与普通逻辑回归类似。

逻辑回归尤其二元逻辑回归，虽然没支持向量机（$SVM$​）占主流，但训练速度比 $SVM$ 快很多。