决策树-ID3、C4.5
决策树可用于分类(\(ID3、C4.5、CART\) ),也可用于回归(\(CART\)),同时适合集成学习比如随机森林。
决策树学习分3步:特征选择、决策树的生成、剪枝。
一、分类决策树模型与学习
1.决策树模型
分类决策树模型由结点和有向边组成。
结点分两部分:内部节点、叶节点。内部结点表示一个特征或属性,叶节点表示一个类。
2.决策树学习
假设训练集
其中,\(x_i=(x_i^{(1)},x_i^{(2)},...,x_i^{(n)})\) 为输入实例(特征向量),\(n\) 为特征个数,\(y_i\in \{1,2,...,K\}\) 为类标记,\(N\) 为样本容量。
学习目标:构建决策树模型,能对实例进行正确分类。
学习本质:从训练集中估计条件概率模型。
决策树学习用损失函数表示这一目标,决策树损失函数是正则化的极大似然函数。
决策树常用算法:\(ID3\)、\(C4.5\)、\(CART\) ,结合这些算法分别叙述特征选择、决策树的生成、剪枝。
二、特征选择
特征选择的准则通常是:信息增益、信息增益比、基尼系数。
1.信息增益
熵:度量随机变量的不确定性,越不确定,熵就越大。随机变量 \(X\) 的熵定义为
其中 \(n\) 代表 \(X\) 的 \(n\) 种不同的离散取值。而 \(p_i\) 代表 \(X\) 取值为 \(i\) 的概率,通常 \(log\) 是以 \(2\) 或 \(e\) 为底的对数。
由定义可知,熵只依赖 \(X\) 的分布,与 \(X\) 的取值无关。所以也可将随机变量 \(X\) 的熵定义为
例 \(1\):当随机变量只有两个取值 \(1,0\) 时。
解:如果取值概率各为 \(\frac{1}{2}\) 时, \(X\) 的熵最大,\(X\) 具有最大的不确定性为:
\(H(X) = -\sum_{i=1}^{2} p_i logp_i = -(\frac{1}{2} log \frac{1}{2} + \frac{1}{2} log \frac{1}{2}) = log2\)。
如果一个值的概率大于 \(\frac{1}{2}\),另一个值的概率小于 \(\frac{1}{2}\),则不确定性减小,对应的熵减小。比如一个概率 \(\frac{1}{3}\),一个概率 \(\frac{2}{3}\),则熵为:
\(H(X) = -\sum_{i=1}^{2} p_i logp_i = -(\frac{1}{3} log \frac{1}{3} + \frac{2}{3} log \frac{2}{3}) = log3-\frac{2}{3}log2 < log2\)。
熵 \(H(p)\) 随概率 \(p\) 变换的曲线(以 \(2\) 为底)。
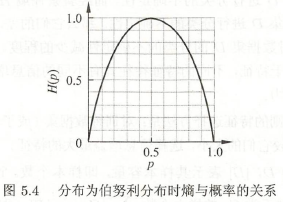
联合熵:已知熵容易推广到联合熵,这里给出两个变量 \(X\) 和 \(Y\) 的联合熵:
条件熵:已知联合熵容易推广到条件熵,条件熵表示已知 \(Y\) 的条件下 \(X\) 的不确定性。
信息增益:也称互信息,表示已知 \(Y\) 的条件下 \(X\) 不确定性减少的程度。
信息增益算法:
训练集为 \(D\),\(|D|\) 表示样本容量,即样本个数。设有 \(K\) 个类 \(C_k\),\(k=1,2,...,K\),\(|C_k|\) 为类 \(C_k\) 的样本个数,\(\sum_{k=1}^{K} |C_k| = |D|\)。
设特征 \(A\) 有 \(n\) 个不同的取值 \(\{a_1,a_2,...a_n\}\),根据特征 \(A\) 的取值将 \(D\) 划分为 \(n\) 个子集 \(D_1,D_2,...,D_n\),\(|D_i|\) 为 \(D_i\) 的样本个数,\(\sum_{i=1}^{n} |D_i| = |D|\)。记子集 \(D_i\) 中输入类 \(C_k\) 的样本集合为 \(D_{ik}\),即 \(D_{ik} = D_i \cap C_k\),\(|D_{ik}|\) 为 \(D_{ik}\) 的样本个数。
输入:训练集 \(D\) 和 特征 \(A\);
输出:特征 \(A\) 对训练集 \(D\) 的信息增益 \(g(D, A)\)。
① 计算数据集 \(D\) 的熵 \(H(D)\)。(也称经验熵)
\[H(D) = -\sum_{k=1}^{K} \frac{|C_k|}{|D|} log_2 \frac{|C_k|}{|D|} \]② 计算特征 \(A\) 对数据集 \(D\) 的条件熵 \(H(D|A)\)。(也称经验条件熵)
\[H(D|A) = \sum_{i=1}^{n} \frac{|D_i|}{|D|} H(D_i) = -\sum_{i=1}^{n} \frac{|D_i|}{|D|} \sum_{k=1}^{K} \frac{|D_{ik}|}{|D_i|} log_2 \frac{|D_{ik}|}{|D_i|} \]③ 计算信息增益。
\[g(D,A) = H(D)-H(D|A) \]
例 \(2\): 下表由15个样本组成的贷款申请训练数据。包括4个特征:
年龄:青年、中年、老年;
工作:是、否;
房子:是、否;
信贷:非常好、好、一般。
| ID | 年龄 | 有工作 | 有自己的房子 | 信贷情况 | 类别 |
|---|---|---|---|---|---|
| 1 | 青年 | 否 | 否 | 一般 | 否 |
| 2 | 青年 | 否 | 否 | 好 | 否 |
| 3 | 青年 | 是 | 否 | 好 | 是 |
| 4 | 青年 | 是 | 是 | 一般 | 是 |
| 5 | 青年 | 否 | 否 | 一般 | 否 |
| 6 | 中年 | 否 | 否 | 一般 | 否 |
| 7 | 中年 | 否 | 否 | 好 | 否 |
| 8 | 中年 | 是 | 是 | 好 | 是 |
| 9 | 中年 | 否 | 是 | 非常好 | 是 |
| 10 | 中年 | 否 | 是 | 非常好 | 是 |
| 11 | 老年 | 否 | 是 | 非常好 | 是 |
| 12 | 老年 | 否 | 是 | 好 | 是 |
| 13 | 老年 | 是 | 否 | 好 | 是 |
| 14 | 老年 | 是 | 否 | 非常好 | 是 |
| 15 | 老年 | 否 | 否 | 一般 | 否 |
解:计算熵 \(H(D)\)。
然后计算各特征对数据集 \(D\) 的信息增益。分别以 \(A_1,A_2,A_3,A_4\) 表示年龄、有工作、有房子、信贷 \(4\) 个特征。
①
这里 \(D_1,D_2,D_3\) 分别是 \(D\) 中 \(A_1\) (年龄)取值为青年、中年、老年的样本子集。
②
③
④
由于 \(A_3\) 的信息增益最大,所以选择 \(A_3\) 为最优特征。
2.信息增益比
以信息增益划分训练集的特征,容易偏向选择取值较多的特征。使用信息增益比可以对矫正这个问题。
信息增益比:
信息增益比 \(g_R(D,A)\) 为信息增益 \(g(D,A)\) 与训练集 \(D\) 关于特征 \(A\) 的值的熵 \(H_A(D)\) 之比。
其中,\(H_A(D)=-\sum_{i=1}^{n} \frac{|D_i|}{|D|} log_2 \frac{|D_i|}{|D|}\),\(n\) 为特征 \(A\) 的取值个数。
三、决策树的生成
1. ID3 算法
算法核心:用信息增益最大的特征作为结点的特征,由该特征的不同取值建立子结点,递归地构建决策树,直到信息增益都很小或没有特征可以选择为止。
输入:训练集 \(D\),特征集 \(A\) 阈值 \(\varepsilon\);
输出:决策树 \(T\)。
① 若 \(D\) 中所有实例属于同一类 \(C_k\),则 \(T\) 为单结点树,并将类 \(C_k\) 作为该结点的类标记,返回 \(T\);
② 若 \(A=\phi\),则 \(T\) 为单节点树,并将 \(D\) 中实例数最大的类 \(C_k\) 作为该结点的类标记,返回 \(T\);
③ 否则,按信息增益算法计算 \(A\) 中各特征对 \(D\) 的信息增益,选择信息增益最大的特征 \(A_g\);
④ 如果 \(A_g\) 的信息增益小于阈值 \(\varepsilon\),则置 \(T\) 为单结点树,并将 \(D\) 中实例数最大的类 \(C_k\) 作为该结点的类标记,返回 \(T\);
⑤ 否则,对 \(A_g\) 的每一可能值 \(a_i\),依 \(A_g=a_i\) 将 \(D\) 分割为若干非空子集 \(D_i\),将 \(D_i\) 中实例数最大的类作为标记,构建子结点,由节点及子结点构成树 \(T\),返回 \(T\);
⑥ 对第 \(i\) 个子结点,以 \(D_i\) 为训练集,以 \(A-\{A_g\}\) 为特征集,递归地调用步骤 \((1) \thicksim (5)\),得到子树 \(T_i\),返回 \(T_i\)。
例 \(3\):对例 \(2\) 中的数据,利用 \(ID3\) 算法建立决策树。
解:由于特征 \(A_3\)(有自己的房子)信息增益最大,所以 \(A_3\) 作为根节点,
由于 \(A_3\) 有两个取值,所以将数据集 \(D\) 分为 \(D_1\)(是)和 \(D_2\)(否)。 \(D_1\) 只有同一类样本点,即允许贷款,所以是叶节点。
对 \(D_2\) 从 \(A_1、A_2、A_4\) 中选择新的特征。计算各特征信息增益:
选择特征 \(A_2\)(有工作)作为结点的特征。
由于 \(A_2\) 两个取值,所以数据集 \(D_2\) 划分为两个子结点:一个对应“是”(有工作)的子结点,包含 \(3\) 个样本,属于同一类,即允许贷款,所以是叶结点;另一个对应“否”(无工作)的子结点,包含 \(6\) 个样本,也属于同一类,即不允许贷款,所以也是叶结点。
最终生成的决策树:

2. C4.5 算法
\(C4.5\) 对 \(ID3\) 进行改进,用信息增益比来选择特征。
输入:训练集 \(D\),特征集 \(A\) 阈值 \(\varepsilon\);
输出:决策树 \(T\)。
① 若 \(D\) 中所有实例属于同一类 \(C_k\),则 \(T\) 为单结点树,并将类 \(C_k\) 作为该结点的类标记,返回 \(T\);
② 若 \(A=\phi\),则 \(T\) 为单节点树,并将 \(D\) 中实例数最大的类 \(C_k\) 作为该结点的类标记,返回 \(T\);
③ 否则,按信息增益算法计算 \(A\) 中各特征对 \(D\) 的信息增益,选择信息增益最大的特征 \(A_g\);
④ 如果 \(A_g\) 的信息增益比小于阈值 \(\varepsilon\),则置 \(T\) 为单结点树,并将 \(D\) 中实例数最大的类 \(C_k\) 作为该结点的类标记,返回 \(T\);
⑤ 否则,对 \(A_g\) 的每一可能值 \(a_i\),依 \(A_g=a_i\) 将 \(D\) 分割为若干非空子集 \(D_i\),将 \(D_i\) 中实例数最大的类作为标记,构建子结点,由节点及子结点构成树 \(T\),返回 \(T\);
⑥ 对第 \(i\) 个子结点,以 \(D_i\) 为训练集,以 \(A-\{A_g\}\) 为特征集,递归地调用步骤 \((1) \thicksim (5)\),得到子树 \(T_i\),返回 \(T_i\)。
3. ID3 的不足
① \(ID3\) 不能处理连续值,比如长度、密度都是连续的,无法在 \(ID3\) 运用。
② \(ID3\) 用信息增益选择特征容易偏向取值较多的特征。在相同条件下,取值较多的特征比取值较少的特征信息增益大。比如一个变量 \(2\) 个值,各位 \(\frac{1}{2}\),另一个变量 \(3\) 个值,各为 \(\frac{1}{3}\),其实它们都是完全不确定的变量,但取 \(3\) 个值比取 \(2\) 个值的信息增益大。
③ \(ID3\) 不能处理缺失值。
④ 没考虑过拟合问题。
4. C4.5 对 ID3 的改进
1.信息增益比
\(C4.5\) 对 \(ID3\) 进行改进,用信息增益比来选择特征。
2.连续值处理
连续特征的取值数目是无限的,不能直接根据连续特征的取值来对结点进行划分,需连续特征离散化。最简单的二分法。
① 将 \(n\) 个连续值从小到大排列。
给定样本集 \(D\) 和连续特征 \(a\),特征 \(a\) 在 \(D\) 上有 \(n\) 个不同的取值,经从小到大排列,记为 \(\{a^1,a^2,...,a^n\}\)。
② 取相邻两样本值的中位点(平均值),得到 \(n-1\) 个划分点。
特征 \(a\) 的第 \(i\) 个划分点记为 \(T_a = \frac{a^i+a^{i+1}}{2}\),然后,就可像离散特征值一样来考察这些划分点。
③ 用信息增益最大的点作为最优的划分点进行样本集的划分。
④ 用信息增益比来选择特征,构建决策树。
注意:
- 与离散特征不同,若当前结点为连续特征,该特征还可作为后代结点的划分特征。
- 选择划分点用信息增益,选择特征用信息增益比。
例 \(4\):西瓜数据集上的两个连续特征 “密度”、"含糖率"。
| 编号 | 密度 | 含糖率 | 好瓜 |
|---|---|---|---|
| 1 | 0.697 | 0.460 | 是 |
| 2 | 0.774 | 0.376 | 是 |
| 3 | 0.634 | 0.264 | 是 |
| 4 | 0.608 | 0.318 | 是 |
| 5 | 0.556 | 0.215 | 是 |
| 6 | 0.403 | 0.237 | 是 |
| 7 | 0.481 | 0.149 | 是 |
| 8 | 0.437 | 0.211 | 是 |
| 9 | 0.666 | 0.091 | 否 |
| 10 | 0.243 | 0.267 | 否 |
| 11 | 0.245 | 0.057 | 否 |
| 12 | 0.343 | 0.099 | 否 |
| 13 | 0.639 | 0.161 | 否 |
| 14 | 0.657 | 0.198 | 否 |
| 15 | 0.360 | 0.370 | 否 |
| 16 | 0.593 | 0.042 | 否 |
| 17 | 0.719 | 0.103 | 否 |
① 对连续特征 “密度”,将 \(17\) 个样本值从小到大排列。
② 取相邻两样本值的中位点,得到 \(16\) 个划分点。
③ 选取信息增益最大的点作为最优的划分点进行样本集的划分。
所以特征 “密度” 的信息增益为 \(0.262\),对应划分点 \(0.381\)。密度小于 \(0.381\) 的是坏瓜,大于 \(0.381\) 是好瓜。
特征 “含糖率” 的信息增益为 \(0.349\),对应划分点 \(0.216\)。
④ 用信息增益比来选择特征,构建决策树。
3.缺失值处理
主要解决两个问题:
① 如何在数据缺失的情况下进行划分特征选择。
② 给定划分特征,若样本在该特征上的值缺失,如何对样本进行划分。
给定训练集 \(D\) 和特征 \(a\),令 \(\tilde{D}\) 表示 \(D\) 中在特征 \(a\) 上没有缺失值的样本子集。
对问题 ①:
我们可根据 \(\tilde{D}\) 来进行特征选择。假定特征 \(a\) 有 \(V\) 个可取值 \(\{a^1,a^2,...,a^V\}\),
令 \(\tilde{D}^v\) 表示 \(\tilde{D}\) 中在特征 \(a\) 上取值为 \(a^v\) 的样本子集,
\(\tilde{D}_k\) 表示 \(\tilde{D}\) 中第 \(k\) 类\((k=1,2,...,|\mathcal{Y}|)\)的样本子集,
假定为每个样本 \(x\) 赋予一个权重 \(\omega_x\),并定义
对特征 \(a\),\(\rho\) 表示无缺失值样本所占的比例,\(\tilde{p}_k\) 表示无缺失值样本中第 \(k\) 类所占的比例,\(\tilde{r}_v\) 表示无缺失值样本中在属性 \(a\) 上取值 \(a^v\) 的样本所占的比例。显然,\(\sum_{k=1}^{\mathcal{|Y|}} \tilde{p}_k = 1\),\(\sum_{v=1}^{V} \tilde{r}_v = 1\)。
此时信息增益:
对问题 ②:
若样本 \(x\) 的划分特征已知,则将 \(x\) 划入该特征对应的子结点,且样本权值在子结点中保持为 \(\omega_x\)。
若样本 \(x\) 的划分特征未知,则将 \(x\) 划入所有子结点,且样本权值在各个子结点中调整为 \(\tilde{r}_v \cdot \omega_x\),这就让同一样本以不同的概率划入到不同的子结点中。
例 \(5\):西瓜数据集出现缺失值,仅有编号 \(\{4,7,14,16\}\) 完整。
| 编号 | 色泽 | 根蒂 | 敲声 | 纹理 | 脐部 | 触感 | 好瓜 |
|---|---|---|---|---|---|---|---|
| 1 | — | 蜷缩 | 浊响 | 清晰 | 凹陷 | 硬滑 | 是 |
| 2 | 乌黑 | 蜷缩 | 沉闷 | 清晰 | 凹陷 | — | 是 |
| 3 | 乌黑 | 蜷缩 | — | 清晰 | 凹陷 | 硬滑 | 是 |
| 4 | 青绿 | 蜷缩 | 沉闷 | 清晰 | 凹陷 | 硬滑 | 是 |
| 5 | — | 蜷缩 | 浊响 | 清晰 | 凹陷 | 硬滑 | 是 |
| 6 | 青绿 | 稍蜷 | 浊响 | 清晰 | — | 软粘 | 是 |
| 7 | 乌黑 | 稍蜷 | 浊响 | 稍糊 | 稍凹 | 软粘 | 是 |
| 8 | 乌黑 | 稍蜷 | 浊响 | — | 稍凹 | 硬滑 | 是 |
| 9 | 乌黑 | — | 沉闷 | 稍糊 | 稍凹 | 硬滑 | 否 |
| 10 | 青绿 | 硬挺 | 清脆 | — | 平坦 | 软粘 | 否 |
| 11 | 浅白 | 硬挺 | 清脆 | 模糊 | 平坦 | — | 否 |
| 12 | 浅白 | 蜷缩 | — | 模糊 | 平坦 | 软粘 | 否 |
| 13 | — | 稍蜷 | 浊响 | 稍糊 | 凹陷 | 硬滑 | 否 |
| 14 | 浅白 | 稍蜷 | 沉闷 | 稍糊 | 凹陷 | 硬滑 | 否 |
| 15 | 乌黑 | 稍蜷 | 浊响 | 清晰 | — | 软粘 | 否 |
| 16 | 浅白 | 蜷缩 | 浊响 | 模糊 | 平坦 | 硬滑 | 否 |
| 17 | 青绿 | — | 浊响 | 稍糊 | 稍凹 | 硬滑 | 否 |
解:根节点包含样本集 \(D\) 中全部 \(17\) 个样例,各样例的权值为 \(1\)。
以特征 “色泽” 为例,令该特征上无缺失值的样本子集为 \(\tilde{D}\) ,包含的编号为 \(\{2,3,4,6,7,8,9,10,11,12,14,15,16,17\}\) ,共 \(14\) 个,
\(\tilde{D}\) 的信息熵为
令 \(\tilde{D}^1、\tilde{D}^2、\tilde{D}^3\) 表示特征 “色泽” 的取值 “青绿”,“乌黑”,“浅白”,
因此,样本子集 \(\tilde{D}\) 上特征 “色泽” 的信息增益为
样本集 \(D\) 上特征 “色泽” 的信息增益为
同理
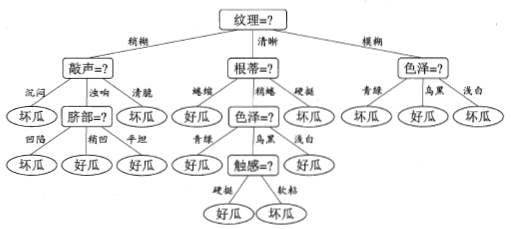
"纹理" 在所有特征中信息增益最大,用于对根结点进行划分。
划分结果使编号为 \(\{1,2,3,4,5,6,15\}\) 的样本进入 “纹理=清晰” 分支;
编号为 \(\{7,9,13,14,17\}\) 的样本进入 “纹理=稍糊” 分支;
编号为 \(\{11,12,16\}\) 的样本进入 “纹理=模糊” 分支,且样本在各子结点中的权重保持为1。
而编号为 \(\{8\}\) 的样本在特征 “纹理” 上出现缺失,因此它将同时进入三个分支汇总,权重在三个子结点中分别为 \(\frac{7}{15}、\frac{5}{15}、\frac{3}{15}\),编号为 \(\{10\}\) 同理。
最终生成的决策树:
5. C4.5 的不足
① \(C4.5\) 生成的是多叉树。\(CART\) 决策树是二叉树,二叉树模型比多叉树运算效率高。
② \(C4.5\) 只能用于分类。\(CART\) 即可用于分类,也可用于回归。
③ \(C4.5\) 使用了熵模型,在计算时有大量的对数运算,如果是连续值还有大量排序运算。因此 \(CART\) 用基尼系数代替熵模型。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号