决策树算法简单总结
·来自：https://mp.weixin.qq.com/s/tevVm0jlS6vZ3LCnczWD0w
前言
李航老师《统计学习方法》详细的描述了决策树的生成和剪枝。根据书的内容，做总结如下。
目录
- 决策树不确定性的度量方法
- 决策树的特征筛选准则
- 决策函数的损失函数评估
- 决策树最优模型的构建步骤
- 决策树的优缺点分析
a. 决策树不确定性的度量方法
1. 不确定性理解
下图为事件A是否发生的概率分布，事件发生记为1，讨论事件A的不确定性。
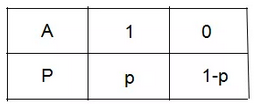
（1）一种极端情况，若p=1或p=0，表示为事件A必定发生或事件A不可能发生。
（2）若p>1/2，即事件A发生的概率大于事件A不发生的概率，我们倾向于预测事件A是发生的；若 p<1/2，即事件A不发生的概率小于事件A发生的概率，我们倾向于预测事件A是不发生的；若 p=1/2，即事件A发生的概率等于事件A不发生的概率，我们无法作出预测。
2. 决策树不确定性的度量方法
这里用熵和基尼指数去衡量数据集的不确定性，假设数据集包含K类，每个类的大小和比例分别为Di和pi，i = 1，2，...，k。
（1）熵的不确定性度量方法
信息论和概率统计中，熵是表示随机变量不确定性的度量，令熵为H(p)，则：
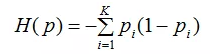
熵越大，数据集的不确定性就越大。
（2）基尼指数的不确定度量方法
数据集的基尼指数定义为：
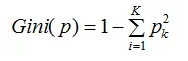
基尼指数越大，数据集不确定性越大。
b. 决策树特征筛选准则
假设数据集A共有K个特征，记为xi，i = 1,2,...,K。数据集A的不确定性越大，则数据集A包含的信息越多。假设数据集A的信息为H(A)，经过特征xi筛选后的信息为H(A|xi)，定义信息增益g(A, xi)为两者的差值，即：
g(A, xi) = H(A) - H(A|xi)
选择使数据集A信息增益最大的特征作为决策树当前节点，数学表示为：
x = max( g(A,xi) ) = max( H(A) - H(A|xi) )
C. 决策树的损失函数评估
令决策树的叶节点数为T，损失函数为：
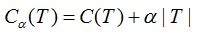
其中C(T)为决策树的训练误差，决策树模型用不确定性表示，不确定性越大，则训练误差亦越大。T表示决策树的复杂度惩罚，α参数权衡训练数据的训练误差与模型复杂度的关系，意义相当于正则化参数。
考虑极端情况：当α趋于0的时候，最优决策树模型的训练误差接近 0，模型处于过拟合；当α趋于无穷大的时候，最优决策树模型是由根节点组成的单节点树。
d. 决策树最优模型的构建步骤
将数据集A通过一定的比例划分为训练集和测试集。
决策树的损失函数：
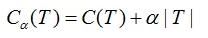
决策树最优模型的构建步骤包括训练阶段和测试阶段：
训练阶段：
（1）最小化决策树的不确定性值得到的生成模型，即决策树生成；
（2）通过决策树剪枝，得到不同的正则化参数α下的最优决策树模型，即决策树剪枝。
下面重点讨论训练阶段的决策树生成步骤和决策树剪枝步骤。
决策树生成步骤：
（1） 根据决策树的特征筛选准则，选择数据集信息增益最大的特征；
（2） 重复第一个步骤，直到所有叶节点的不确定性为0 。
决策树剪枝步骤：
（1）将正则化参数α从小到大分成不同的区间
e. 决策树优缺点
优点：模型很强的解释性
缺点：容易过拟合。即训练误差很小，测试误差很大。为避免过拟合，使用时结合集成算法。如：bagging算法、boosting算法。
