正则化方法小结
来自：https://mp.weixin.qq.com/s/CDMBQPgzcrjbZ_sX01q2hQ
在算法中使用正则化的目的是防止模型出现过拟合。
提到正则化，想到L1范数和L2范数。在这之前，先看LP范数是什么。
LP范数
范数简单理解为向量空间中的距离，距离定义很抽象，只要满足非负、自反、三角不等式就可以称之为距离。
LP范数不是一个范数，而是一组范数，定义为：
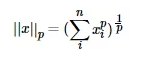
p的范围[1， +∞]。p在（0,1）范围内定义的并不是范数，因为违反了三角不等式。
根据p的变化，范数也有着不同的变化，借用一个经典的有关p范数的变化图如下：
上图表示了p在（0，+∞）变化时，单位球（unit ball）的变化情况。
在p范数下定义的单位球都是凸集，但是当0<p<1时，该定义下的单位球不是凸集（0<p<1不是范数）。
剩下当p = 0时，即L0范数啥玩意？
L0范数表示向量中非0元素的个数，公式表示如下：
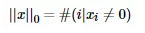
我们可以通过最小化L0范数，来寻找最少最优的稀疏特征项。但不幸的是，L0范数的最优化问题是一个NP-hard问题（L0范数是非凸的）。因此，在实际应用中我们经常对L0进行凸松弛，理论上有证明，L1范数是L0范数的最优凸近似，因此通常使用L1范数来代替优化L0范数。
L1范数
L1范数就是当p = 1时，数学形式：
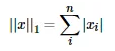
通过上式得出，L1范数就是向量各元素的绝对值之和，也被称为是“稀疏规则算子”（Lassoregularization）。
那么问题来了，为什么稀疏化？
最直接的两个：
- 特征选择
- 可解释性
L2范数
L2范数就是欧几里得距离，公式：
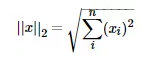
L2范数有很多名称，有人把它的回归叫“岭回归”（Ridge Regression），也有人叫它“权值衰减”（Weight Decay）。以L2范数作为正则项可以得到稠密解，即每个特征对应的参数w都很小，接近于0但是不为0；此外，L2范数作为正则化项，可以防止模型为了迎合训练集而过于复杂造成过拟合的情况，从而提高模型的泛化能力。
L1范数与L2范数的区别
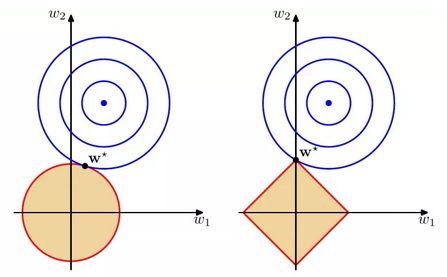
如图，蓝色圆圈表示问题可能的解范围，橘色圆圈表示正则项可能的解范围。而整个目标函数（原问题+正则项）有解当且仅当两个解范围相切。从图看出，由于L2范数解范围是圆，所以相切的点有很大可能不在坐标轴上，而由于L1范数是菱形（顶点是凸出来的），其相切的点更可能在坐标轴上，而坐标轴上的点有一个特点，其只有一个坐标分量不为0，其他坐标分量为0，即稀疏的。所以有如下结论，L1范数可以导致稀疏解，L2范数导致稠密解。
从贝叶斯先验的角度看，当训练一个模型时，仅依靠当前的训练数据集是不够的，为了实现更好的泛化能力，往往需要加入先验项，而加入正则项相当于加入了一种先验。
- L1范数相当于加入了一个Laplacean先验。
- L2范数相当于加入了一个Gaussian先验。
更详细的L1范数和L2范数区别，点击《L1和L2正则化解释》
