偏度与峰度的正态性分布判断
偏度与峰度的正态性分布判断
用统计方法对数据进行分析，有很多方法如T检验、方差分析、相关分析以及线性回归等。都要求数据服从正态分布或近似正态分布。上篇博客用Q-Q图验证数据集符合正态分布。这篇博客先介绍偏度与峰度定义，然后用偏度与峰度检测数据集是否符合正态分布，最后分析该检测算法的使用条件以及spss的结果分析。
1、偏度与峰度
（1）偏度（Skewness）
偏度的衡量是相对于正态分布来说，正态分布的偏度为0，即若数据分布是对称的，偏度为0。偏度大于0，则分布偏右，即分布有一条长尾在右；偏度小于0，则分布偏左，即分布有一条长尾在左；
同时偏度的绝对值越大，说明分布的偏移程度越严重。
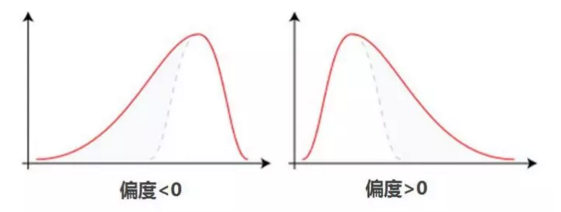
注意：数据分布的左偏或右偏，指的是数值拖尾的方向，而不是峰的位置。
（2）峰度(Kurtosis)
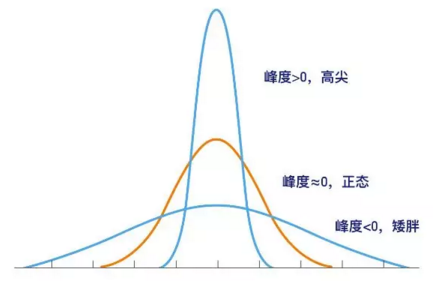
峰度，是研究数据分布陡峭或平滑的统计量，通过对峰度系数的测量，判定数据相对于正态分布而言是平缓还是陡峭。比如正态分布的峰度为0，均匀分布的峰度为-1.2（平缓），指数分布的峰度为6（陡峭）。
峰度≈0，分布服从正态分布；
峰度>0，分布陡峭；
峰度<0，分布平缓；
2、正态性检验
计算偏度和峰度的Z评分（Z-score）。
偏度Z-score = 偏度值 ÷偏度值的标准差
峰度Z-score = 峰度值 ÷峰度值的标准差
在α=0.05的检验水平下，偏度Z-score和峰度Z-score是否满足假设条件所限制的变量范围，若都满足则可认为服从正态分布，若一个不满足则认为不服从正态分布。
3、正态性检验的适用条件
样本的增加会减小偏度值和峰度值的标准差，相应的Z-score会变大，最终会拒绝条件假设，会给正确判断样本数据的正态性情况造成一定的干扰。因此，当样本量小于100时，用偏度和峰度来判断样本的正态分布性比较合理。
4、 SPSS结果分析
峰度Z-score = 5.166/0.425 > Z(α)，α=0.05；因此该特征不符合正态分布。
