聊一聊极大似然估计
本文作者Key,博客园主页:https://home.cnblogs.com/u/key1994/
本内容为个人原创作品,转载请注明出处或联系:zhengzha16@163.com
1.Introduction
极大似然估计(Maximum Likelihood Estimation,MLE),也可翻译为最大似然估计,在理解这个算法之前我们先从名称上试着分析一下。
首先,MLE的本质是一种估计方法。估计在我们的生活中无处不在,估计方法更是数不胜数,那么为什么要估计呢?我觉得无非以下两个原因:
无法获得准确的值。例如你去菜市场买菜,一颗白菜重6两,那么这个数字就是估计得到的。因为不管用传统的秤还是电子秤,都是存在误差的,所以“6两”这个数字一定是不准确的,只是误差在我们的允许范围之内而已。当然,我们可以将这颗白菜拿到专业的实验室,采用全世界最先进最准确的天平来称重,这无异于高射炮打蚊子。
所以,第二个要进行估算的原因是得到准确的值成本太高。如果对全国人口进行普查,理论上来讲是可以得到全中国的实际人口数量的,因为人是个体,即一个活体是否应该被统计为人的概率要么为0,要么为1,不存在其他情况。但是,全中国有十几亿人口,我们要求人口普查结果100%精确,一个不多一个不少,真的有意义吗?
以上是对两种结果的直观描述。当然,放到科学领域这样的示例依然不胜枚举。而极大似然估计要解决什么问题呢?
考虑这样一种情况,对于某一数学问题,我们已经建立了其数学模型,但是模型参数无法准确获得,我们肯定要想办法去确定这些参数。我们能做的就是获得n个样本,然后基于这些样本来推测模型参数的最大可能取值。这就是极大似然估计的基本原理。
这里的似然,英文为likelihood,可以理解为可能性,所以极大似然估计方法是一种基于某事件最有可能发生而推导出的算法。通过这种顾名思义式的理解,可以帮助我们了解极大似然估计算法的原理。
2.公式推导
假设我们已经通过实验获得了n个样本,分别为x1,x2,…,xn,模型参数为q,这里的q可以是一个数值,也可以是由一组数值组成的向量,具体情况视数学模型而定。
我们可以选取𝜃'(𝑥1,𝑥2,..,𝑥𝑛) 作为 𝜃 的估计值,使得当 𝜃= (𝑥1,𝑥2,..,𝑥𝑛) 时,样本出现的概率最大。由于𝜃的求解需要以样本(𝑥1,𝑥2,..,𝑥𝑛)为基础,所以这里𝜃'看作是关于样本(𝑥1,𝑥2,..,𝑥𝑛)的函数。
以离散型随机变量为例:
假设分布律为 𝑃{𝑋=𝑥}=𝑝(𝑥;𝜃) ,𝜃 为待估计参数,𝑝(𝑥;𝜃) 表示估计参数为 𝜃 时,发生 𝑥 的概率。那么当样本值为(𝑥1,𝑥2,..,𝑥𝑛)时,
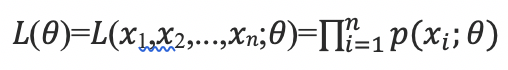
其中 𝐿(𝜃) 称为样本的似然函数。𝐿(𝑥1,𝑥2,...,𝑥𝑛;𝜃)表示当模型参数为𝜃时,样本(𝑥1,𝑥2,..,𝑥𝑛)同时出现的概率。由于这里假设每次实验过程是独立的,因此𝐿(𝑥1,𝑥2,...,𝑥𝑛;𝜃)的值等于当模型参数为𝜃时每个样本发生概率的乘积。
若满足:
𝐿(𝑥1,𝑥2,..,𝑥𝑛; )=𝑚𝑎𝑥𝜃𝐿(𝑥1,𝑥2,..,𝑥𝑛;𝜃)
也就是说,当参数 𝜃= 𝜃' 时,似然函数可以取最大值,那么 𝜃'就叫做参数 𝜃 的极大似然估计值。
极大似然估计的核心正在于此,这句话该怎么理解呢?
假设𝜃= 𝜃',也就是说在模型参数取得真值时,样本(𝑥1,𝑥2,..,𝑥𝑛)同时出现的概率最大,因为样本的采样就是基于真实模型来采样的。所以极大似然估计算法可以这样理解:当基于模型参数估计值计算出采样样本(𝑥1,𝑥2,..,𝑥𝑛)同时发生的概率最大时,模型参数估计值与真实值匹配的可能性也最大。(这个地方有点拗口,关键是要读者自己理解)
若想计算𝜃的最优解,只需令似然函数对每个模型参数的偏导值为0然后求解即可。
需要注意的是,在实际的计算中,往往将似然函数采用对数的形式来表示,这样做的目的是为了防止计算机在运算过程中产生下溢。什么是下溢呢?就是计算机为了计算方便,往往将较小的数值近似为0来计算,这样整个似然函数的值恒为0。采用对数来计算可以将乘法运算转换为加法运算,从而避免下溢的发生。



