拉格朗日乘子法+KKT条件

算法原理

拉格朗日乘子法

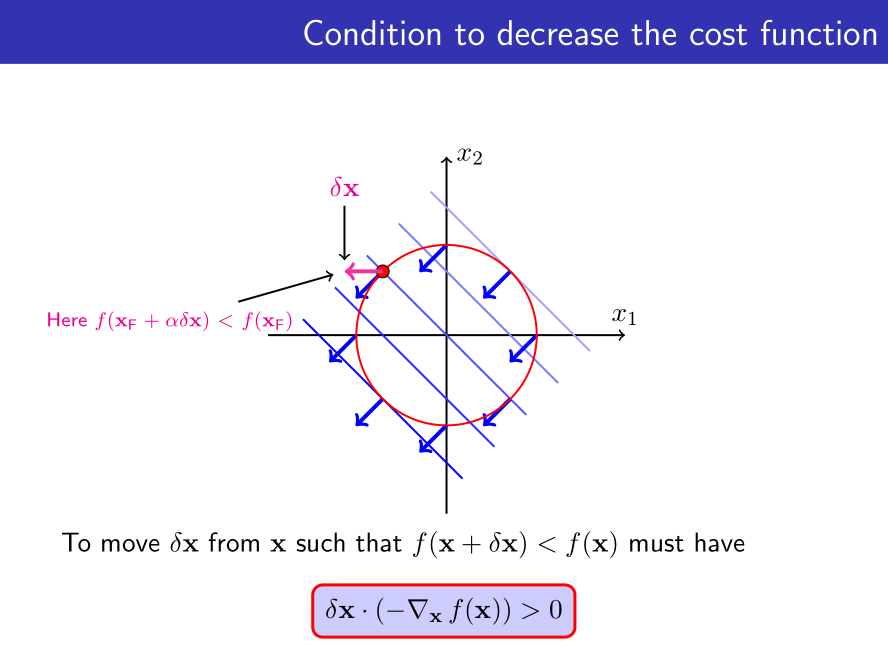
为保证随机选取的点走向min的地方,方向应该和f(x)的梯度方向夹角小于90°

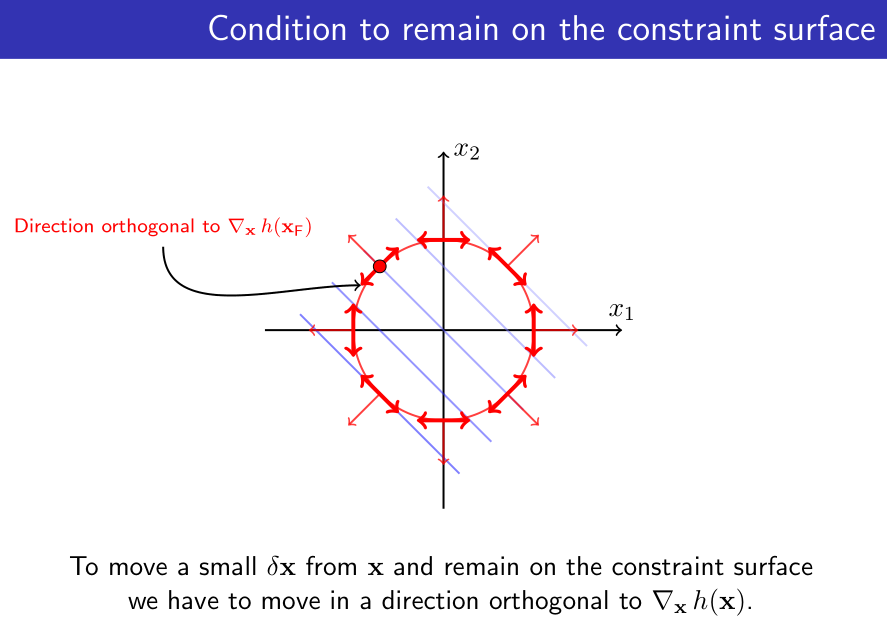
为保证点仍在约束域上

在局部极值点上,f(x)和h(x)相同梯度,μ是两者之间的比例

h(x)的梯度符号任意选择都行,第三条是保证凸函数

KKT条件

用来解决约束条件中含有不等式的情况

如果局部最优正好等于全局最优

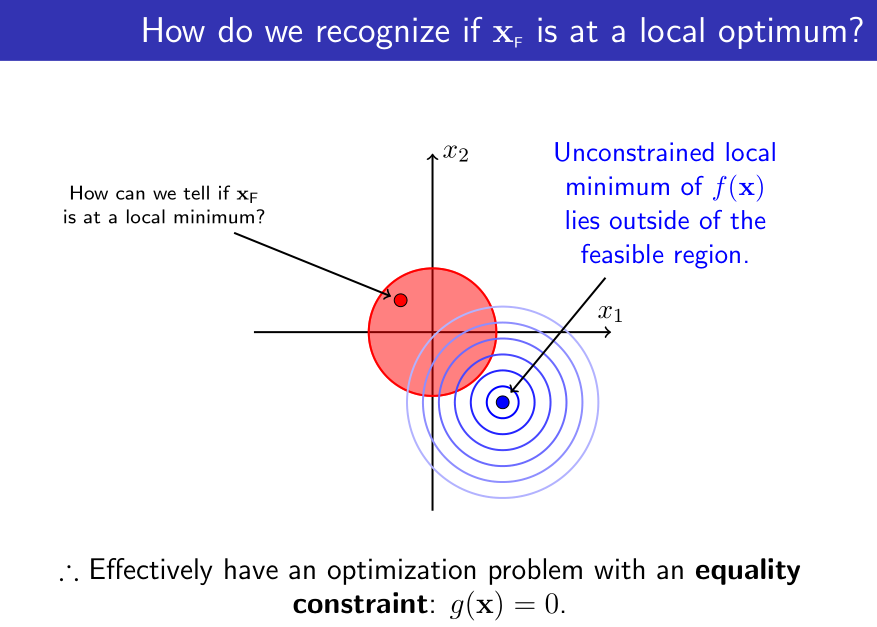
当全局最优不在约束条件内时

注意满足条件的不一定是局部最小

把上面的总结一下


[注]:条件3的使用情形是,λ>0,保证了g(x)=0,即此时在边界条件上取得极值

参考文献

http://www.csc.kth.se/utbildning/kth/kurser/DD3364/Lectures/KKT.pdf