最优间隔分类器

最优间隔分类器

1. 最优间隔分类器

对于一个给定的数据集，目前有一个很现实的需求就是要找到一个合适的决策边界，使得样本中的最小间隔(几何间隔)最大，而且这样的分类器能够使得分割的训练样本集之间的间隔(gap)最大。现在，我们假设训练集合线性可分，即可以找一条超平面把正样本和负样本分割开来。那么我们如何找到一个超平面来最大化几何间隔呢？我们得到了如下的优化问题：

max_γ,w,b γ

s.t. y⁽ⁱ⁾(w^Tx⁽ⁱ⁾+ b) ≥ γ, i = 1, . . . , m

||w|| = 1

也就是说，我们希望最大化γ，其中对于每一个样本而言，每一个函数间隔值都不小于γ。其中，设定||w|| 固定为 1，能够保证函数间隔等于几何间隔，也能保证几何间隔最小可达到γ。因此，解决这个优化问题后就可以得到该训练集合的最大可能几何间隔。

但是很难解决上面的优化问题，因为||w|| = 1是非凸优化，这就无法使用标准优化软件去解决这个优化问题。因此，我们把这个优化问题转化成相对简单的问题，如下：

max_γ,w,b ˆγ/||w||

s.t. y⁽ⁱ⁾(w^Tx⁽ⁱ⁾+ b) ≥ ˆγ, i = 1, . . . , m

这里我们将要最大化ˆγ/||w||，约束条件是函数间隔最小达到ˆγ。因为几何间隔和函数间隔存在关系γ = ˆγ/||w||，这将给我们想要的答案。此外，我们也摆脱了||w|| = 1的限制。但是依然存在的问题是我们要最优化的ˆγ/||w||仍然是一个非凸函数，也就是说我们仍然不能通过常规的优化软件进行优化。

回想一下之前的讨论，我们通过缩放w和b的值并不影响最终的结果，这一点很关键。我们将通过介绍如何去缩放wb，使得训练集合的函数间隔一定是1，即ˆγ = 1。因此w和b乘以一个常数之后，得到的函数间隔也会相应的乘以该常数。这是一个比例约束，可以通过缩放wb来满足。把这一点加入我们上面的优化问题，可以得到最大化ˆγ/||w|| = 1 / ||w|| 与最小化||w||² 是一样的效果(这里已经没有了 ||w|| = 1的限制)。因此，我们得到了如下的优化问题：

min_γ,_w,b ½ * ||w||²

s.t. y⁽ⁱ⁾(w^Tx⁽ⁱ⁾+ b) ≥ 1, i = 1, . . . , m

我们现在已经把之前的问题转化成一个相对容易解决的问题了。上面的优化是一个凸二次优化问题，而且是线性约束。该结果给出的是最优化间隔分类器。此外，该优化问题可以用商业二次规划(quadratic programming，程序)程序来求解。

在解决这个优化问题之前，我们插入一段关于拉格朗日对偶(Lagrange duality)的介绍。这将使我们进入优化问题的对偶形式，这在后面提到的用核方法来优化最大间隔分类器中起到很重要的作用，能够使该分类器在高维数据中更有效率的工作。此外，对偶形式能够使我们比普通的QP代码更有效率的解决上面的优化问题。

1. 拉格朗日对偶

我们先把SVM和最大间隔分类放在一边，这里主要讨论一下如何求解约束优化问题。考虑如下形式的问题：

min_w f (w)

s.t. h_i(w) = 0, i = 1, . . . , l.

在这里我们将介绍拉格朗日乘子法(Lagrange multipliers)。在该方法中，我们定义拉格朗日算符(Lagrangian)如下：

L(w, β) = f (w) +

这里的β_i称之为拉格朗日乘子(Lagrange multipliers)。求解该式的最优解，只需要使得L对 β_i 和w_i 的偏微分为0即可，如下：

；

之后只要求解出w和 β 即可。

在这部分，我们将把这个问题扩展到约束优化问题中，即找到约束优化中不等式来代替拉格朗日乘子法中的等式约束。这里不再讲解拉格朗日对偶理论和详细的证明，但是仍将给出主要的方法和结果，以便我们能够把该方法应用到最优间隔分类器的优化问题上。

考虑如下问题，我们称之为原始优化问题(primal optimization problem)：

min_w f (w)

s.t. g_i(w) ≤ 0, i = 1, . . . , k

h_i(w) = 0, i = 1, . . . , l.

为了解决该问题，我们开始定义广义拉格朗日(generalized Lagrangian)：

L(w, α, β) = f (w) + +

这里，α_i 和 β_i都是拉格朗日乘子。考虑下式：

θ_P(w) = max_{α,β : αi≥0} L(w, α, β)

这里下标P表示原始的(primal)。现在我们赋一些值给w。如果w违反了原始限制(如对于某些i，g_i(w) > 0 或者 h_i(w) ！= 0)，那么我们将得到：

θ_P(w) = max f (w) + + = ∞

相反的，如果对于某个w，约束条件能够很好的满足，那么θ_P(w) = f(w)，因此有：

θ_P(w) =

因此，对于所有满足原始约束条件的w，θ_P取得相同的值作为我们问题的目标。如果不满足约束条件，则θ_P结果为正无穷大。因此，考虑最小优化问题：

min_w θ_P(w) = min_w max_{α,β : αi≥0} L(w, α, β)

我们可以看到这和原始优化问题是相同(具有相同的解)。为了后面的使用，我们定义最优目标值为p^∗= min_w θ_P(w) ,称之为原始问题解。

现在我们考虑一个稍微不同的问题，定义θ_D(α, β) = min_w L(w, α, β)，这里的下标D表示对偶(dual)。注意这里与θ_P不同，θ_P是针对α, β的最优化函数，而θ_D是针对w的最优化函数。现在，我们可以得到对偶优化问题：

max_{α,β:αi ≥0} θ_D(α, β) = max_{α,β:αi ≥0} min_w L(w, α, β)

这恰好和原始问题一样，只是我们改变了最大化和最小化的顺序。我们定义该对偶问题的最优化值为d^∗= max_{α,β : αi ≥0} θ_D(w)。那么原始问题和该对偶问题有什么联系呢？很容易看出：d^∗= max_{α,β:αi ≥0} min_w L(w, α, β) ≤ min_w max_{α,β:αi≥0} L(w, α, β) = p^∗

当然，在某些情况下，存在d^∗= p^∗ 。因此，我们可以通过解决对偶问题替换原始问题。我们来看看能够替代的情况有哪些。

假设f和g是凸函数，而且h_i是仿射(Affine，类似于线性，但是允许截距项的存在)函数。此外，我们认为g_i是可行的，即对于所有的i，存在w使得gi(w)<0 。针对该假设，一定存在w∗, α∗, β∗使得w∗为原始问题的解， α∗, β∗是对偶问题的解，而且p^∗= d^∗= L(w^∗, α^∗, β^∗)。此外，w^∗, α^∗, β^∗还满足KKT条件(Karush-Kuhn-Tucker)，如下所示。

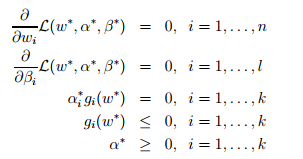
此外，如果存在w^∗, α^∗, β^∗满足KKT条件，那么这也是原始问题和对偶问题的解。对于条件中α^∗_ig_i(w^∗) = 0, i=1, ... ,k，称之为KKT对偶互补条件(dual complementarity condition)。特别的，这里暗含着如果α^∗_i>0，那么g_i(w^∗) =0。之后，这在SVM中的支持向量(support vectors)起到关键作用。此外，KKT对偶互补条件也将在我们SMO的收敛测试中用到。

1. 最优间隔分类器

之前我们讨论了如下优化问题(即原始优化问题)来求得最优间隔分类器。

min_γ,_w,b ½ * ||w||²

s.t. y⁽ⁱ⁾(w^Tx⁽ⁱ⁾+ b) ≥ 1, i = 1, . . . , m

我们可以把约束条件表示成如下形式：

g_i(w) = −y⁽ⁱ⁾(w^Tx⁽ⁱ⁾+ b) + 1 ≤ 0

针对每一个样本，我们都存在该约束条件。根据KKT对偶互补条件α_ig_i(w) = 0，我们知道仅对于训练集合中函数间隔恰好等于1的样本，才存在线性约束前面的系数α_i > 0，也就是说这些约束式g_i(w) = 0。对于其他不在线上的点(g_i(w)<0),极值不会在他们所在的范围内取得，α_i = 0。

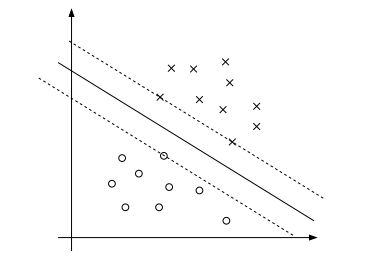
看下面的图：实线是最大间隔超平面，假设×号的是正例，圆圈的是负例。在虚线上的点就是函数间隔是1的点，那么他们前面的系数α_i > 0，其他点都是α_i = 0。这三个点称作支持向量。一般而言，支持向量数量相对于整个训练集合而言是非常少的，之后我们会发现这是非常有用的。

    之后，得到了我们优化问题的拉格朗日形式，如下：

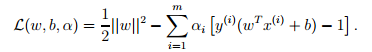
注意到这里只有α_i和β_i ，因为原问题中没有等式约束，只有不等式约束。接下来我们需要寻找该问题的对偶式。首先，对于给定的α_i，L(w, b, α)仅受w和b影响，我们需要最小化L(w, b, α)，只需要让L对w和b的偏微分为0。对w求偏微分如下：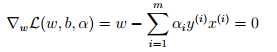

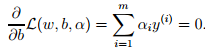
由此得到w = ，之后对b求偏微分得到：

我们把得到的w值带回到构造的拉格朗日函数中，化简如下：

由于 = 0，因此最终得到：

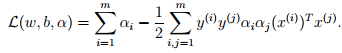
这里我们把向量内积 (x⁽ⁱ⁾)^Tx^(j) 表示为<(x⁽ⁱ⁾), x^(j)>。此时的拉格朗日函数只包涵了变量α_i，求解出α_i之后即可以得到w和b。根据对偶问题的求解，我们得到了如下的最大化问题：

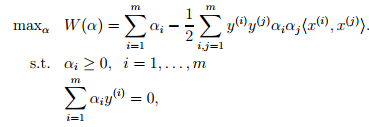
这里我们需要考虑p^∗ = d^∗ 的条件，即KKT条件。因为目标函数和线性约束都是凸函数，而这里不存在等式约束h，存在w使得对于所有的i，使得g_i(w) <= 0，因此存在w^* 和 a^*使得w^*是原问题的解， a^*是对偶问题的解。这里求解的a_i就a^*如果求解出了a_i，根据w = 即可以求解出w(也就是w^*，原问题的解)。同样根据下式得到b：

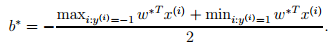
求解得到b，即距离超平面最近的正的函数间隔要等于距离超平面最近的负的函数距离。关于上面的对偶问题如何求解，在下一讲中我们将采用SMO算法来阐明。

此外，我们额外考虑一下w的求解公式。假设我们已经通过训练集合得到了模型的各个参数，现在要预测一个新的输入x，我们需要计算w^T+b ，如果得到的值大于0，那么y=1。这里我们把w = 考虑进去，得到如下结果，

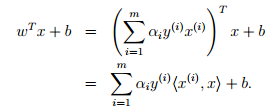
由此可以看出，与之前计算w^T+b不同，这里只要计算新的样本和训练样本的内积即可。当然，从前面的KKT条件中知道，只有支持向量的a_i > 0，其他情况a_i = 0，其他情况下a_i=0。因此，我们只需要进算新的样本和支持向量的内积就可以。

通过优化问题的对偶形式，我们更深入的看到了需要优化问题的结构，并且找到了能够适合于特征向量内积的算法。在下一讲，我们会讨论核方法在高维数据中使用以及求解支持向量机的算法。