变分例子

接着主要讲几个变分推断的例子，试图阐述清楚变分推断到底是如何应用的。首先是二元高斯分布的近似。我们假设二元高斯分布是可分解的，也就是两变量之间独立。
二元高斯分布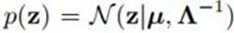
其中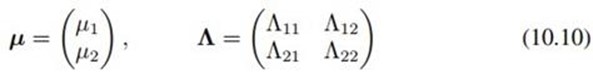

可分解形式为：
我们想用q(z)去近似p(z)，用前面推导出来的(10.9)：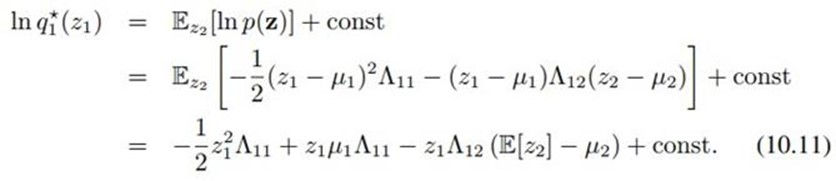

因为是求z1的分布，所以按(10.9)，我们在z2上求期望，得到(10.11)。然后，我们就可以祭出第二章修炼的法宝——配方法，从(10.11)得到高斯分布：

其中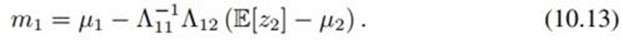

同样，z2的分布也可如法炮制：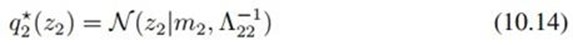

其中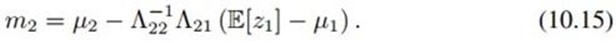

它们是完全对称的。因为m1里有z2的期望，而m2里又有z1的期望，所以我们可以设一个初始值，然后迭代求解。但实际上这两个式子恰好有解析解：和，我们可把它们代入(10.13)和(10.15)验证一下。
下面我们重点看一下参数推断问题，但其核心思想实际上和前面讲的例子区别不大。同样还是先看一下高斯分布：
我们想推断后验高斯分布的均值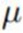和精度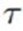
假如我们观察到N个数据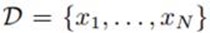，那么似然函数就是：

另外引入先验分布，均值服从高斯分布、精度服从Gamma分布：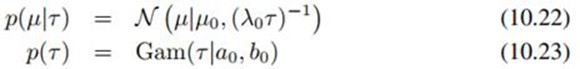

其实这个问题我们前面第二章就讲过，不用变分推断也能直接求出来，但这里用变分推断实际上增加了更多的灵活性，因为如果先验和似然的形式不是高斯-Gamma的形式，而是更加复杂，那么我们也可以利用变分推断来算参数，这是非常方便的。我们这里只是用我们熟悉的高斯分布来举例子，把这个弄明白，以后再推广到其他例子上就容易多了。
利用mean field形式(10.9)，我们可计算出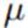的分布：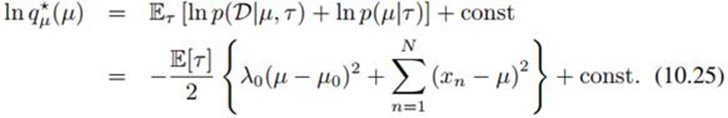

可以看到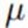，服从高斯分布形式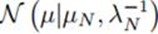，且通过配方，可得到该分布参数为：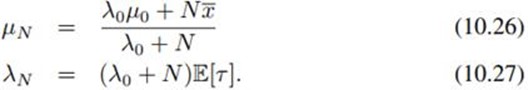

注意到，样本越多也就是N越大时，均值会趋向于样本均值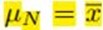，同时精度趋向于无穷大。同样可用(10.9)计算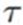的分布，得到：

它服从Gamma分布形式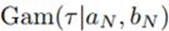，可以看到，(10.27)和(10.30)里，仍然有和另一分布相关的期望需要计算，所以我们可以设定初始值，然后迭代计算。迭代过程和收敛后的结果图书上10.4所示：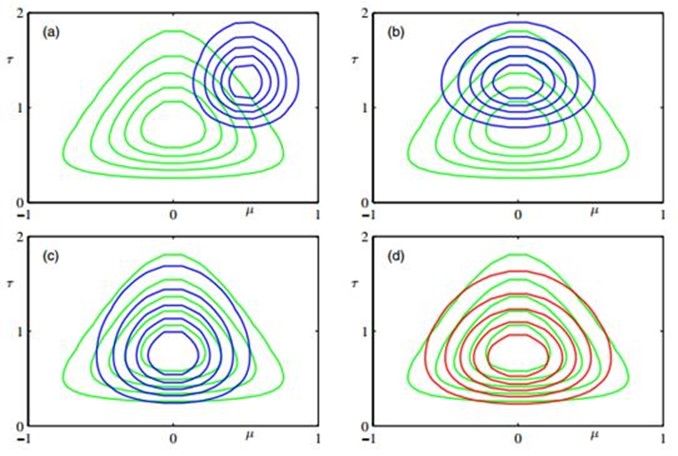

再看一个例子，是用变分推断计算线性回归的参数。线性回归的参数w，有似然和先验如下：

2.3.6讲过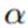，的共轭先验是Gamma分布：

这样联合分布就是：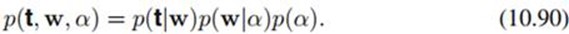

其概率图模型为图10.8：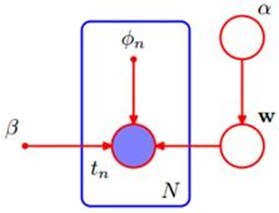

利用变分推断来计算w和，同样是假设它们有可分解形式：

再用(10.9)（这个绝对是看家法宝）来搞，得到：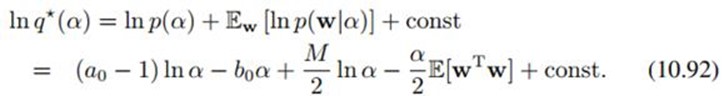

可看到它服从Gamma分布：

其中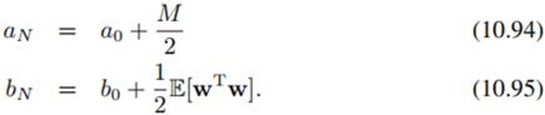

以及：
 

可看到它服从高斯分布：

其中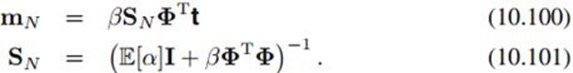

(10.95)和(10.97)里还有奇怪的东西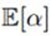和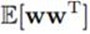，从附录B可知，它们分别是：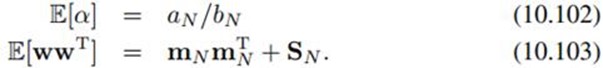

所以我们仍然可以迭代计算：给初始值，每一步都算出a_N、b_N和m_N、S_N，代入求解