变分
变分
概率推断的核心任务就是计算某分布下的的某个函数的期望,或者计算边缘概率分布,条件概率分布等等。EM算法就是计算对数似然函数在隐变量后验分布下的期望。这些任务往往需要积分或求和操作。但在很多情况下,计算这些东西往往不那么容易。首先,积分中涉及的分布可能有很复杂的形式,这样就无法直接得到解析解。其次,我们要积分的变量空间可能有很高的维度。因为这两个原因,我们进行精确计算往往不可行的。为了解决这一问题,需要引入一些近似计算方法。近似计算有随机和确定两条路子。随机方法就是MCMC之类的采样方法,而确定近似法就是变分这一类方法。变分法的有点主要有:有解析解,计算开销较小,易于在大规模问题中应用。缺点是推导出想要的形式比较困难。也就是人琢磨的部分比较复杂,而机器算得部分比较简单。这和采样刚好相反。
变分的原始目标的是,需要根据已有数据推断需要的分布p;当p不容易表达,不能直接求解时,可尝试使用变分推断的方法,即,寻找容易表达求解的分布q,当q和p的差距很小的时候,q就可以作为p的近似分布,成为输出结果了。
在这个过程中,我们的关键点,从"求分布"的推断问题,变成了"缩小距离"的优化问题。

黄色的分布是我们的原始目标p,不好求。它看上去有点像高斯,那我们尝试从高斯分布中找到一个红q的一个绿q,分别计算一下p和他们之间的距离,选更像p的q作为p的近似分布。
变分推断的步骤:
-
我们拥有两部分输入:数据x,模型p(z, x)。
-
我们需要推断的是后验概率p(z | x),但不能直接求。
-
构造后验概率p(z | x)的近似分布q(z; v)。
-
不断缩小q和p之间的距离直至收敛。
转化成优化问题:
KL散度KL(q||p)
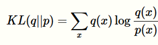
在信息论中,该函数是用来衡量两个分布之间的不同,描述估计分布与真实分布的差别。
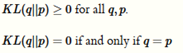
注意
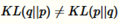
KL散度是非对称的,这也是为什么我们说它是散度而不是距离。
变量的下界
无向图的联合概率分布可以表示成
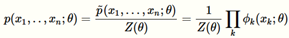

:表示因子
:表示归一化因子
Cliques:集合内的点两两之间有边相连接,这些集合被称为Cliques
C表示cliques的集合
如果知道了联合概率分布就可以知道任何我们想要知道的概率分布,比如条件分布等。
通过这个式子,来优化KL(q||p)是不可能的因为归一化因子,事实上计算KL(q||p)也是不可能的,因为我们需要计算p(x)的概率
因为我们将会使用如下的目标函数,给目标函数和KL散度有相同的表达式,只是将概率P的归一化因子去掉
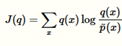
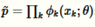
这个方程不是不可计算,它有如下重要的属性:
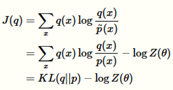
因为
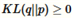
我们可以重新调整这些项
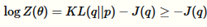
因此-J(q)是配分函数的下界。在很多情况下有很多有意思的解释。例如,
我们可能计算边界概率分布
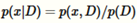
X在给定观测到的数据集D时的概率,我们假设p(x,D)已经可以直接计算,在这个例子中最小化J(q)相当于最大化对数似然函数log P(D)关于观测到的数据。
因为这个原因,-J(q)被称为lower bound or the evidence lower bound (ELBO),经常被写成如下的形式

平均场推断
Q函数通常取如下形式的表达式
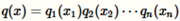
每一个都是一个一维的离散分布,可以通过一张一维表获得
Q函数的这种选择在优化变量的边界的时候是最流行的选择。通过这种函数的变分推断叫做平均场推断。它用来解决如下的优化问题
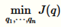
解决这种优化问题的标准方法是通过坐标下降法来完成的的。对于,我们迭代的从j=1,2,3,……,n开始,对于每一个j,我们通过优化KL(q||p)同时保持其他的的坐标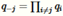 周固定。
周固定。
有趣的是,对于每一个坐标轴的优化有如下简单的表达式来解决


最后因子将会和边缘分布近似
附:
平均场的通俗理解
假设有一个很大很大的教室,里面坐着很多很多的学生,这些学生都在晨读,你是其中的一员。你听到的声音是所有学生发出的声音到拟这个位置的叠加,显然这个求和很复杂,因为你的听觉感受与声源到你的距离有关。为了简化这个求和,我们把所有学生在你这个位置产生的声音效果看作是噪音。如果这个教室真的足够大,大到我们可以忽略边界效应。现在,换一个场景,如果所有学生保持战斗队列(继续晨读),你现在是一位老师,在教室里巡视。然后无论你走到哪里,你的听觉感受都是一样的。这个噪音在任何位置都一样,无论往前走还是往右走一步都一样,这就是平移不变性。这个时候,噪音和一个均匀外场产生的效果一样,这个噪音就是平均场。
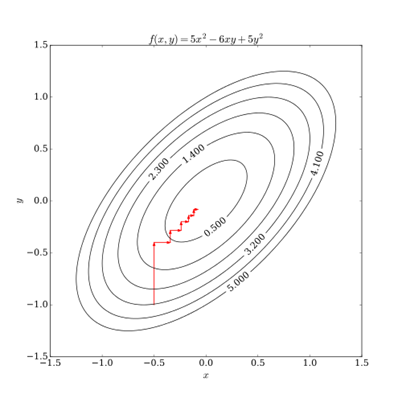
坐标下降法
是一种非梯度优化算法。算法在每次迭代中,在当前点处沿一个坐标方向进行一维搜索以求得一个函数的局部极小值。在整个过程中循环使用不同的坐标方向。对于不可拆分的函数而言,算法可能无法在较小的迭代步数中求得最优解。为了加速收敛,可以采用一个适当的坐标系,例如通过主成分分析获得一个坐标间尽可能不相互关联的新坐标系(参考自适应坐标下降法)。