神经网络及其实现
神经网络及其实现
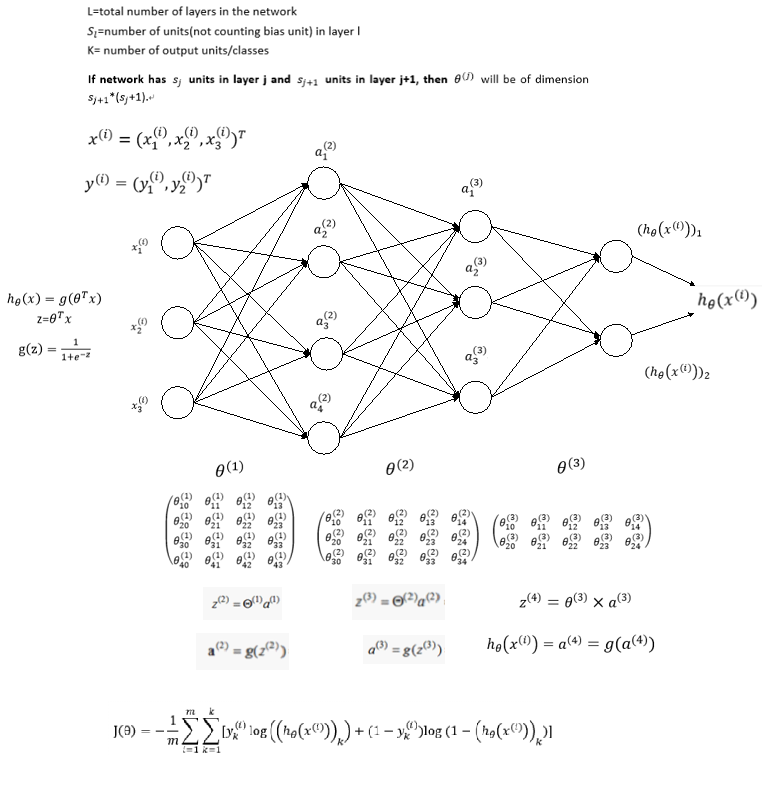
神经网络的表示
最小的神经网络
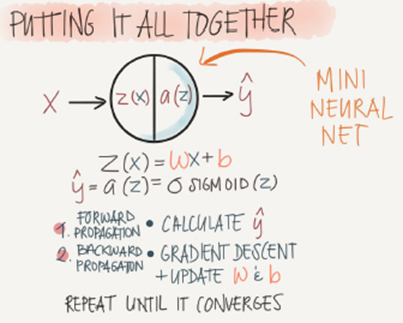
两层神经网络

在下图的表示中将参数b放到了中,每一层增加了一个值为1的隐藏单元

X为输入变量
为权重矩阵(所要计算的参数)
为隐藏层变量
g为激活函数
反向传播算法
下面我们从一个简单的例子入手考虑如何从数学上计算代价函数的梯度,考虑如下简单的神经网络,该神经网络有三层神经元,对应的两个权重矩阵,为了计算梯度我们只需要计算两个偏导数即可:
首先计算第二个权重矩阵的偏导数,即
首先需要在之间建立联系,很容易可以看到的值取决于,而,而又是由取sigmoid得到,最后,所以他们之间的联系可以如下表示:
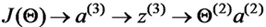
按照求导的链式法则,我们可以先求对的导数,然后乘以对的导数,即
由于
不难计算
令
上式可以重写为
接下来仅需要计算即可,由于
忽略前面的
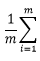
设k=1得到
这里只对一个example推导,最后累加即可
因此
得到下面的求导过程
由于
,计算如下,得
至此我们得到了
接下去我们需要求的偏导数,的依赖关系如下:
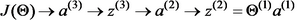
根据链式求导法则有
分别计算等式右边的三项可得
带入后得
令
上式可以重写为
将上面的结果放在一起,我们得到对两个权重矩阵的偏导数为:
观察上面的四个等式,我们发现
-
偏导数可以由当层神经元向量与下一层的误差向量相乘得到
-
当前层的误差向量可以由下一层的误差向量与权重矩阵的乘积得到
所以可以从后往前逐层计算误差向量,然后通过简单的乘法运算得到代价函数对每一层权重矩阵的偏导数。
假设我们有m个训练example,L层神经网络即
初始化:设置(理解为对第l层的权重矩阵的偏导累加值,每一个训练的偏导数累加值,最后再除以样本数得到均值)
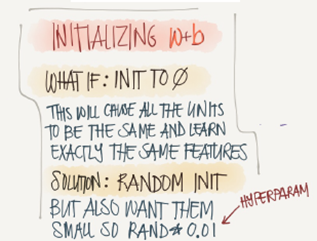
参数w和b的初始化
For k=1:m
设置 =
通过前向传播算法(FP)计算对各层的预测值,其中l=1,2,3,4…,L
计算最后一层的误差向量,利用后向传播算法(BP)从后至前逐层计算误差向量,计算公式为
更新
End//
计算梯度:
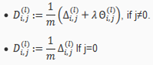
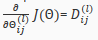
通过梯度下降的方法来更新梯度,从而使代价函数达到最小的目的。
激活函数
上式例子中的激活函数g为SIGMOID
常见的激活函数还有TANH,RELU,LEAKY RELU
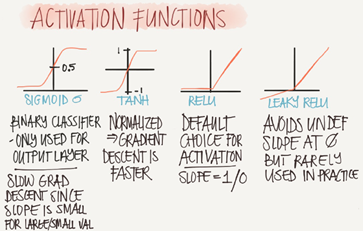
sigmoid激活函数的数学表达式如下
tanh激活函数的数学表达式如下
RELU激活函数
Leak RELU激活函数
注意:神经网络中的激活函数不能为非线性

如果激活函数为线性函数的话,不管你加多少隐藏层,都会和logistic回归一样
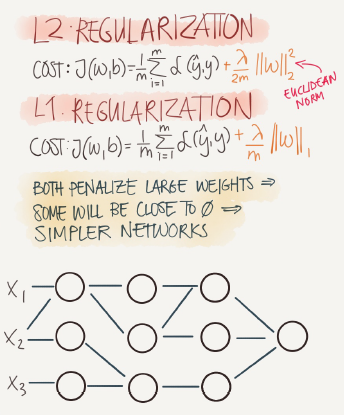
正则化
正则化可以用来帮助神经网络减少方差防止过拟合
常见的正则化有L1,L2
神经网络的matlab实现
sigmoid函数
function g = sigmoid(z)
g = 1.0 ./ (1.0 + exp(-z));
end
sigmoid函数求导
function g = sigmoidGradient(z)
g = zeros(size(z));
g = sigmoid(z) .* (1 - sigmoid(z));
end
初始化权重参数
function W = randInitializeWeights(L_in, L_out)
W = zeros(L_out, 1 + L_in);
epsilon_init = 0.12;
W = rand(L_out, 1 + L_in) * 2 * epsilon_init - epsilon_init;
end
计算代价函数(包含实现了前向传播和反向传播)
function [J grad] = nnCostFunction(nn_params, ...
input_layer_size, ...
hidden_layer_size, ...
num_labels, ...
X, y, lambda)
Theta1 = reshape(nn_params(1:hidden_layer_size * (input_layer_size + 1)),hidden_layer_size, (input_layer_size + 1));
Theta2 = reshape(nn_params((1 + (hidden_layer_size *(input_layer_size + 1))):end),num_labels, (hidden_layer_size + 1));
% Setup some useful variables
m = size(X, 1);
J = 0;
Theta1_grad = zeros(size(Theta1));
Theta2_grad = zeros(size(Theta2));
%% Part 1 前向传播的实现
a1 = [ones(m, 1) X];
z2 = a1 * Theta1';
a2 = sigmoid(z2);
a2 = [ones(size(a2,1), 1) a2];
z3 = a2 * Theta2';
a3 = sigmoid(z3);
hThetaX = a3;
yVec = zeros(m,num_labels);
for i = 1:m
yVec(i,y(i)) = 1;
end
%% 计算代价函数
J = 1/m * sum(sum(-1 * yVec .* log(hThetaX)-(1-yVec) .* log(1-hThetaX)));
%% 正则化项
regularator = (sum(sum(Theta1(:,2:end).^2)) + sum(sum(Theta2(:,2:end).^2))) * (lambda/(2*m));
J = J + regularator;
%% Part 2 反向传播的实现
for t = 1:m
% For the input layer, where l=1:
a1 = [1; X(t,:)'];
% For the hidden layers, where l=2:
z2 = Theta1 * a1;
a2 = [1; sigmoid(z2)];
z3 = Theta2 * a2;
a3 = sigmoid(z3);
yy = ([1:num_labels]==y(t))';
% For the delta values:
delta_3 = a3 - yy;
delta_2 = (Theta2' * delta_3) .* [1; sigmoidGradient(z2)];
delta_2 = delta_2(2:end); % Taking of the bias row
% delta_1 is not calculated because we do not associate error with the input
% Big delta update
Theta1_grad = Theta1_grad + delta_2 * a1';
Theta2_grad = Theta2_grad + delta_3 * a2';
end
Theta1_grad = (1/m) * Theta1_grad + (lambda/m) * [zeros(size(Theta1, 1), 1) Theta1(:,2:end)];
Theta2_grad = (1/m) * Theta2_grad + (lambda/m) * [zeros(size(Theta2, 1), 1) Theta2(:,2:end)];
% Unroll gradients
grad = [Theta1_grad(:) ; Theta2_grad(:)];
end
训练神经网络及预测
%% Initialization
clear ; close all; clc
%% Setup the parameters you will use for this exercise
input_layer_size = 400; % 20x20 Input Images of Digits
hidden_layer_size = 25; % 25 hidden units
num_labels = 10; % 10 labels, from 1 to 10
% (note that we have mapped "0" to label 10)
% 加载训练数据
load('data.mat');
% 初始化权重参数
initial_Theta1 = randInitializeWeights(input_layer_size, hidden_layer_size);
initial_Theta2 = randInitializeWeights(hidden_layer_size, num_labels);
% Unroll parameters
initial_nn_params = [initial_Theta1(:) ; initial_Theta2(:)];
options = optimset('MaxIter', 50);
lambda = 1;
costFunction = @(p) nnCostFunction(p, ...
input_layer_size, ...
hidden_layer_size, ...
num_labels, X, y, lambda);
% 实现迭代计算梯度
[nn_params, cost] = fmincg(costFunction, initial_nn_params, options);
% 获得训练好的权重参数
Theta1 = reshape(nn_params(1:hidden_layer_size * (input_layer_size + 1)),hidden_layer_size, (input_layer_size + 1));
Theta2 = reshape(nn_params((1 + (hidden_layer_size * (input_layer_size + 1))):end), num_labels, (hidden_layer_size + 1));
% 实现预测
pred = predict(Theta1, Theta2, X);
fprintf('\nTraining Set Accuracy: %f\n', mean(double(pred == y)) * 100);

 浙公网安备 33010602011771号
浙公网安备 33010602011771号